Коэффициент жесткости пружины

Вычисляем энергию простого гармонического движения

В простом гармоническом движении периодически происходит увеличение и уменьшение кинетической энергии, например груза на пружине. Ясно, что кинетическая энергия груза не пропадает, а преобразуется в энергию сжатой или растянутой пружины. Эта энергия называется упругой потенциальной энергией пружины. Сколько энергии запасено в сжатой или растянутой пружине?

Попробуем вычислить ее с помощью простых соображений. Как известно, работа ​\( A \)​ силы ​\( F \)​ при перемещении на расстояние ​\( s \)​ равна:

При сжатии или растяжении пружины сила ​\( F \)​ меняется линейно с расстоянием, поэтому работу этой силы по сжатию или растяжению пружины на расстояние \( s \) можно представить как произведение средней силы ​\( \overline{F} \)​ на перемещение \( s \):

Средняя \( \overline{F} \) сила определяется как:

где ​\( F_1=-kx_1 \)​ — это сила упругости в точке с координатой ​\( x_1 \)​, a \( F_2=-kx_2 \) — сила упругости в точке с координатой \( x_2 \)​. При этом перемещение ​\( s \)​ будет равно:

Подставляя выражения для \( s \) и \( \overline{F} \) в формулу работы, получим:

Члены ​\( \frac{kx^2_1}{2} \)​ и \( \frac{kx^2_2}{2} \) выражают упругую потенциальную энергию пружины ​\( E_{у1} \)​ и \( E_{у2} \) в точках с координатами ​\( x_1 \)​ и \( x_2 \), соответственно. Таким образом, работа силы упругости равна изменению упругой потенциальной энергии пружины:

Рассмотрим простой пример. Насколько возрастет упругая потенциальная энергия пружины с коэффициентом упругости 1,0·10-2 Н/м при сжатии ее на 10 см? Подставляя значения в формулу

получим:

Формула жесткости соединений пружин

Не стоит забывать о том, что в некоторых случаях проводится соединение тела нескольким пружинами. Подобные системы получили весьма широкое распространение. Определить жесткость в этом случае намного сложнее. Среди особенностей соединения можно отметить нижеприведенные моменты:

1. Параллельное соединение характеризуется тем, что детали размещаются последовательно. Подобный метод позволяет существенно повысить упругость создаваемой системы.
2. Последовательный метод характеризуется тем, что деталь подключаются друг к другу. Подобный способ подсоединения существенно снижает степень упругости, однако позволяет существенно увеличить максимальное удлинение. В некоторых случаях требуется именно максимальное удлинение.

В обеих случаях применяется определенная формула, которая определяет особенности подключения. Модуль силы упругости может существенно отличаться в зависимости от особенностей конкретного изделия.

При последовательном соединении изделий показатель рассчитывается следующим образом: 1/k=1/k₁+1/k₂+…+1/k_n. Рассматриваемый показатель считается довольно важным свойством, в данном случае он снижается. Параллельный метод подключения рассчитывается следующим образом: k=k₁+k₂+…k_n.

Подобные формулы могут использоваться при самых различных расчетах, чаще всего на момент решения математических задач.

Расчет жесткости цилиндрической пружины

Довольно просто понять как работает плоская пружина. Если положить на край письменного стола линейку и прижать один ее конец рукой к поверхности, но второй можно упруго изгибать, запасая и высвобождая энергию. Очевидно, что в момент изгиба расстояния между молекулами материала в некоторых фрагментах линейки увеличиваются, в некоторых уменьшаются. Электромагнитные связи, действующие между молекулами, стремятся вернуть вещество к прежнему геометрическому состоянию.

Несколько сложнее дело обстоит с цилиндрической пружиной. В ней энергия запасается не благодаря деформации изгиба, а за счет скручивания проволоки, из которой пружина навита, относительно продольной оси этой проволоки.

Представим сильно увеличенное сечение проволоки, из которой навита цилиндрическая пружина, выполненное перпендикулярной ее оси плоскостью. При таком рассмотрении можно абстрагироваться от спиральной формы и мысленно разбить весь объем проволоки на множество соприкасающихся торцевыми поверхностями “цилиндров”, диаметр которых равен диаметру проволоки, а высота стремится к нулю. Между соприкасающимися торцами действуют молекулярные силы, препятствующие деформации.

При растяжении или сжатии пружины угол наклона между витками изменяется. Соседние “цилиндры” при этом вращаются друг относительно друга в противоположных направлениях вокруг общей оси. В каждом таком сечении запасается энергия. Отсюда следует, что чем из более длинного куска проволоки навита пружина (здесь играют роль диаметр и высота цилиндра, а также шаг витка), тем большее количество энергии она способна запасти. Увеличение диаметра проволоки также повышает ее энергоемкость. В целом формула, учитывающая основные факторы жесткости пружины, выглядит так:

$k = \frac{r^4}{4R^3} \cdot \frac{G}{n}$,

• $R$ – радиус цилиндра пружины,
• $n$ – количество витков проволоки радиуса $r$,
• $G$ – коэффициент, зависящий от материала.

Подставим в формулу числовые значения, попутно переведя их в единицы системы СИ:

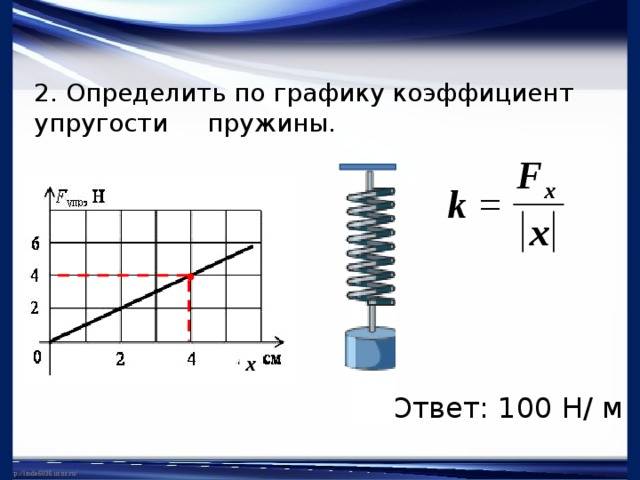
$k = \frac{(10^{-3})^4}{4 \cdot (2 \cdot 10^{-2})^3} \cdot \frac{8 \cdot 10^{10}}{25} = \frac{8 \cdot 10^{-2}}{10^2 \cdot 2^3 \cdot 10^{-6}} = 100$

Ответ: $100 \frac{Н}{м}$

При воздействии внешних сил тела способны приобретать ускорения или деформироваться. Деформацией называют изменение размеров и (или) формы тела. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.

Пусть на пружину на рис.1 действует растягивающая сила, направленная вертикально вниз.

При воздействии деформирующей силы ($\overline{F}$) длина пружины увеличивается. В пружине возникает сила упругости (${\overline{F}}_u$), которая уравновешивает деформирующую силу. Если деформация небольшая и упругая, то удлинение пружины ($\Delta l$) пропорционально деформирующей силе:

где в качестве коэффициента пропорциональности выступает жесткость пружины $k$. Коэффициент $k$ называют также коэффициентом упругости, коэффициентом жесткости. Жесткость (как свойство) характеризует упругие свойства тела, подвергаемого деформации – это возможность тела оказывать противодействие внешней силе, сохранять свои геометрические параметры. Коэффициент жесткости является основной характеристикой жесткости.

Коэффициент жесткости пружины зависит от материала, из которого изготовлена пружина, ее геометрических характеристик. Так, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси вычисляется при помощи формулы:

где $G$ -модуль сдвига (величина зависящая от материала); $d$ – диаметр проволоки; $d_p$ – диаметр витка пружины; $n$ – количество витков пружины.

Как использовать пружины соответственно их классу

Оба класса – «А» и «В», имеют абсолютно рабочие характеристики, и могут устанавливаться на автомобиль в равной степени. Единственное, что следует помнить при установке – цвета пружин подвески должны быть идентичны по обе стороны автомобиля. В противном случае может образоваться небольшой, но постоянный крен кузова на одну из сторон, что существенно ухудшит управляемость автомобилем и его устойчивость на дороге. Кроме того, если цвет пружин по жесткости будет отличаться, это приведет к ускоренному износу узлов всей «ходовки».

Специалисты достаточно часто говорят о необходимости использования на одном ТС элементов только одного класса. В крайнем случае, допускается устанавливать на переднюю ось пружины класса «А», на заднюю «В». Но ни в коем случае не наоборот – это категорически недопустимо. Чтобы избежать путаницы при самостоятельной замене, маркировка по цветам должна совпадать, так же как и их класс.

Важность пружинной константы

Чтобы полностью понять важность жесткости пружины с подразделами, включая «Значение в технике и физике» и «Использование жесткости пружины при проектировании механических систем». важно понимать соответствующую формулу и то, как она работает математически. . Используя уравнение закона Гука и формулу жесткости пружины, вы можете рассчитать жесткость пружины (k) пружин из определенного материала, что может помочь в определении силы, необходимой для сжатия, растяжения или деформации пружины. 

Используя уравнение закона Гука и формулу жесткости пружины, вы можете рассчитать жесткость пружины (k) пружин из определенного материала, что может помочь в определении силы, необходимой для сжатия, растяжения или деформации пружины. 

Эта линейная зависимость между силой и смещением имеет решающее значение в различных областях, таких как инженерия и физика.

Значение в технике и физике

Весна играет важную роль в технике и физике. Величина определяет, какая сила смещает пружину из равновесия. 

Помогает определить физические параметры, такие как масса, ускорение, энергия. Оптимизируйте проекты и эксперименты с помощью пружинных констант.

Измерьте изменение жесткости пружины в зависимости от напряжения или деформации. Отслеживайте изменения, чтобы указать на достижение предела. 

Обеспечивает оптимальное обслуживание и безопасность. Постоянная пружины – незамеченный герой механического дизайна.

Использование жесткости пружины при проектировании механических систем

Постоянная пружины имеет жизненно важное значение при проектировании механических систем. Это отношение силы к смещению и показывает, насколько жесткой или гибкой является пружина. . Давайте посмотрим на эту таблицу, чтобы получить представление о необходимой пружинной константе для каждого приложения:

Давайте посмотрим на эту таблицу, чтобы получить представление о необходимой пружинной константе для каждого приложения:

Заявление	Желаемая постоянная пружины (k)	Требуемый пружинный материал
Амортизатор	Низкий	Сталь
Часы	High	сплав
Генератор	Medium	Медь

Другие инновации

• Амортизаторы должны быть изготовлены из стали с низкой жесткостью пружины. Часы требуют высокой жесткости пружины, изготовленной из сплавов. 
• Для генераторов требуются средние пружинные константы, изготовленные из меди.
• Факторы окружающей среды также могут влиять на пружины. Изменения температуры и влажности могут привести к изменению размеров материалов, что повлияет на функциональность.
• Для оптимальной работы механических систем с пружинами инженеры должны выбирать материалы с соответствующими физическими свойствами и следить за условиями окружающей среды.

Формула определения жесткости

Изучаемая современными школьниками формула, как найти коэффициент жесткости пружины, представляет собой соотношение силы и величины, показывающей изменение длины пружины в зависимости от величины данного воздействия (или

Читать также: Бронза физические и химические свойства

равной ему по модулю силы упругости). Выглядит эта формула так: F = –kx. Из этой формулы коэффициент жесткости упругого элемента равен отношению силы упругости к изменению его длины. В международной системе единиц физических величин СИ он измеряется в ньютонах на метр (Н/м).

Другой вариант записи формулы: коэффициент Юнга

Деформация растяжения/сжатия в физике также может описываться несколько видоизмененным законом Гука. Формула включает значения относительной деформации (отношения изменения длины к ее начальному значению) и напряжения (отношения силы к площади поперечного сечения детали). Относительная деформация и напряжение по этой формуле пропорциональны, а коэффициент пропорциональности – величина, обратная модулю Юнга.

Модуль Юнга интересен тем, что определяется исключительно свойствами материала, и никак не зависит ни от формы детали, ни от ее размеров.

К примеру, модуль Юнга для ста

ли примерно равен единице с одиннадцатью нулями (единица измерения – Н/кв. м).

Смысл понятия коэффициент жесткости

Коэффициент жесткости – коэффициент пропорциональности из закона Гука. Еще он с полным правом называется коэффициентом упругости.

Фактически он показывает величину силы, которая должна быть приложена к упругому элементу, чтобы изменить его длину на единицу (в используемой системе измерений).

Значение этого параметра зависит от нескольких факторов, которыми характеризуется пружина:

• Материала, используемого при ее изготовлении.
• Формы и конструктивных особенностей.
• Геометрических размеров.

По этому показателю можно сд

елать вывод, насколько изделие устойчиво к воздействию нагрузок, то есть каким будет его сопротивление при приложении внешнего воздействия.

Особенности расчета пружин

Показывающая, как найти жесткость пружины, формула, наверное, одна из наиболее используемых современными конструкторами. Ведь применение эти упругие детали находят практически везде, то есть требуется просчитывать их поведение и выбирать те из них, которые будут идеально справляться с возложенными обязанностями.

Закон Гука весьма упрощенно показывает зависимость деформации упругой детали от прилагаемого усилия, инженерами используются более точные формулы расчета коэффициента жесткости, учитывающие все особенности происходящего процесса.

• Цилиндрическую витую пружину современная инженерия рассматривает как спираль из проволоки с круглым сечением, а ее деформация под воздействием существующих в системе сил представляется совокупностью элементарных сдвигов.
• При деформации изгиба в качестве деформации рассматривается прогиб стержня, расположенного концами на опорах.

Единицы измерения

При проводимых расчетах также должно учитываться то, в каких единицах измерениях проводятся вычисления

При рассмотрении того, чему равно удлинение пружины уделяется внимание единице измерения в Ньютонах

Для того чтобы упростить выбор детали многие производители указывают его цветовым обозначением.

Разделение пружины по цветам проводится в сфере автомобилестроения.

Среди особенностей подобной маркировки отметим следующее:

1. Класс А обозначается белым, желтым, оранжевым и коричневым оттенками.
2. Класса В представлен синим, голубым, черным и желтым цветом.

Как правило, подобное свойство отмечается на внешней стороне витка. Производители наносят небольшую полоску, которая и существенно упрощает процесс выбора.

Ход работы

II. Актуализация знаний.

• Что такое деформация?
• Сформулировать закон Гука
• Что такое жесткость и в каких единицах она измеряется.
• Дайте понятие об абсолютной и относительной погрешности.
• Причины, приводящие к появлению погрешностей.
• Погрешности, возникающие при измерениях.
• Как чертят графики результатов эксперимента.

Возможные ответы учащихся:

Деформация – изменение взаимного положения частиц тела, связанное с их перемещением относительно друг друга. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоков атомов. Деформации разделяют на обратимые (упругие) и необратимые (пластические, ползучести). Упругие деформации исчезают после окончания действия приложенных сил, а необратимые — остаются. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия; в основе пластических — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия.

Закон Гука: «Сила упругости, возникающая при деформации тела, пропорциональна его удлинению и направлена противоположно направлению перемещения частиц тела при деформации». Fупр = –kx

Жесткостью называют коэффициент пропорциональности между силой упругости и изменением длины пружины под действием приложенной к ней силы. Обозначают k. Единица измерения Н/м. Согласно третьему закону Ньютона, приложенная к пружине сила по модулю равна возникшей в ней силе упругости. Таким образом жесткость пружины можно выразить как: k = Fупр/x

Измерения никогда не могут быть выполнены абсолютно точно. Результат любого измерения приближенный и характеризуется погрешностью – отклонением измеренного значения физической величины от ее истинного значения. К причинам, приводящим к появлению погрешностей, относятся: – ограниченная точность изготовления средств измерения. – изменение внешних условий (изменение температуры, колебание напряжения) – действия экспериментатора (запаздывание с включением секундомера, различное положение глаза. ). – приближенный характер законов, используемых для нахождения измеряемых Величин

Погрешности, возникающие при измерениях, делятся на систематические и случайные. Систематические погрешности – это погрешности, соответствующие отклонению измеренного значения от истинного значения физической величины всегда в одну сторону (повышения или занижения). При повторных измерениях погрешность остается прежней. Причины возникновения систематических погрешностей: – несоответствие средств измерения эталону; – неправильная установка измерительных приборов (наклон, неуравновешенность); – несовпадение начальных показателей приборов с нулем и игнорирование поправок, которые в связи с этим возникают; – несоответствие измеряемого объекта с предположением о его свойствах.

Случайные погрешности – это погрешности, которые непредсказуемым образом меняют свое численное значение. Такие погрешности вызываются большим числом неконтролируемых причин, влияющих на процесс измерения (неровности на поверхности объекта, дуновение ветра, скачки напряжения и т.д.). Влияние случайных погрешностей может быть уменьшено при многократном повторении опыта.

Погрешности средств измерений. Эти погрешности называют еще инструментальными или приборными. Они обусловлены конструкцией измерительного прибора, точностью его изготовления и градуировки.

При построении графика по результатам опыта экспериментальные точки могут не оказаться на прямой, которая соответствует формуле F_упр = kx

Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы упругости и удлинения и вычислите жесткость k. Она и будет искомым средним значением жесткости пружины k_ср.

III. Порядок выполнения работы

1. Закрепите на штативе конец спиральной пружины (другой конец пружины снабжен стрелкой-указателем и крючком см. рис.).

2. Рядом с пружиной или за ней установите и закрепите линейку с миллиметровыми делениями.

3. Отметьте и запишите то деление линейки, против которого приходится стрелка-указатель пружины.

4. Подвесьте к пружине груз известной массы и измерьте вызванное им удлинение пружины.

5. К первому грузу добавьте второй, третий и т. д. грузы, записывая каждый раз удлинение |х| пружины.

По результатам измерений заполните таблицу:

Источник

Показатель жесткости цилиндрической пружины

В работе и в физике довольно огромную популярность получили собственно цилиндрические пружины. Их основными характерностями можно назвать такие моменты:

1. При разработке указывается главная ось, вдоль которой и действует большинство самых разных сил.
2. При изготовлении рассматриваемого изделия применяется проволока конкретного диаметра. Она делается из специализированного сплава или обыкновенных металлов. Необходимо помнить про то, что материал должен владеть очень высокой упругостью.
3. Проволока навинчивается виточками вдоль оси. При этом необходимо учесть, что они бывают одного или разнообразного диаметра. Довольно обширное распространение получил вариант выполнения цилиндрического типа, но большей стойкостью отличается цилиндрический вариант выполнения, в сжатом состоянии деталь обладает маленькой толщиной.
4. Важными параметрами можно назвать больший, малый и средний диаметр витков, диаметр проволки, шаг расположения некоторых колец.

Необходимо помнить про то, что выделяют два типа деталей: сжатия и растяжения. Их показатель жесткости устанавливается по одной и той же формуле. Разница состоит в следующем:

1. Вариант выполнения, рассчитан на сжатие, отличается дальним расположением витков. За счёт расстояние между ними имеется возможность сжатия.
2. Модель, которая рассчитана на растяжение, имеет кольца, размещенные фактически близко. Аналогичная форма определяет то, что при самая большая сила упругости достигается при минимальном растяжении.
3. Также имеется вариант выполнения, который рассчитывается на кручение и изгиб. Аналогичная деталь рассчитывается по конкретным формулам.

Расчет коэффициента цилиндрической пружины может проходит во время использования ранееуказанной формулы. Она определяет то, что критерий зависит от следующих показателей:

1. Наружного радиуса колец. Как раньше было отмечено, во время изготовления детали применяется ось, вокруг которой проходит накручивание колец. При этом необходимо помнить про то, что выделяют также усредненный и диаметр внутри. Аналогичный критерий указывается в техдокументации и на чертежах.
2. Количества создаваемых витков. Такой параметр в большинстве случаев определяет длину изделия в свободном состоянии. По мимо этого, кол-во колец определяет показатель жесткость и остальные параметры.
3. Радиуса используемой проволки. Для исходного материала применяется собственно проволока, которая делается из разных сплавов. В большинстве случаев ее свойства влияют на качества рассматриваемого изделия.
4. Модуля сдвига, который зависит от типа используемого материала.

Показатель жесткости является одним из наиболее основных параметров, который принимается во внимание при проведении довольно различных расчетов

Расчет жесткости системы

Встречаются более сложные задачи, в которых необходим расчет общей жесткости. В таких заданиях пружины соединены последовательно или параллельно.

Последовательное соединение системы пружин

При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:

1/k = 1/k1 + 1/k2 + … + 1/ki,

где k — общая жесткость системы, k1, k2, …, ki — отдельные жесткости каждого элемента, i — общее количество всех пружин, задействованных в системе.

Параллельное соединение системы пружин

В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:

k = k1 + k2 + … + ki.

Измерение жесткости пружины опытным путем — в этом видео.

Видео

Из этого видео вы узнаете, как определить жесткость пружины.

Чем большей деформации подвергается тело, тем значительней в нем возникает сила упругости. Это значит, что деформация и сила упругости взаимосвязаны, и по изменению одной величины можно судить об изменении другой. Так, зная деформацию тела, можно вычислить возникающую в нем силу упругости. Или, зная силу упругости, определить степень деформации тела.

Если к пружине подвешивать разное количество гирек одинаковой массы, то чем больше их будет подвешено, тем сильнее пружина растянется, то есть деформируется. Чем больше растянута пружина, тем большая в ней возникает силы упругости. Причем опыт показывает, что каждая следующая подвешенная гирька увеличивает длину пружины на одну и туже величину.

Так, например, если исходная длина пружины была 5 см, а подвешивание на ней одной гирьки увеличило ее на 1 см (т. е. пружина стала длиной 6 см), то подвешивание двух гирек увеличит ее на 2 см (общая длина составит 7 см), а трех — на 3 см (длина пружины будет 8 см).

Еще до опыта известно, что вес и возникающая под его действием сила упругости находятся друг с другом в прямопропорциональной зависимости. Кратное увеличение веса во столько же раз увеличит силу упругости. Опыт же показывает, что деформация точно также зависит от веса: кратное увеличение веса во столько же раз увеличивает изменения в длине. Это значит, что, исключив вес, можно установить прямопропорциональную зависимость между силой упругости и деформацией.

Если обозначить удлинение пружины в результате ее растяжения как x или как ∆ l ( l ₁ – l , где l — начальная длина, l ₁ — длина растянутой пружины), то зависимость силы упругости от растяжения можно выразить такой формулой:

В формуле используется коэффициент k . Он показывает, в какой именно зависимости находятся сила упругости и удлинение. Ведь удлинение на каждый сантиметр может увеличивать силу упругости одной пружины на 0,5 Н, второй на 1 Н, а третьей на 2 Н. Для первой пружины формула будет выглядеть как F_упр = 0,5x, для второй — F_упр = x, для третьей — F_упр = 2x.

Коэффициент k называют жесткостью пружины. Чем жестче пружина, тем труднее ее растянуть, и тем большее значение будет иметь k. А чем больше k, тем больше будет сила упругости (F_упр) при равных удлинения (x) разных пружин.

Жесткость зависит от материала, из которого изготовлена пружина, ее формы и размеров.

Единицей измерения жесткости является Н/м (ньютон на метр). Жесткость показывает, сколько ньютонов (сколько сил) надо приложить к пружине, чтобы растянуть ее на 1 м. Или насколько метров растянется пружина, если приложить для ее растяжения силу в 1 Н. Например, к пружине приложили силу в 1 Н, и она растянулась на 1 см (0,01 м). Это значит, что ее жесткость равна 1 Н / 0,01 м = 100 Н/м.

Также, если обратить внимание на единицы измерения, то станет понятно, почему жесткость измеряется в Н/м. Сила упругости, как и любая сила, измеряется в ньютонах, а расстояние – в метрах. Чтобы уровнять по единицам измерения левую и правую части уравнения Fупр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них)

Чтобы уровнять по единицам измерения левую и правую части уравнения Fупр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них)

Чтобы уровнять по единицам измерения левую и правую части уравнения Fупр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них).

Соотношение между силой упругости и деформацией упругого тела, описываемое формулой F_упр = kx, открыл английский ученый Роберт Гук в 1660 году, поэтому это соотношение носит его имя и называется законом Гука.

Упругой деформацией является такая, когда после прекращения действия сил, тело возвращается в свое исходное состояние. Бывают тела, которые почти нельзя подвергнуть упругой деформации, а у других она может быть достаточно большой. Например, поставив тяжелый предмет на кусок мягкой глины, вы измените его форму, и этот кусок сам уже не вернется в исходное состояние. Однако если вы растяните резиновый жгут, то после того, как отпустите его, он вернет свои исходные размеры. Следует помнить, что закон Гука применим только для упругих деформаций.

Формула F_упр = kx дает возможность по известным двум величинам вычислять третью. Так, зная приложенную силу и удлинение, можно узнать жесткость тела. Зная, жесткость и удлинение, найти силу упругости. А зная силу упругости и жесткость, вычислить изменение длины.

Заключение.

Значение модуля сдвига (G ) материала проволоки в существенной мере влияющее на жесткость пружины (C) в реальности колеблется от номинально принятого до ±10%. Это обстоятельство и определяет в первую очередь наряду с геометрической точностью изготовления пружины «правильность» расчетов усилий и соответствующих им перемещений.

Почему в расчетах не используются механические характеристики (допускаемые напряжения) материала проволоки кроме модуля упругости? Дело в том, что, задаваясь углом подъема витка и индексом пружины в ограниченных диапазонах значений, и придерживаясь правила: «угол подъема в градусах близок значению индекса пружины», мы фактически исключаем возможность возникновения касательных напряжений при эксплуатации превышающих критические величины. Поэтому проверочный расчет пружин на прочность имеет смысл производить лишь при разработке пружин для серийного производства в особо ответственных узлах. Но при таких условиях кроме расчетов всегда неизбежны серьезные испытания…

ПрошуУВАЖАЮЩИХтруд автора скачать файлПОСЛЕ ПОДПИСКИна анонсы статей.

ОСТАЛЬНЫМ можно скачать просто так… – никаких паролей нет!

Определение

Силу, которая возникает в результате деформации тела и пытающаяся вернуть его в исходное состояние, называют силой упругости.

Чаще всего ее обозначают ${\overline{F}}_{upr}$. Сила упругости появляется только при деформации тела и исчезает, если пропадает деформация. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.

Современник И. Ньютона Р. Гук установил зависимость силы упругости от величины деформации. Гук долго сомневался в справедливости своих выводов. В одной из своих книг он привел зашифрованную формулировку своего закона. Которая означала: «Ut tensio, sic vis» в переводе с латыни: каково растяжение, такова сила.

Рассмотрим пружину, на которую действует растягивающая сила ($\overline{F}$), которая направлена вертикально вниз (рис.1).

Силу $\overline{F\ }$ назовем деформирующей силой. От воздействия деформирующей силы длина пружины увеличивается. В результате в пружине появляется сила упругости (${\overline{F}}_u$), уравновешивающая силу $\overline{F\ }$. Если деформация является небольшой и упругой, то удлинение пружины ($\Delta l$) прямо пропорционально деформирующей силе:

где в коэффициент пропорциональности называется жесткостью пружины (коэффициентом упругости) $k$.

Жесткость (как свойство) – это характеристика упругих свойств тела, которое деформируют. Жесткость считают возможностью тела оказать противодействие внешней силе, способность сохранять свои геометрические параметры. Чем больше жесткость пружины, тем меньше она изменяет свою длину под воздействием заданной силы. Коэффициент жесткости – это основная характеристика жесткости (как свойства тела).

Коэффициент жесткости пружины зависит от материала, из которого сделана пружина и ее геометрических характеристик. Например, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси может быть вычислена как:

где $G$ – модуль сдвига (величина, зависящая от материала); $d$ – диаметр проволоки; $d_p$ – диаметр витка пружины; $n$ – количество витков пружины.

Единицей измерения коэффициента жесткости в Международной системе единиц (Си) является ньютон, деленный на метр:

\=\frac{\left}{\left}=\frac{Н}{м}.\]

Коэффициент жесткости равен величине силы, которую следует приложить к пружине для изменения ее длины на единицу расстояния.