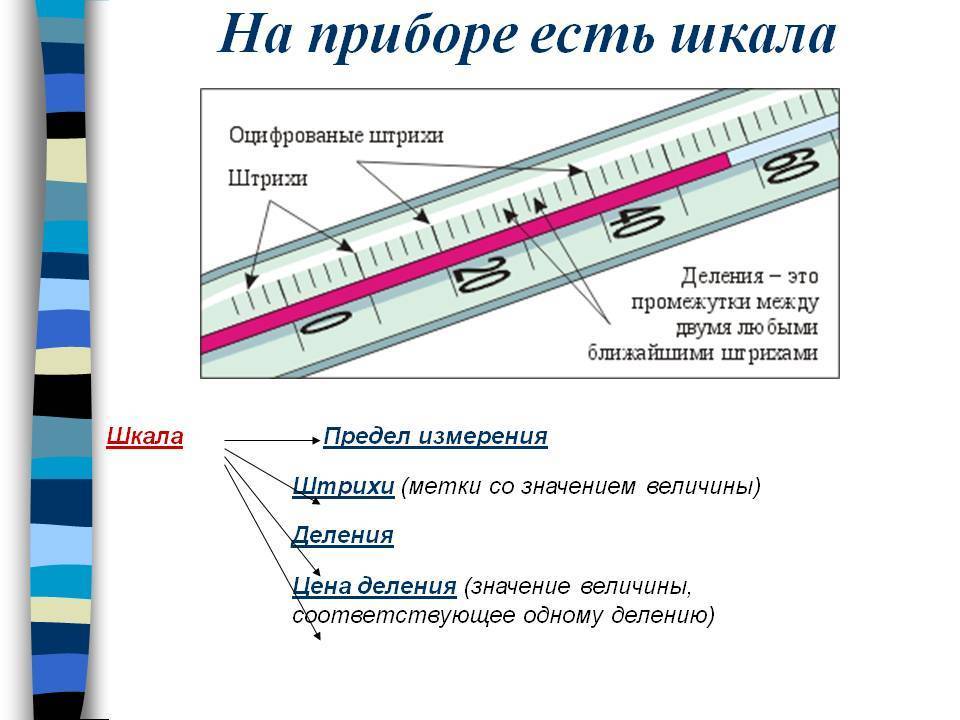
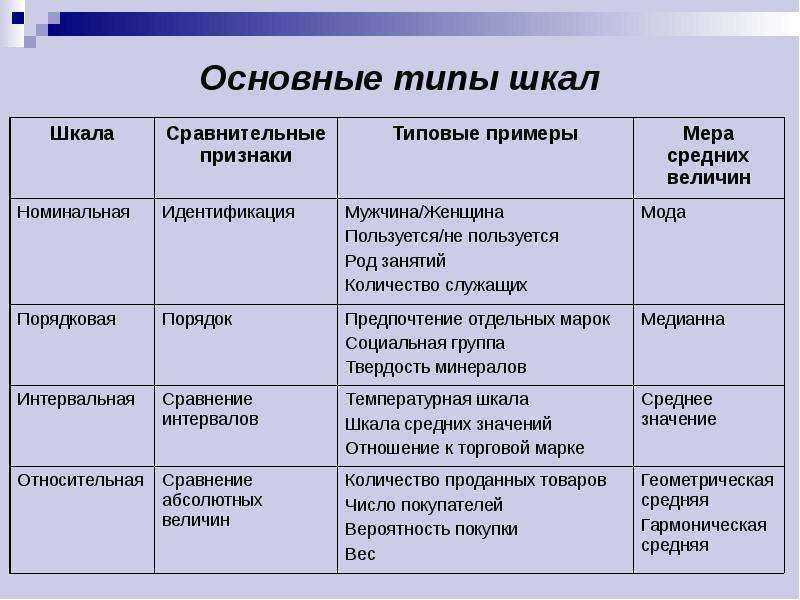
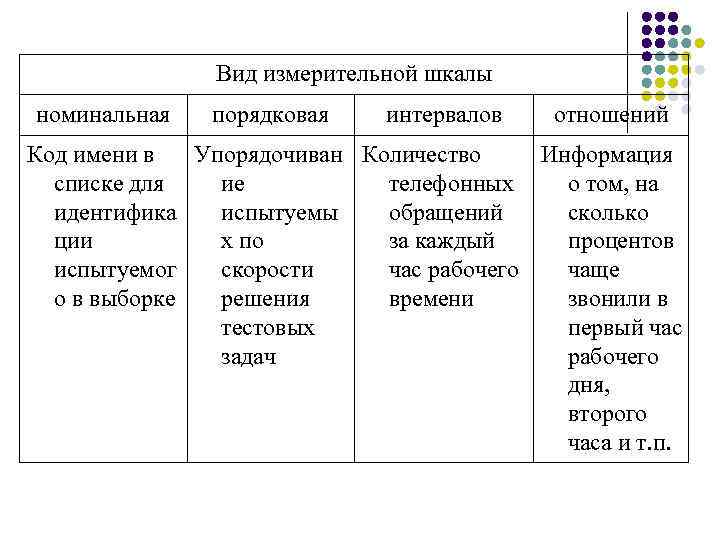
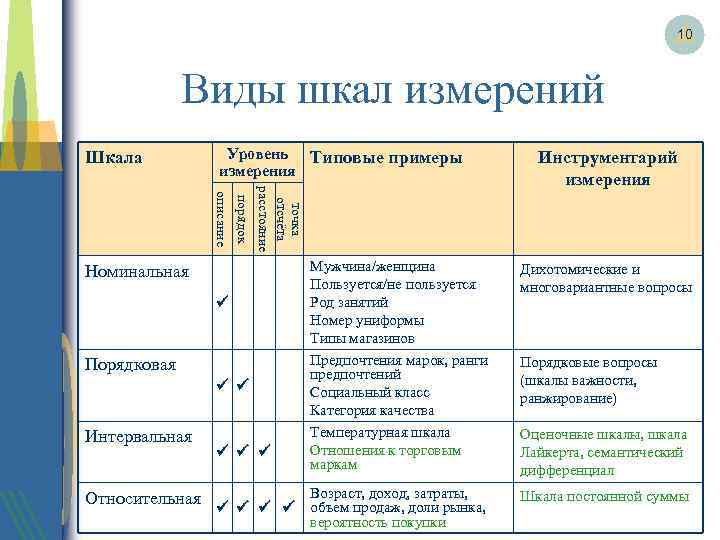
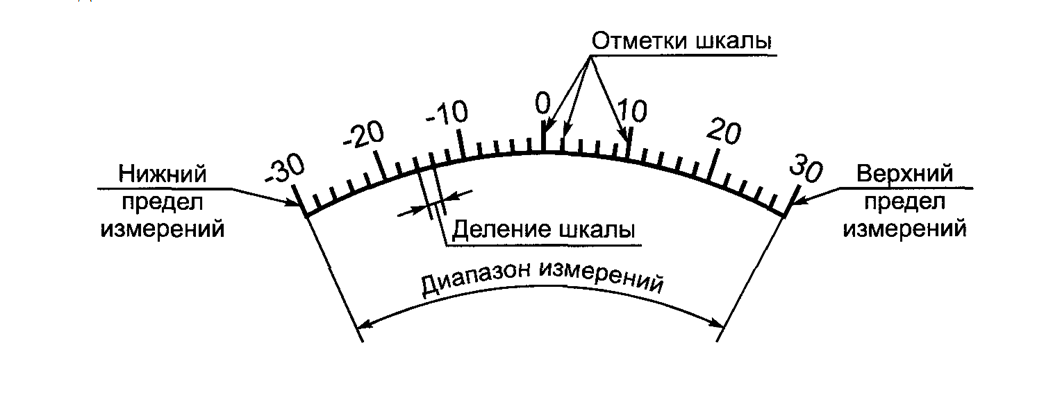
Принцип измерения горизонтального угла
Поверка
Меры длины
Величинами называют все, что поддается измерению. Так говорят о длине, площади, объеме, массе, времени, скорости. Величины — результат измерений, число, выраженное в определенных единицах. Последние известны как единица измерения.
Чтобы обозначить величину, пишут число, а рядом с ним указывают единицу, в которой проводилось измерение. К примеру, 3 см, 15 кг, 20 км, 2 мин. Для каждой величины общее число возможных значений не ограничено. Так, длина может быть 1 см, 10 см, 100 см и т. д. Одну и ту же величину в разных единицах выражают с помощью разных чисел.
Угловатый почерк: анализ, о чем он говорит
Кроме того, одну и ту же величину могут выражать по-разному. Например, используются различные единицы измерения длины в зависимости от того, насколько она маленькая или большая. В школе используются такие из них:
- Наименьшая единица — миллиметр (мм). Его легко увидеть на самой обычной линейке, которая есть у каждого школьника. Это самое маленькое деление, а точнее расстояние между ними.
- Следующей единицей стал сантиметр (см). На линейках сантиметры обозначаются числами. Один сантиметр состоит из десяти миллиметров. Между этими величинами ставится знак равенства, так как с их помощью обозначается одна и та же длина: 1 см = 10 мм.
- За сантиметром следует дециметр (дм). Один дециметр состоит из десяти сантиметров. Эти величины также равны, что обозначается следующим уравнением: 1 дм = 10 см.
- За дециметром следует метр (м), который содержит десять дециметров, то есть 1 м = 10 дм. В домашних условиях метр проще всего увидеть, если взять рулетку, длина которой часто составляет 1 метр. Сколько сантиметров в нем и как переводят сантиметры в метры? Один метр содержит десять дециметров, а они, в свою очередь, сто сантиметров (1 м = 10 дм = 100 см).
- Самая большая единица в этой категории в рамках стандартной школьной программы — километр. Один километр состоит из тысячи метров, что обозначается так: 1 км = 1000 м. Километры используются для измерений расстояний между странами и городами. Можно, конечно, переводить миллиметры в метры и далее, но более крупные величины все же удобнее.
Китайский календарь беременности: 2021 год
Существуют и более крупные меры, например мегаметры, гигаметры, тераметры, но они выходят за рамки знаний, необходимых школьнику.

Таким образом, меры величин, с помощью которых можно измерить длину, таковы:

Примечания
- Журавлев Ю.И., Рязанов В. В., Сенько О. В. «Распознавание». Математические методы. Программная система. Практические применения. — М.: Фазис, 2006. ISBN 5-7036-0108-8.
- ↑ Анфилатов В. С., Емельянов А. А., Кукушкин А. А. Системный анализ в управлении. — М. Финансы и статистика, 2002. — 368 с.
- Перегудов Ф. И., Тарасевич Ф. П. Введение в системный анализ. — М.: Высшая школа, 1989. — 367 с.
- ↑ Бахрушин В.Є. Методи аналізу даних. — Запоріжжя, КПУ, 2011
- ↑
- Mosteller, Frederick. Data analysis and regression : a second course in statistics (англ.). — Reading, Mass: Addison-Wesley Pub. Co, 1977. — ISBN 978-0201048544.
- Wolman, Abel G. Measurement and meaningfulness in conservation science (англ.) // Conservation biology : journal. — 2006.
- . Institute for Digital Research and Education. University of California, Los Angeles. Дата обращения: 7 февраля 2016.
- Суппес П., Зиннес Д. Основы теории измерений // Психологические измерения. М.: 1967. С. 9-110.
Общие сведения об измерениях. Погрешности измерений и средств измерений
Общие сведения об измерениях
Измерение – нахождение значения физической величины опытным путем с помощью специальных технических средств. Под измерением понимается процесс экспериментального сравнения данной физической величины с однородной физической величиной, значение которой принято за единицу.
Мера – средство измерений, предназначенное для воспроизведения физической величины заданного размера.
Измерительный прибор – средство измерений, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем. Измерительные приборы классифицируются по различным признакам. Например, измерительные приборы можно построить на основе аналоговой схемотехники или цифровой. Соответственно их делят на аналоговые и цифровые. Ряд приборов, выпускаемых промышленностью, допускают только отсчитывание показаний. Эти приборы называются показывающими. Измерительные приборы, в которых предусмотрена регистрация показаний, носят название регистрирующих.
Погрешности измерений
Погрешность является одной из основных характеристик средств измерений.
Под погрешностью электроизмерительных приборов, измерительных преобразователей и измерительных систем понимается отклонение их выходного сигнала от истинного значения входного сигнала.
Абсолютная погрешность Δa прибора есть разность между показанием прибора ах и истинным значением а измеряемой величины, т.е.
Абсолютная погрешность, взятая с обратным знаком, называется поправкой.
Относительная погрешность δ представляет собой отношение абсолютной погрешности к истинному значению измеряемой величины. Относительная погрешность, обычно выражаемая в процентах, равна
Приведенная погрешность γП есть выраженное в процентах отношение абсолютной погрешности Δa к нормирующему значению апр
Нормирующее значение – условно принятое значение, могущее быть равным конечному значению диапазона измерений (предельному значению шкалы прибора).
Погрешности средств измерений
Класс точности прибора указывают просто числом предпочтительного рода, например, 0,05. Это используют для измерительных приборов, у которых предел допускаемой приведенной погрешности постоянен на всех отметках рабочей части его шкалы (присутствует только аддитивная погрешность). Таким способом обозначают классы точности вольтметров, амперметров, ваттметров и большинства других однопредельных и многопредельных приборов с равномерной шкалой.
Класс точности прибора (например, амперметра) дается выражением
При установлении классов точности приборов нормируется приведенная погрешность, а не относительная. Причина этого заключается в том, что относительная погрешность по мере уменьшения значений измеряемой величины увеличивается.
По ГОСТ 8.401-80 в качестве значений класса точности прибора используется отвлеченное положительное число из ряда:
В интервале от 1 до 100 можно использовать в качестве значений класса точности числа:
(α = 0) 1; 1,5; 2; 2,5; 4; 5; 6;
(α = 1) 10; 15; 20; 25; 40; 50; 60.
Т.е. четырнадцать чисел 1; 1,5; 2; 2,5; 4; 5; 6; 10; 15; 20; 25; 40; 50; 60.
Необходимо отметить, классы точности от 6,0 и выше считаются очень низкими.
Примеры решения задач
Задача №1
Определить для вольтметра с пределом измерения 30 В класса точности 0,5 относительную погрешность для точек 5, 10, 15, 20, 25 и 30 В и наибольшую абсолютную погрешность прибора.
Решение
- Класс точности указывают просто числом предпочтительного рода, например, 0,5. Это используют для измерительных приборов, у которых предел допускаемой приведенной погрешности постоянен на всех отметках рабочей части его шкалы (присутствует только аддитивная погрешность). Таким способом обозначают классы точности вольтметров, амперметров, ваттметров и большинства других однопредельных и многопредельных приборов с равномерной шкалой.
Приведенная погрешность (выраженное в процентах отношение абсолютной погрешности к нормирующему значению)
постоянна и равна классу точности прибора.
Относительная погрешность однократного измерения (выраженное в процентах отношение абсолютной погрешности к истинному значению измеряемой величины)
уменьшается к значению класса точности прибора с ростом измеренного значения к предельному значению шкалы прибора.
Абсолютная погрешность однократного измерения
постоянна на всех отметках рабочей части шкалы прибора.
По условию задачи: Uизм = Ui = 5, 10, 15, 20, 25 и 30 В – измеренное значение электрической величины; Uпр = 30 В – предел шкалы вольтметра.
Наибольшая абсолютная погрешность вольтметра
Источник
Классы точности болтов
Болты и другие крепежные изделия изготавливают нескольких классов:
Каждый из них имеет свои допуски измеряемой величины, отличные от остальных и применяется в различных сферах.
Крепеж С используют в отверстиях с диаметром немногим больше диаметра болта (до 3мм). Болты без труда устанавливаются, не отнимая много времени на работу. Из минусов стоит отметить то, что при физическом воздействии на такой крепеж, болтовое соединение может сместиться на несколько миллиметров.
Крепеж В подразумевает использование болтов, диаметр которых меньше отверстия в пределах 1-1,5 мм. Это позволяет конструкции меньше подвергаться смещениям и деформациям, но повышаются требования к изготовлению отверстий в креплениях.
Гайки шестигранные класса точности В
Крепеж А создается по проекту. Диаметр болта такого типа, меньше диаметра отверстия максимум на 0,3 мм и имеет допуск только со знаком минус. Это делает крепеж неподвижным, не позволяет происходить смещению узлов. Изготовление болтов А-класса стоит дороже и не всегда используется в производстве.
Класс точности присутствует в описании всех измерительных приборов и является одной из самых важных характеристик. Чем выше его значение, тем более дорогостоящий будет прибор, но в то же время он сможет предоставить более точную информацию. Выбор стоить делать исходя из сложившейся ситуации и целей в которых будет использоваться такое средство
Важно понимать, что в некоторых ситуациях экономически выгодно будет приобрести дорогостоящее сверхточное оборудование, чтобы в дальнейшем сберечь деньги
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
В соответствии с ГОСТ 8.401-80 все средства измерений делятся на классы точности, которые устанавливают в стандартах или технических условиях, содержащих технические требования к СИ, подразделяемым по точности. Классы точности СИ конкретного типа выбирают соответственно из ряда классов точности, регламентированных в стандартах или других НД на СИ рассматриваемого вида. В данных стандартах устанавливают конкретные требования к метрологическим характеристикам, отражающим уровень точности СИ этого класса.
Классы точности присваивают средствам измерений при их разработке с учетом результатов государственных приемочных испытаний. Как было указано выше, пределы основной и дополнительной погрешностей следует выражать в форме абсолютных, относительных или приведенных погрешностей в зависимости от характера измерения погрешностей в пределах диапазона измерений конкретного вида СИ.
Пределы допускаемой основной погрешности, выражаемые абсолютной систематической погрешностью, наиболее часто используются для характеристики погрешностей, возникающих по вине схем СИ. Однако их значение можно уменьшить за счет регулировки определенных элементов схем, вариации параметров влияния которых заметно сказывается на так называемых аддитивных и мультипликативных погрешностях.
Обозначение классов точности СИ в документации может осуществляться в форме абсолютных погрешностей или относительных погрешностей (таблица 4.1).
При этом классы точности следует обозначать в документации прописными буквами латинского алфавита или римскими цифрами. В необходимых случаях к обозначению класса точности буквами латинского алфавита допускается добавлять индексы в виде арабской цифры. Классам точности, которым соответствуют меньшие пределы допускаемых погрешностей, должны соответствовать буквы, находящиеся ближе к началу алфавита, или цифры, означающие меньшие числа.
В эксплуатационной документации на СИ конкретного вида, содержащей обозначение класса точности, должна быть ссылка на стандарт или технические условия, в которых установлен класс точности данного СИ.
Стандарт ГОСТ 8.401—80 предусматривает определенные обозначения классов точности на СИ. В соответствии с указанным стандартом условные обозначения классов точности наносятся на циферблаты, щитки и корпуса СИ. Они включают числа, прописные буквы латинского алфавита или римские цифры. За исключением технически обоснованных случаев, вместе с условным обозначением класса точности на циферблат, щиток или корпус СИ должны быть нанесены обозначения стандартов или ТУ, устанавливающих технические требования к этим СИ.
На СИ одного и того же класса точности, которые эксплуатируются в различных условиях, следует наносить обозначение условий их эксплуатации, предусмотренные в стандартах или ТУ на СИ.
Правила построения и примеры обозначения классов точности приведены в таблице 4.1.
Таблица 4.1. Формулы вычисления погрешностей и обозначение классов точности СИ
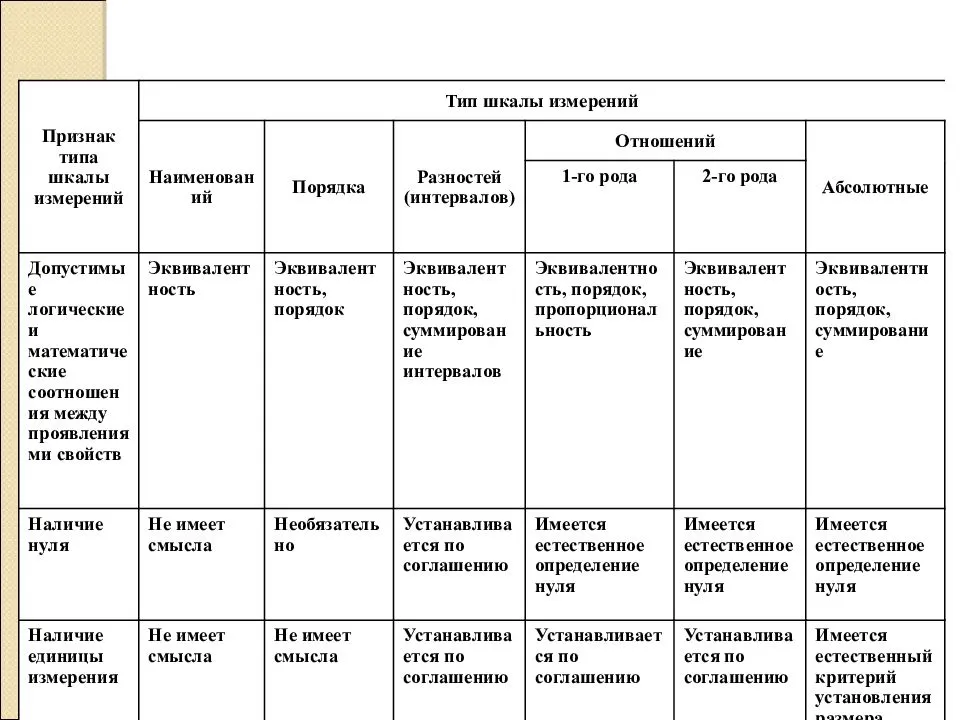
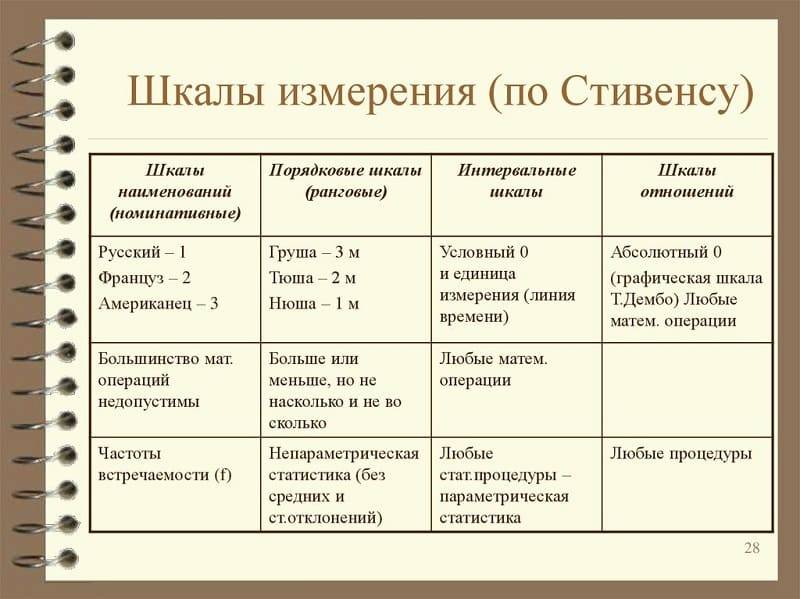
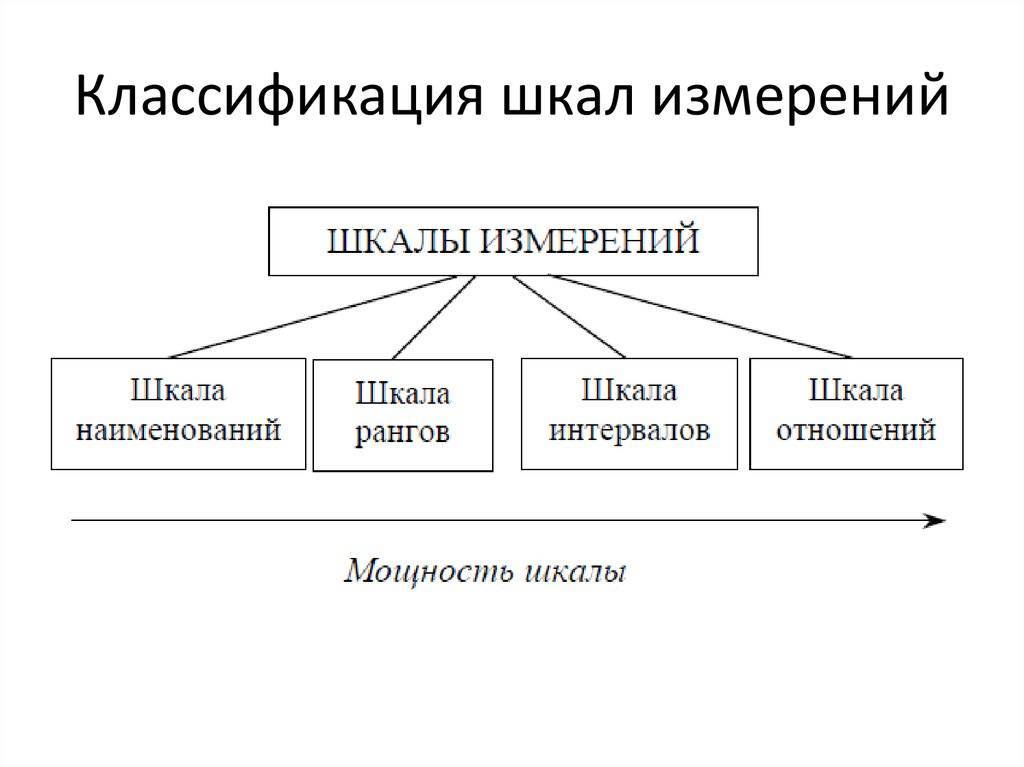
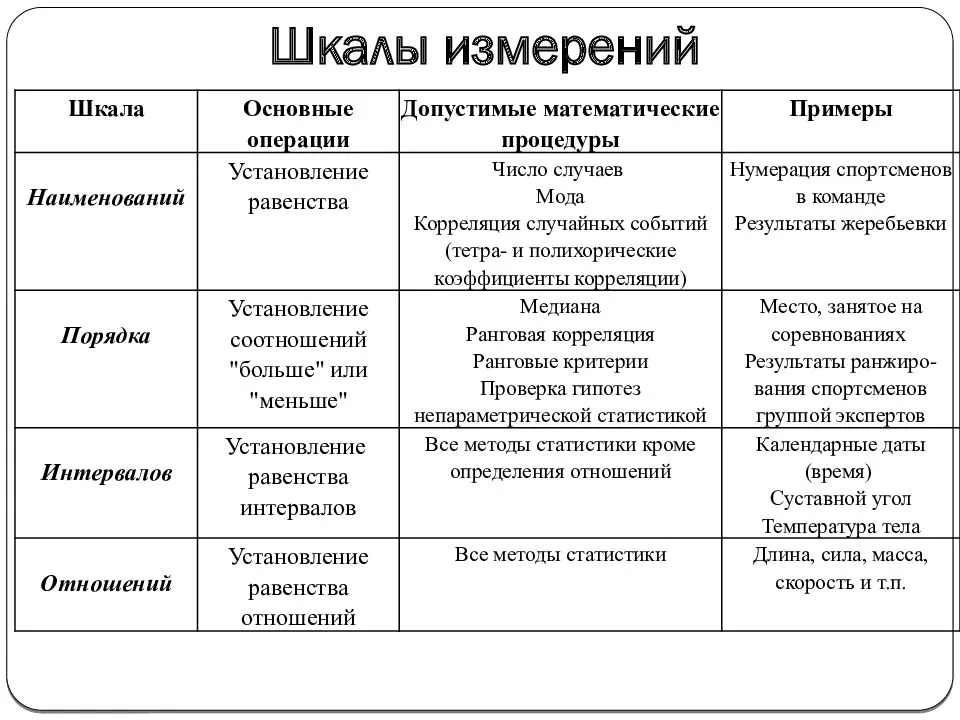
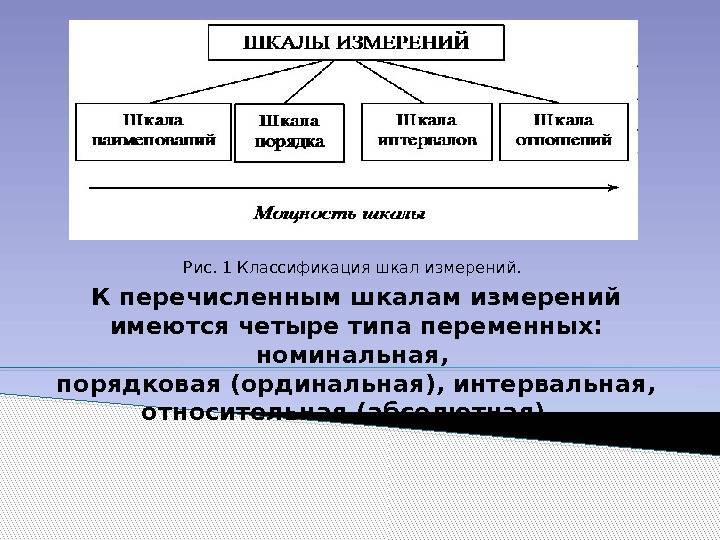
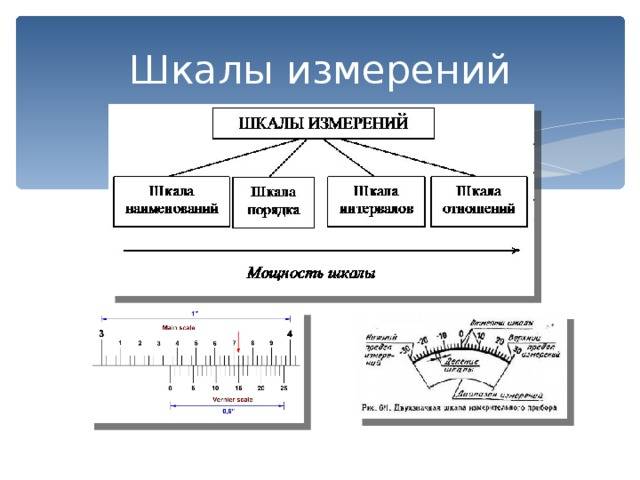
Шкала измерения
Определение 1
Шкала – это особый способ измерения социального объекта.
Измерение в социологии понимается в двух аспектах:
- теоретически, в рамках дискуссии о применимости математических методов в социологических исследованиях, их возможностях, границах, характере качественных и количественных методов;
- эмпирически, как построение шкал.
При изучении социальной реальности социолога, как правило, интересуют отношения, в которые входит объект исследования (например, как мы относимся к нашей профессии, к нашему учебному заведению, к тому или иному виду деятельности). Чтобы как-то исправить, «поймать» эти отношения, социолог соотносит их с любой числовой системой. Числовая система представляет собой шкалу
Шкала наименований
Данная шкала еще называется номинальной. Она является самой простой. Числа в ней играют роль ярлыков. Они нужны для того, чтобы обнаруживать и различать изучаемые объекты. Числа, которые составляют данную шкалу, разрешено менять местами. В ней нет никаких отношений типа «меньше-больше». По этой причине некоторые думают, что ее применение не стоит принимать за измерение. Используя шкалу наименований, можно проводить лишь небольшое число математических операций. К примеру, нельзя вычитать и складывать ее числа, но можно посчитать, сколько раз встречается определенное число.
Использование в психометрии
Основная статья: Психометрия
Используя различные шкалы, можно производить различные психологические измерения. Самые первые методы психологических измерений были разработаны в психофизике. Основной задачей психофизиков являлось то, каким образом определить, как соотносятся физические параметры стимуляции и соответствующие им субъективные оценки ощущений. Зная эту связь, можно понять, какое ощущение соответствует тому или иному признаку. Психофизическая функция устанавливает связь между числовым значением шкалы физического измерения стимула и числовым значением психологической или субъективной реакцией на этот стимул.
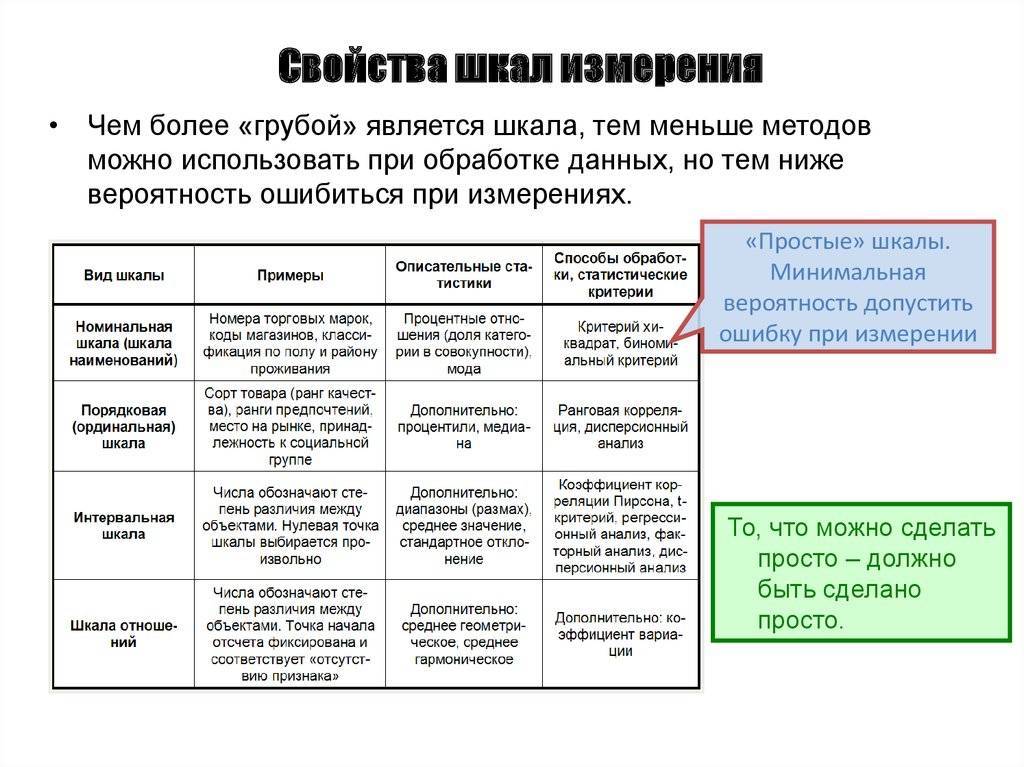
Номинальные шкалы
Номинальная шкала (nominal scale), или шкала наименований 1, сопоставляет каждый объект с определённым признаком. В результате объект либо обладает этим признаком, либо нет. Номинальная шкала состоит из названий — это самое простое и в то же время верное понимание номинальной шкалы. Пример. Красное или чёрное — это измерение в некой цветовой гамме. Многие классификации, ответы на вопросы анкеты — всё это примеры номинальных измерений. С них начинается работа создателей сбалансированной системы показателей, а закончиться она должна цифрами
Но здесь важно не переборщить и оставить номинальные измерения только там, где они предпочтительнее формальной оцифровки
Как правильно пользоваться шкалами, чтобы получить достоверные первичные измерения? Это не такой простой вопрос, как кажется на первый взгляд.
Допустимые преобразования. В номинальной шкале допустимыми преобразованиями (см. врезку) являются все взаимно-однозначные преобразования 2. Например, red — это «красный». Никаких отношений, кроме «равно» и «неравно», здесь нет. В этой шкале числа используются лишь как метки (как, например, при сдаче белья в прачечную), то есть лишь для различения объектов.
Допустимые преобразования
Этим понятием математики строго описывают шкалы. Тип шкалы задаётся группой её допустимых преобразований. Допустимые преобразования — это такие преобразования, которые не меняют соотношения между объектами измерения и, соответственно, выводы, сделанные по результатам измерений.Например, при измерении длины переход от аршинов к метрам не меняет соотношений между длинами рассматриваемых объектов: если первый объект длиннее второго в пять раз, то это будет установлено при измерении как в аршинах, так и в метрах
Обратите внимание, что при этом численное значение длины в аршинах отличается от длины в метрах — не меняется лишь результат сравнения длин двух объектов. Аналогично денежные суммы можно сопоставлять как в рублях, так и в иностранной валюте
Особенность, связанная с изменяющимися курсами валют: результат сопоставления денежных сумм в разных валютах меняется во времени. С аршинами и метрами ситуация иная: их соотношение вечно. Вот вам и проблема курсовых разниц в экономике. О ней сейчас не место говорить, но запомните её.
Интервальная шкала
Это такой тип, в котором числа не просто являются упорядоченными по рангам, но и разделяются определенными промежутками. Нулевая точка в данной шкале выбирается произвольно. Это отличает ее от шкалы отношений. В качестве примеров можно привести календарное время (в различных календарях начало исчисления лет устанавливалось по каким-то случайным причинам), потенциал электрополя, температуру, потенциальную энергию поднятого груза.
Результаты, получаемые путем измерения по этой шкале, можно обрабатывать любым математическим методом, кроме определения отношений. Данные, которые показывает шкала, отвечают на вопрос «на сколько меньше или больше?», но не дают возможности утвердительно говорить, что одно из значений исследуемой величины во сколько-то раз меньше или больше, чем другое. К примеру, если температура в помещении с 10 градусов повысилась до 20, нельзя сказать, что теперь в два раза теплее.
Уровень коэффициента
Шкала коэффициента в дополнение ко всем атрибутам, отражённым номинальным, порядковым и интервальным уровнями, отражает атрибут коэффициента. И снова вернёмся к результатам в таблице. Значения в колонке Z (показания секундомера Z) могут быть получены из показаний колонки U (секундомер U — истинное время) с помощью простой формулы:
Коэффициент измерений между Z и U остаётся одинаковым. Например, коэффициент соотношения (Sayyed/Shatakshi) в колонке Z (22/26) такой же, как и в колонке U (11/13). Глядя на колонку Z, можно уверенно заключить, что “Shweta бежал вдвое дольше, чем Surbhi”
Также обратите внимание, что точка отсчёта секундомера верна. Navjot не участвовал в забеге, поэтому в показаниях секундомеров U и Z мы видим 0. Отсюда следует, что шкала коэффициента имеет ‘абсолютный ноль’ (точку, где измеряемых качеств не существует)
Например, ‘ноль градусов’ на шкале Кельвина (находящейся на уровне коэффициента) означает полное отсутствие температуры
Отсюда следует, что шкала коэффициента имеет ‘абсолютный ноль’ (точку, где измеряемых качеств не существует). Например, ‘ноль градусов’ на шкале Кельвина (находящейся на уровне коэффициента) означает полное отсутствие температуры.
Большая часть научных и инженерных измерений выполняется на шкалах коэффициента. В науке измерение обычно определяется как вычисление коэффициента между значением непрерывной величины и величиной единицы измерения того же рода. Некоторые примеры измерений по шкале коэффициента: концентрация химического вещества, плотность потока фотосинтетических фотонов, температура в Кельвинах, масса, длина, время, угол на плоскости, энергия, давление и электрический заряд.
Определить по какой шкале производится измерение: интервальной или коэффициента можно, задав два вопроса: имеет ли здесь смысл ноль? Допустимы ли операторы удвоения или деления пополам?
Также важно отметить, что некоторые научные измерения не попадают ни в один из этих уровней. Их примеры включают шкалу pH и значения logIC50. Оба этих измерения проводятся по логарифмической шкале
Как бы то ни было, когда эти значения выражаются на шкале концентрации (H+ion концентрация для значений pH или IC50), измерения попадают в уровень коэффициента
Оба этих измерения проводятся по логарифмической шкале. Как бы то ни было, когда эти значения выражаются на шкале концентрации (H+ion концентрация для значений pH или IC50), измерения попадают в уровень коэффициента.
Порядковые шкалы
Порядковая шкала отражает более высокий уровень измерений, учитывающий, к какой категории принадлежит объект и в каком отношении он находится с другими объектами. В порядковой шкале числа используются не только для различения объектов, но и для установления порядка между ними.Пример. Простейшим примером порядковой шкалы служат оценки знаний учащихся. Символично, что в средней школе применяются оценки 2, 3, 4, 5, а в высшей школе тот же смысл выражается словесно — «неудовлетворительно», «удовлетворительно», «хорошо», «отлично». Этим подчёркивается «нечисловой» характер оценок знаний студентов.Фактически измерение по порядковой шкале представляет собой операцию упорядочения. Предполагаются сравнения «больше — меньше» или «лучше — хуже». Например, мнения экспертов часто выражаются в порядковой шкале, то есть эксперт может сказать (и обосновать), что один показатель качества продукции важнее, чем другой; первый технологический объект опаснее, чем второй, и т. д. Но он не в состоянии сказать, во сколько раз или насколько он более важен, или, соответственно, более опасен.Допустимые преобразования. Порядковая шкала допускает любое возрастающее преобразование, то есть такое, которое не меняет порядок шкалы.Типы порядковых шкал. Используют два типа порядковых шкал, которые различны с практической точки зрения:
- ранговая шкала, которая предполагает присвоение объектам рангов (ранжирование);
- балльная шкала, в которой применяются баллы.
Обдумывание измерений некоторых показателей следует начать с выбора между ранговым и балльным типами шкал.
Поверка и юстировка цилиндрического уровня при алидаде горизонтального круга
Шкала порядка

Места, которые величины занимают в такой шкале, называются рангами. Саму шкалу также называют ранговой либо неметрической. В ней все числа упорядочиваются по занимаемым местам. Интервалы между ними нельзя точно измерить. Данная шкала дает возможность не только установить равенство или неравенство между измеряемыми объектами, но и определить характер неравенства в виде логических суждений типа «больше и меньше», «хуже и лучше».
При помощи шкалы порядка можно измерять показатели, являющиеся качественными, но не имеющие строгих количественных мер. Широкое применение нашли такие шкалы в психологии и педагогике, а также социологии.
Виды маркирования
Классы точности полностью всех приборов для измерений подлежат маркировке на шкале данных самых приборов в виде числа. Применяются арабские цифры, которые обозначают процент нормированной неточности. Обозначение класса точности в круге, к примеру число 1,0, говорит про то, что ошибочность показаний стрелки аппарата будет равна 1%.
Если в обозначении применяется помимо цифры еще и галочка, то это означает, что длина шкалы используется в роли нормирующего значения.
Латинские буквы для определения используются если его можно определить пределами полной неточности.
Есть аппараты, на шкалах которых нет информации о классе точности. В данных случаях полную следует приравнивать к одной второй наименьшего деления.
Как мы говорили до недавнего времени, прибор для измерений, благодаря нормированию уже имеет случайную и систематические ошибки. Однако следует знать, что они зависят от метода измерения, условий и прочих моментов. Чтобы значение величины, подлежащей замеру, было на 99% точным, средство измерения должно иметь небольшую погрешность. Относительная должна быть приблизительно на треть или четверть меньше неточности измерений.
Базовый способ определения неточности
Во время установки класса точности первым делом нормированию подлежат пределы допустимой ключевой неточности, а пределы позволяемой добавочной неточности имеют кратное значение от ключевой. Их пределы выражают в форме полной, относительной и приведенной.
Приведенная погрешность средства измерения – это относительная, выраженная отношением предельно-допустимой полной неточности к нормирующему критерию. Безоговорочная может быть выражается в виде числа или двучлена.
Если класс точности СИ будет определяться через полную, то его обозначают римскими числами или буквами латиницы. Чем ближе буква будет к началу алфавита, тем меньше позволяемая безоговорочная погрешность подобного устройства.
Класс точности 2,5
Благодаря относительной неточности можно назначить класс точности двумя вариантами. В первом варианте на шкале будет показана арабская цифра в кружке, в другом варианте дробью, числитель и знаменатель которой сообщают диапазон погрешностей.
Главная погрешность может быть только в образцовых условиях лаборатории. В жизни приходится множить данные на ряд специализированных коэффициентов.
Добавочная бывает в результате изменений величин, которые каким-нибудь образом оказывают влияние на измерения (к примеру температура или влажность). Выход за установленные пределы можно обнаружить, если сложить все дополнительные неточности.
Случайные ошибки имеют непредсказуемые значения В результате того, что факторы, оказывающие на них воздействие регулярно меняются во времени. Для их учета пользуются теорией допустимости из высшей математики и ведут записи происходивших до недавнего времени случаев.
Пример расчета неточности
Статистическая измерительного средства принимается во внимание при измерении какой-нибудь константы либо же нечасто подверженной изменениям величины. Динамическая принимается во внимание при замерах величин, которые часто меняют собственные значения за незначительный период времени
Динамическая принимается во внимание при замерах величин, которые часто меняют собственные значения за незначительный период времени
Статистические шкалы
Введение
Грамотное применение статистических методов обработки данных во многом зависит от четкого понимания исследователем того, в какой статистической шкале они представлены. Непонимание этого может привести к тому, что исследователь получит результаты, которые не отражают действительное положение вещей и сделает неправильные выводы. Именно поэтому понимание того, в какой шкале представлены статистические данные является одним из необходимых условий успешной и грамотной статистической обработки.
Итак, приступим к тому, чтобы разобраться, что же такое статистические шкалы.
Определения и примеры
Шкала (от лат. «скале» — лестница) – элемент счетной системы, посредством которого происходит отнесение исследуемого объекта к определенной группе объектов.
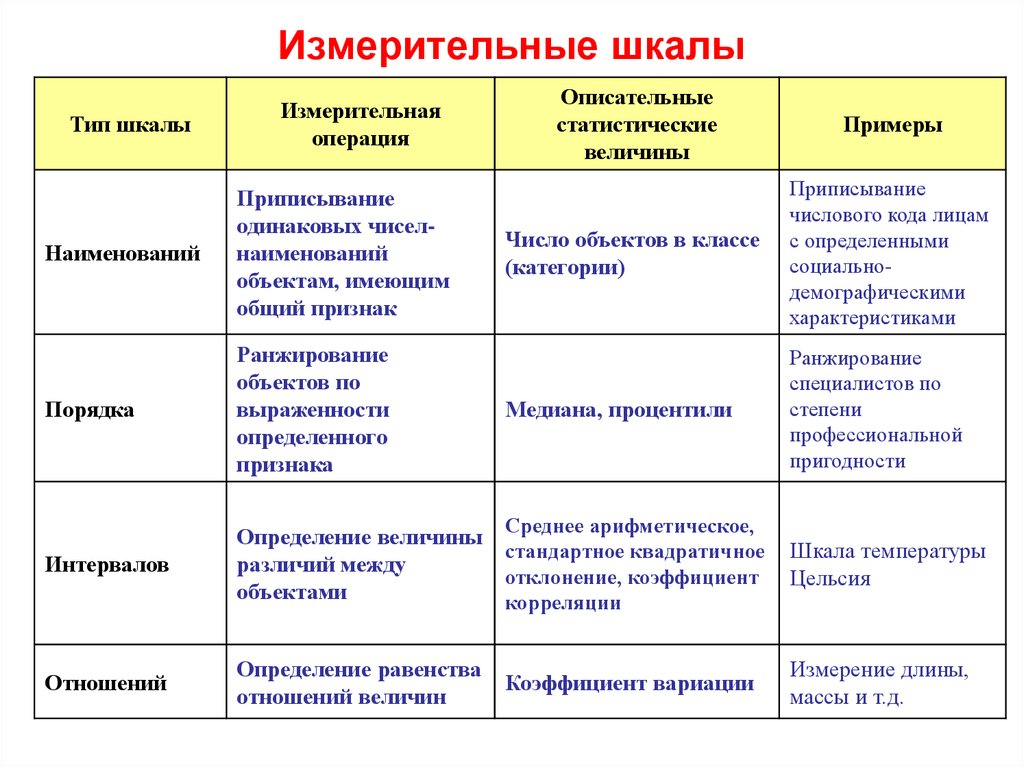
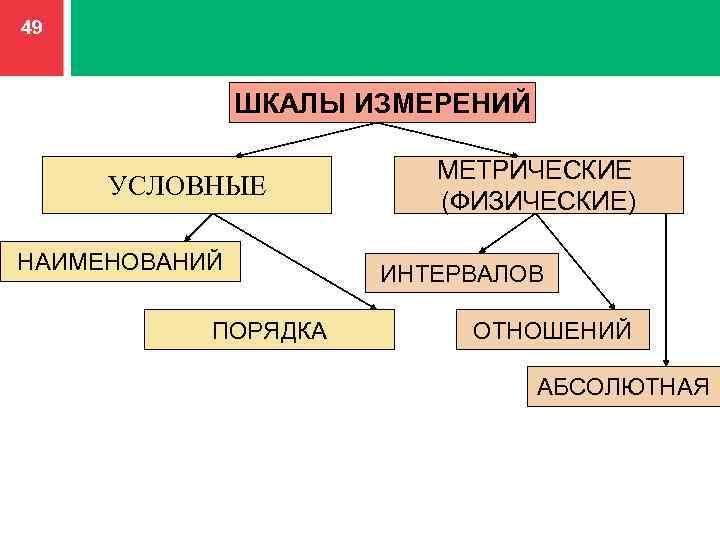
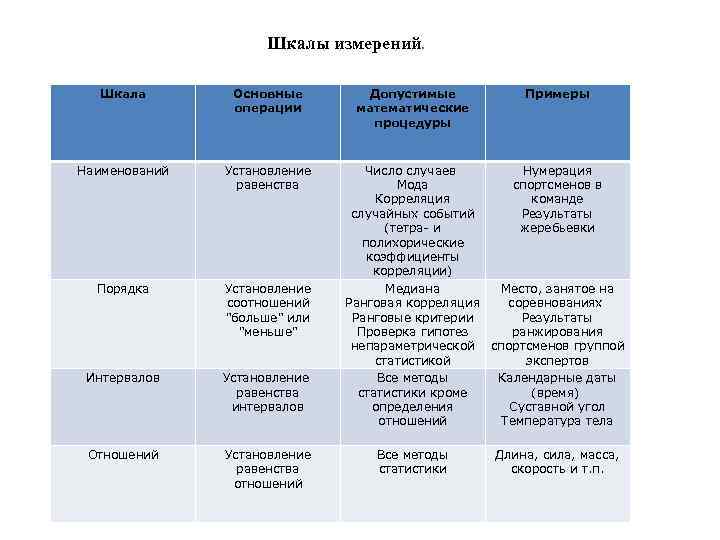
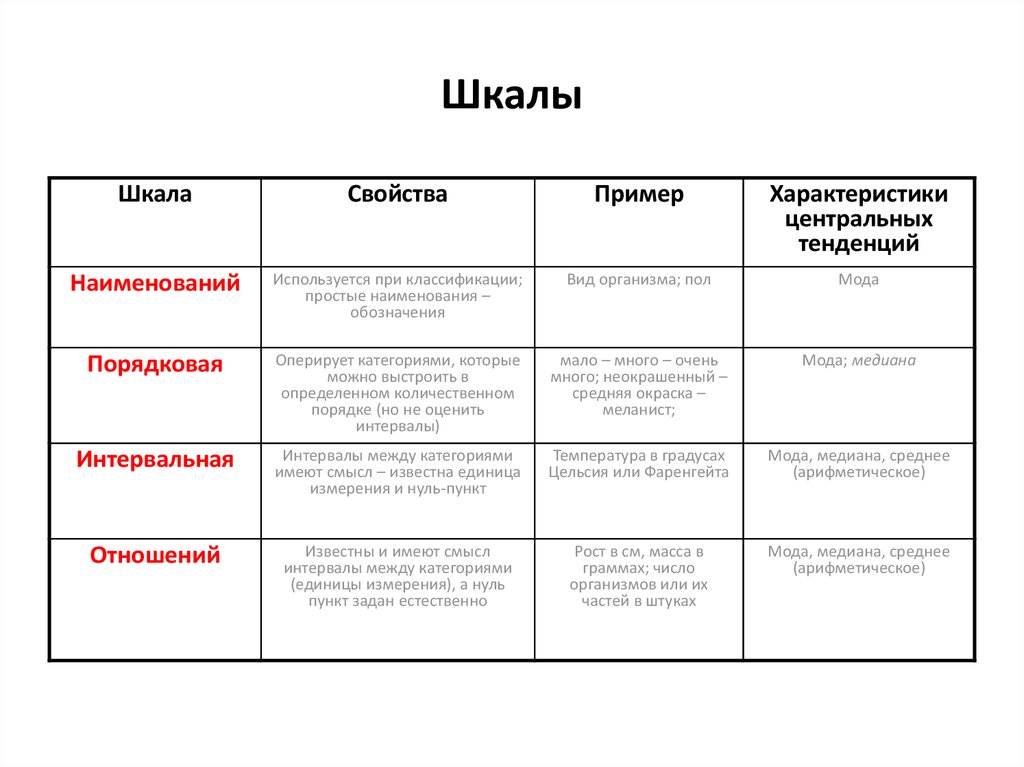
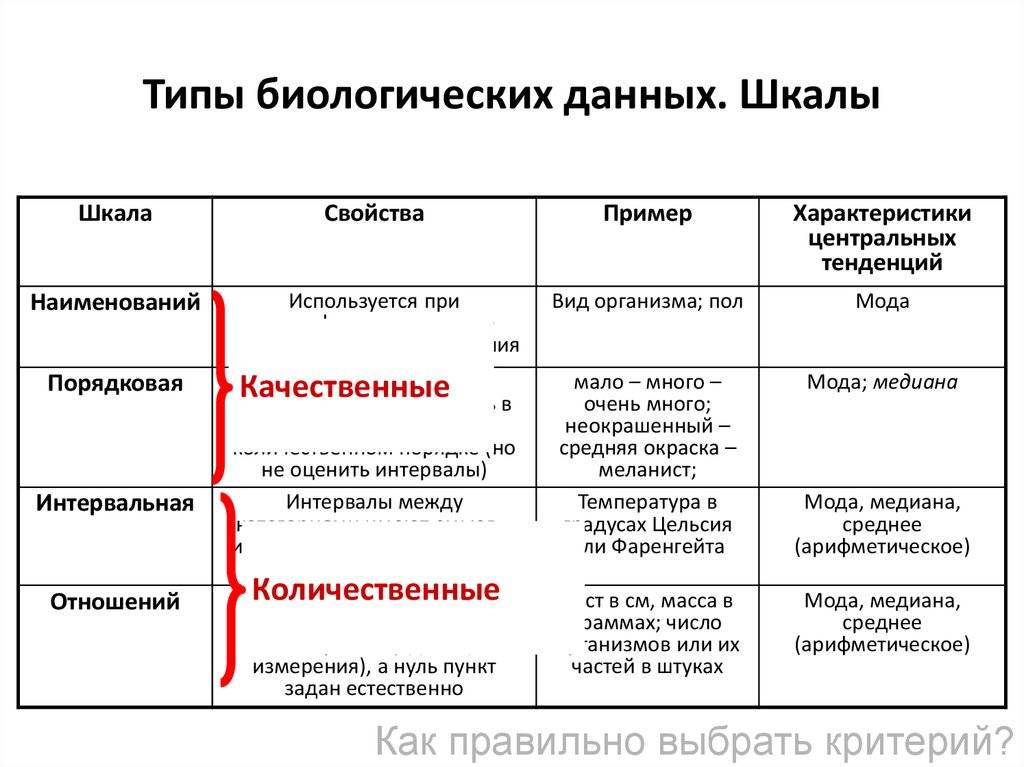
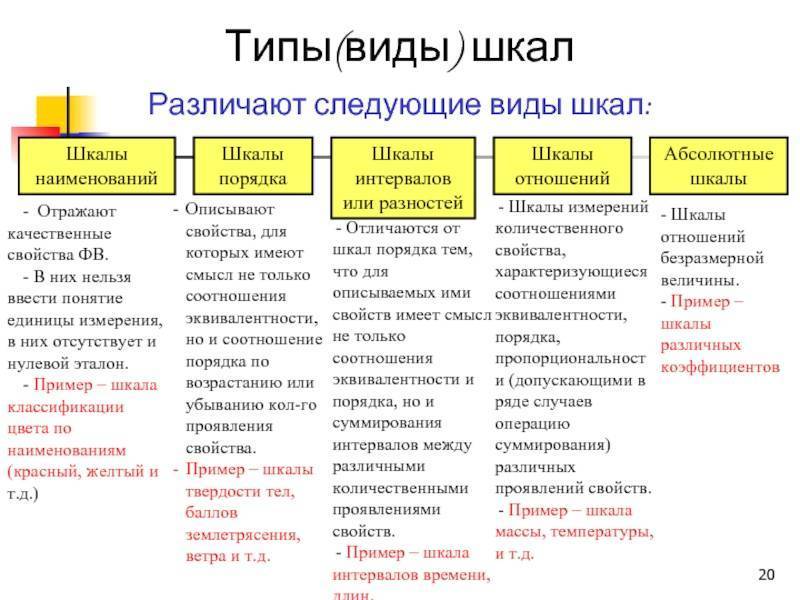
Статистические шкалы можно разделить на качественные и количественные. К качественным шкалам относится номинальная и порядковая шкалы. К количественным – интервальная шкала и шкала отношений.
Номинальная шкала – качественная шкала. Относится к самому элементарному типу измерения. В ней каждому оцениваемому объекту приписывается наименование или число.
Пример 1: Признак – пол. Цифрой «0» обозначаем женщин, цифрой «1» — мужчин. Очевидно, что расчет среднего арифметического не иимеет смысла.
Пример 2: Признак — Цвет волос: Цифрой «1» обозначаем брюнетов, цифрой «2» — шатенов, цифрой «3» – блондинов, цифрой «4» – людей, имеющих рыжий цвет волос.
Пример 3: Номера на футболках спортсменов.
Более подробно о методах статистической обработки данных рассказано в книгах:
- Факторный анализ в педагогических исследованиях в области физической культуры и спорта
- Компьютерная обработка данных экспериментальных исследований
- Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта
Для области физической культуры и спорта использование номинальной шкалы очень важно, так как очень часто используется метод анкетного опроса. При этом результаты представлены в виде таблицы, в которой представлена абсолютная частота ответов на тот или иной вопрос (табл. 1)
1).
Таблица 1
Оценка мужчинами и женщинами своего психического состояния
| Психическое состояние | Мужчины | Женщины | Всего |
| Крайне неустойчивое | 3 | 16 | 19 |
| Неустойчивое | 22 | 18 | 40 |
| Устойчивое | 32 | 9 | 41 |
| Очень устойчивое | 5 | 1 | 6 |
| Всего | 62 | 44 | 100 |
Порядковая шкала (ранговая) – качественная шкала, использующая свойство чисел отражать отношение «больше – меньше».
В порядковой шкале нельзя сказать насколько или во сколько одно значение больше другого, но можно сказать какое больше, какое меньше. Очень часто статистические данные, представленные в порядковой шкале, измеряются в баллах.
Интервальная шкала – количественная шкала. В этой шкале устанавливается единица измерения.
В интервальной шкале, например, измеряется температура (по Цельсию или по Фаренгейту).
Шкала отношений. Для признаков, измеренных в шкале отношений можно дополнительно сказать: во сколько одно значение больше другого. Шкала отношений в отличие от интервальной шкалы обладает точкой нулевого отсчета.
Примерами статистических данных, представленных в шкале отношений являются признаки: рост, вес, температура по Кельвину.
Более подробное эта тема рассмотрена в литературе, ссылки на которую приведены ниже.
Литература
- Барникова, И.Э. Информационные технологии в обработке анкетных данных в педагогике и биомеханике спорта: учеб. пособие / И.Э. Барникова; А.В. Самсонова; Национальный государственный университет физической культуры, спорта и здоровья им. П.Ф. Лесгафта, Санкт–Петербург. – СПб.: , 2017. – 103 с.
- Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.