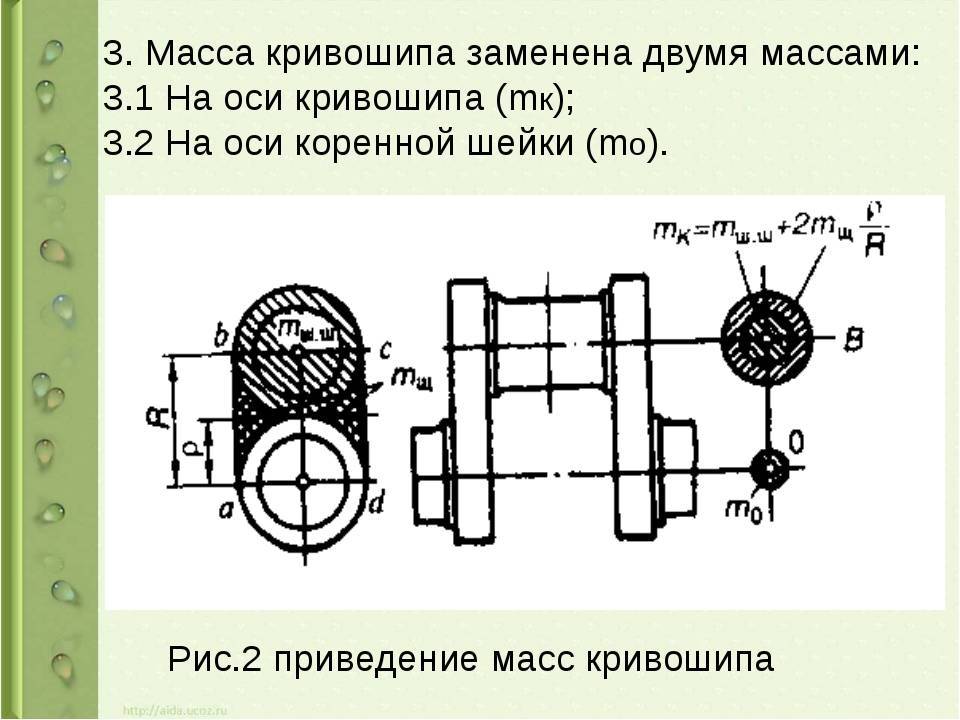
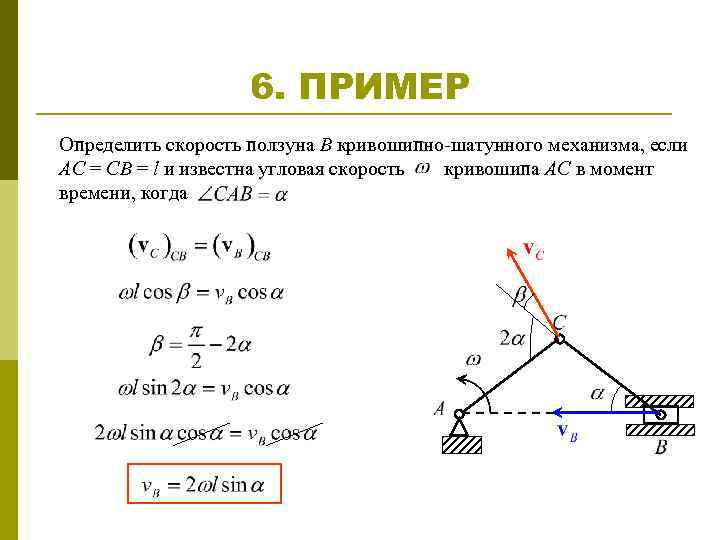
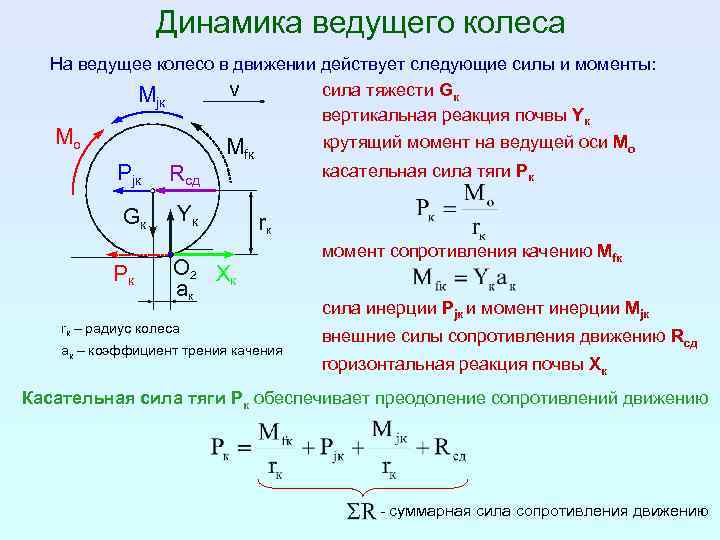
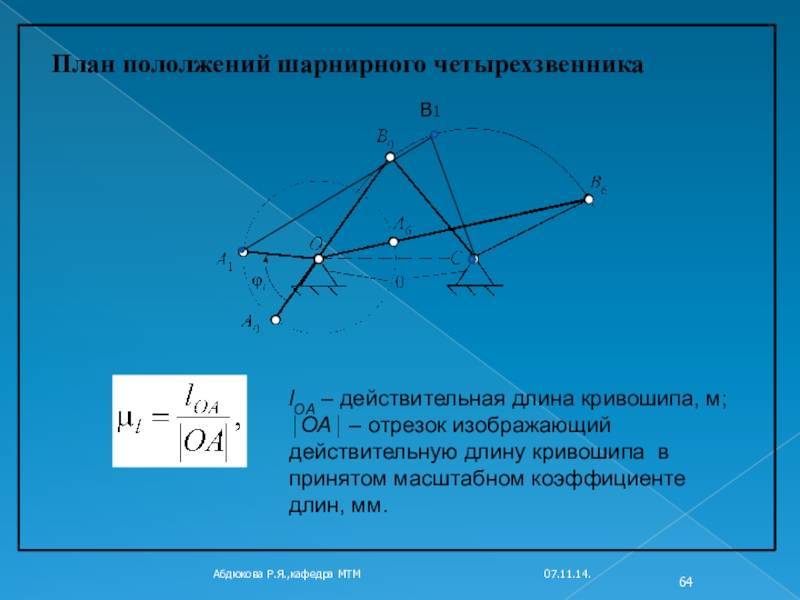
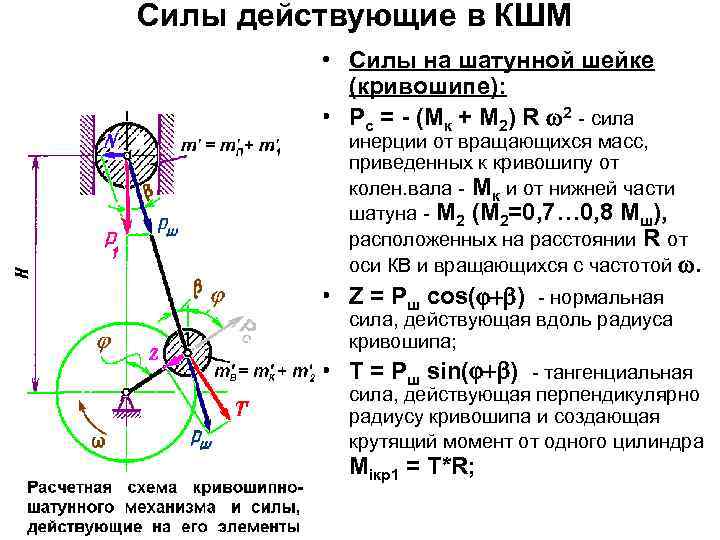
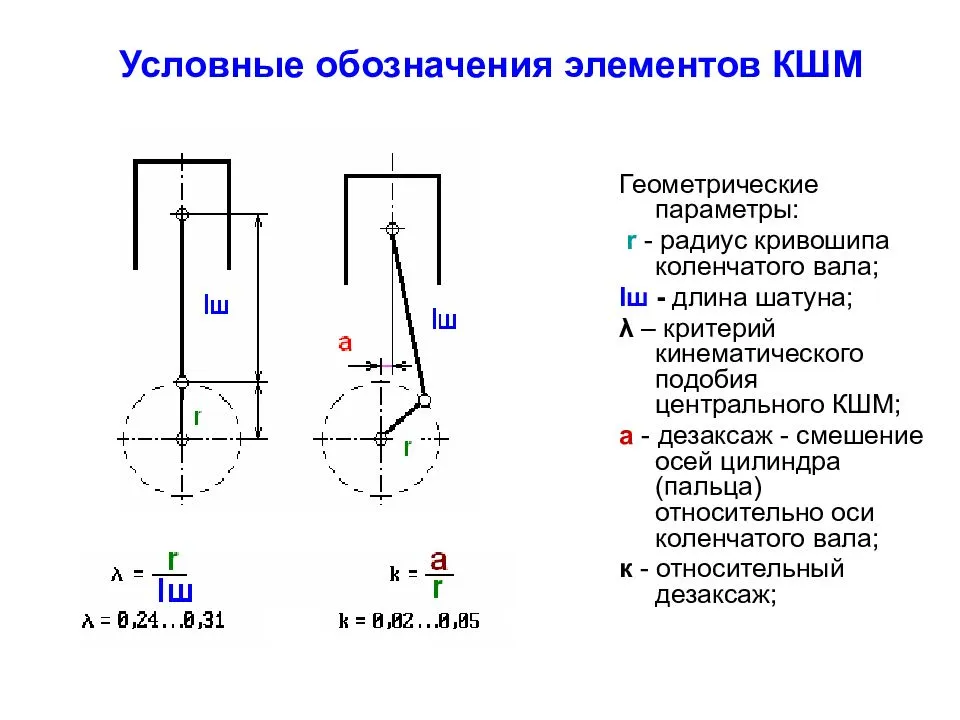
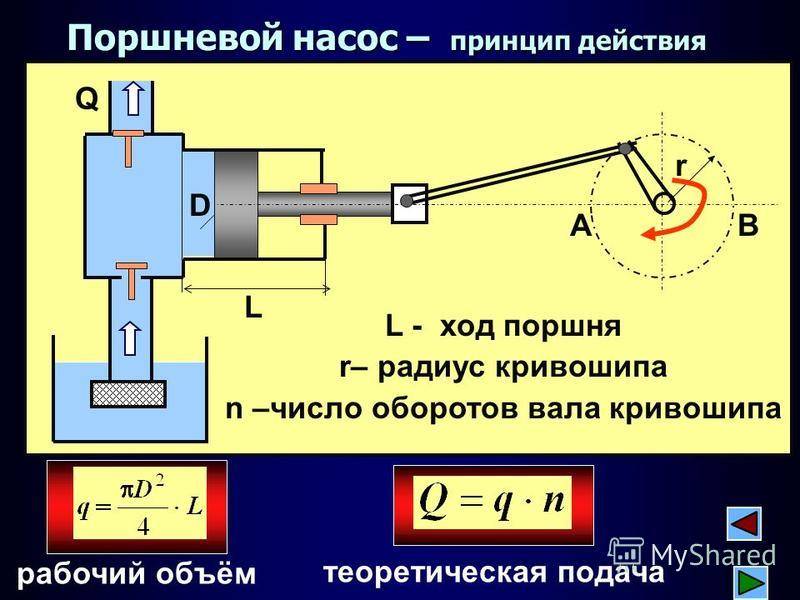
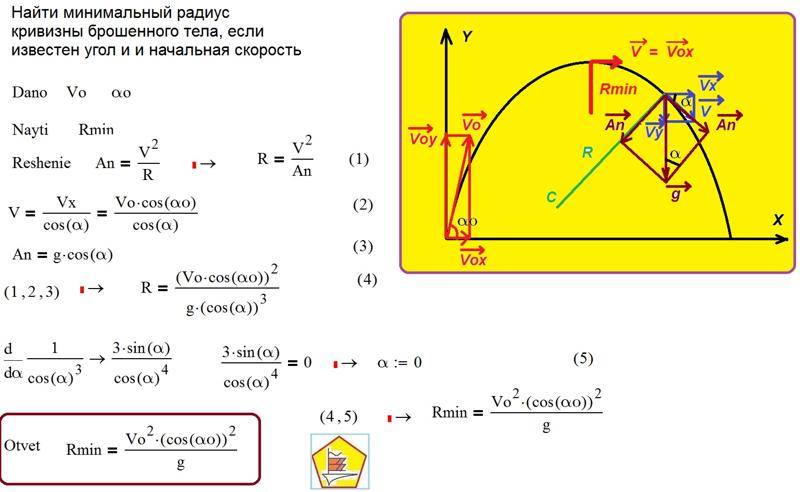
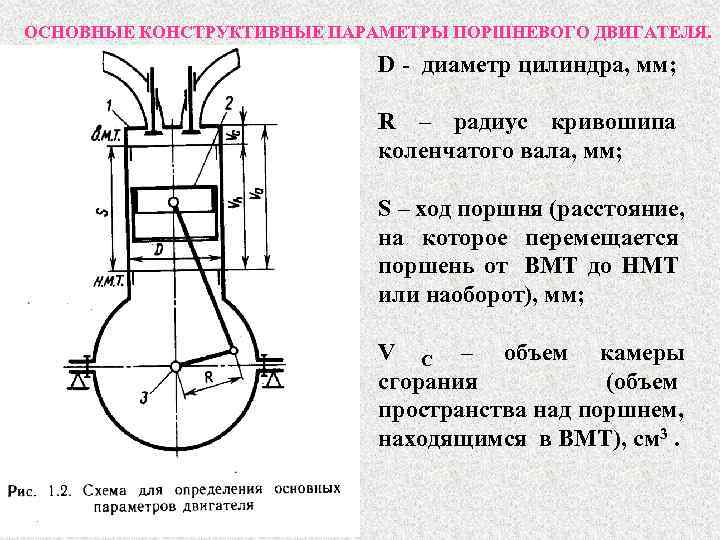
Выбор размеров и числа цилиндров
Выбор размеров и числа цилиндров производится на основе следующих соображений.
Диапазон возможного изменения диаметра цилиндра можно определить, используя зависимость D = f(nн) для существующих моделей двигателей. Точки на графиках соответствуют реальным двигателям, степень концентрации точек указывает предпочтительность выбора размеров цилиндра при заданной частоте вращения. Верхние границы заштрихованной области относятся к короткоходным (S/D = 0,8…0,9), а нижние — к длинноходным (S/D = 1,1…1,2) двигателям. При известных типах двигателя и частоте вращения можно определить диапазон предпочтительных диаметров цилиндра. Назначив стандартный D (в мм, округленный на 0 или 5 — для дизелей или до ближайшего четного числа — для карбюраторных двигателей), по соответствующему соотношению S/D определяют ход поршня S и ориентировочно среднюю скорость поршня.
Из исходных данных . Принимаем D=140 мм. По соотношению 1,08 определяем ход поршня S (расстояние по оси цилиндра между мёртвыми точками) и ориентировочно среднюю скорость поршня.
Среднюю скорость поршня определяем по формуле:
Следует помнить, что Сn является показателем тепловой напряжённости и динамической нагруженности деталей двигателя и существенное её повышение.
По заданным номинальной мощности , частоте вращения коленчатого вала , оценённым размером цилиндра определяем их число .
Число цилиндров в свою очередь определяется уровнем форсирования двигателя по мощности, т. е. литровой мощностью.
Для определения литровой мощности целесообразно использовать графики Nел=f(D) (рисунок 1.2) . Согласно графику пределы литровой мощности находятся в интервале .
Устанавливаем цилиндровую мощность:
Рабочий объём цилиндра, это объём цилиндра, освобождаемый поршнем при перемещении от в.м.т. к н.м.т.
Значение D и S — принимаем в дм.
Требуемое число цилиндров определяем по формуле:
Полученное значение округляем до ближайшего целого числа, однако желательно исключить значения . Принимаем .
Необходимо уточнить значение литровой мощности по формуле:
Свойства радиуса
В отношении радиуса действуют несколько важных правил:
- Радиус составляет половину диаметра. Это мы продемонстрировали только что.
- У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.
- Если в точке пересечения радиуса с поверхностью окружности провести касательную, то эти две линии будут пересекаться под прямым углом. Доказательство этой теоремы наглядно приводится на следующем рисунке.
- Радиус, который перпендикулярен хорде, делит ее на две равные части.Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.
Визуальный шинный калькулятор
Когда изнашиваются заводские шины или просто хочется поставить другие колеса, то возникает вопрос: а какие размеры шин подойдут моей машине? Дело в том, что каждый автомобиль рассчитан под определенный диаметр колес и ширину протектора. Обычно, данная информация содержится на оборотной стороне крышки бензобака или в документах по эксплуатации. Если отклониться от этих типоразмеров больше чем на 2-3 процента, то расход бензина вырастет, спидометр начнет врать, а в случае большой разницы вождение может стать просто опасным.
Но как подобрать шины правильного размера, если на профиле написаны какие-то непонятные цифры? Не измерять же их линейкой, ей богу. Именно для этих целей и создан данный шинный калькулятор. Он позволяет определить разницу между шинами в сантиметрах, дюймах и процентах. В частности, с помощью шинного калькулятора вы можете рассчитать и сравнить диаметр шины, ширину протектора, высоту профиля и окружность. Дополнительно, калькулятор определяет потенциальные различия в показателях скорости на спидометре, изменения клиренса и разницу в количестве оборотов на один километр (или милю).
Калькулятор отображает визуальную разницу в диаметре, профиле, клиренсе и ширине шины. В правой части генерируется динамический рисунок колес, с пунктирной схемой и параметрами. В верхней части находится визуальное представление старой шины (оригинального типоразмера), а в нижней части отрисовывается ваша потенциальная новая шина. Рисунок отображается в двух проекциях: боковой и фронтальной. И ту и другую можно скачать на компьютер в формате png. Для этого нажмите на картинку правой кнопкой и выберите «Сохранить как. «.
Выбор отношения радиуса кривошипа к длине шатуна
Отношение радиуса кривошипа к длине шатуна л = R/L для современных автотракторных двигателей составляет 0,21…0,30, причем для быстроходных двигателей обычно применяются длинные шатуны (значения л малы), для тракторных — относительно короткие.
Следует учитывать, что с увеличением л повышается вероятность задевания шатуна за нижнюю кромку цилиндра, в связи с чем приходится выполнять вырезы в нижней части цилиндров; увеличивается давление на стенку цилиндра, повышаются потери мощности на трение и ускоряется изнашивание цилиндров и поршней; возрастают силы инерции второго порядка, что также способствует ускорению изнашивания деталей двигателя; уменьшается габаритная высота, масса шатуна и двигателя. Последнее является единственным преимуществом коротких шатунов.
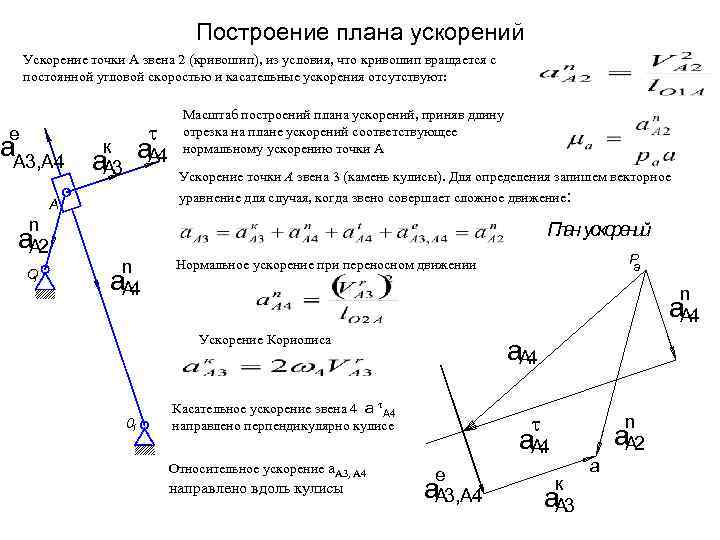
6.4 Определение ускорения поршня
Уравнение ускорения поршня может быть получено дифференцированием уравнения скорости по t.
При
Вывод:
а) При φ=180°; и λ<0,25 кривая ускорения выпуклая и ускорение имеет одно наименьшее значение
б) При λ>0,25 в точке кривая ускорения имеет вогнутость в сторону оси и ускорение дважды достигает наименьшего значения
Построение кривой ускорения поршня произведено:
а) аналитически. При этом значение множителя Aj в скобках справочная величина в зависимости от λ и φ.
б) графически. Путем сложения ускорения первого jП I=ω2Rcosφ и второго jП II=ω2Rλcos2φ
Для дезаксиального механизма jП
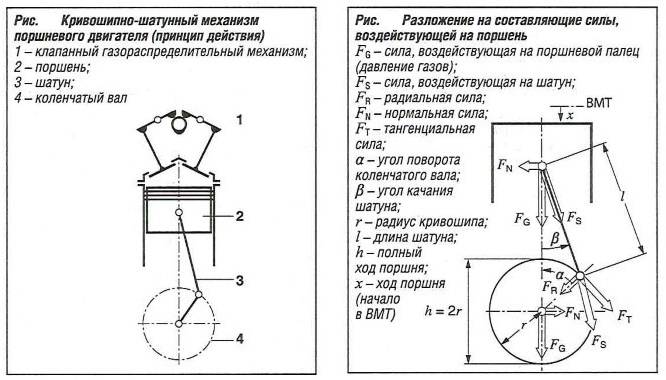
Описание и терминология
График ссылок {*}
Система шатун-кривошип позволяет преобразовать линейное движение конца шатуна в непрерывное вращательное движение, доступное для кривошипа ( коленчатого вала ), и наоборот. Он состоит из 4 основных частей:
- рамы (1).
- кривошипа (2), также называемый коленчатый вал на двигателях,
- соединительный стержень (3),
- Эффектор (4): поршень , рычаг, педали в зависимости от случая,
Система обычно дополняется маховиком, стабилизирующим скорость вращения кривошипа.
Паровая машина, шток соединен с поршнем по прямолинейной траектории.
Движение на половину вращения, звено соединено с другим кривошипом
Кривошип и исполнительный элемент составляют две входные-выходные части механизма.
Кривошип (приводной или принимающий) приводится в движение непрерывным вращательным движением , в то время как исполнительный элемент приводится в движение переменным линейным движением, прямолинейным или нет. Шатун имеет два сочленения: с одной стороны на кривошип, а с другой – на эффектор. В зависимости от типа соединения, наложенного на эффектор, система выполняет следующие преобразования движения:
Непрерывное вращение возвратно-поступательное прямолинейное движение.⇔{\ displaystyle \ Leftrightarrow}
Это тот случай, когда конец шатуна прикреплен к поршню, подвижному в цилиндре, или, в более общем смысле, к скользящему соединению. Конец шатуна описывает прямой отрезок. Примеры:
- направление двигателя : тепловая машина, паровая машина.
- Направление приема : гидростатический насос, компрессор, пильный станок, швейная машина (движение иглы), перфоратор.
Непрерывное вращение переменное вращение.⇔{\ displaystyle \ Leftrightarrow}
Это тот случай, когда конец шатуна соединен с другим кривошипом, педалью или шарнирным рычагом. Конец шатуна описывает круговой сегмент кривой. Примеры:
- направление мотора : педальное устройство, детская коляска, швейная машинка (тренировочная), прялка.
- направление приемника : альтернативный роторный насос, стеклоочиститель, автоматический шлагбаум, транспортер.
и вообще любой четырехстворчатый механизм
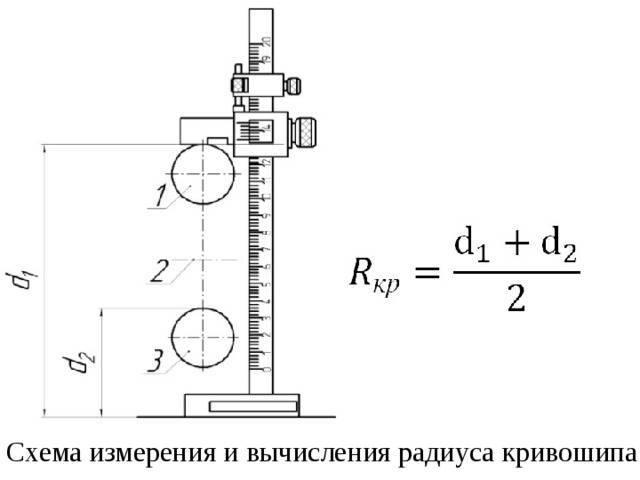
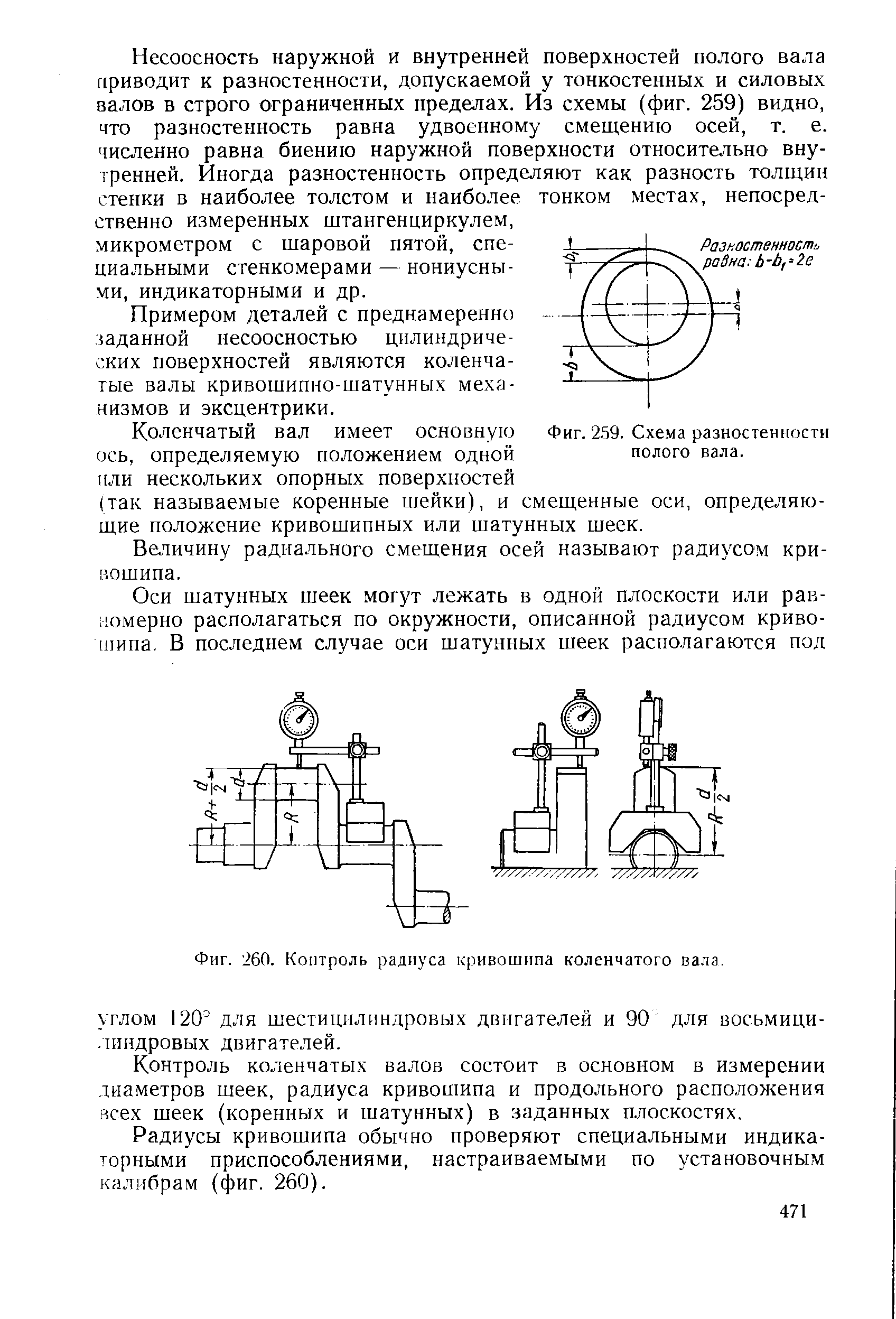
Как определить радиус кривошипа
Номинальное усилие без учета сил трения и с учетом сил трения рассчитываются соответственно по зависимостям
где — приведенное плечо сил трения кривошипно-шатунного механизма, мм
На рисунке 2 приведен нагрузочный график
Рисунок 2- Нагрузочный график
На рисунке 4 приведен график зависимости крутящего момента от угла поворота кривошипа
Рисунок 3-График зависимости крутящего момента от угла поворота кривошипа
ОПЕРАЦИЯ — ГИБКА c ВЫРУБКОЙ
номинальное усилие пресса, — 3150.000
коэффициент дезаксиальности — 0.000
коэффициент длины шатуна — 0.100
диаметр вала в опорах, — 230.000
¦ ХОД, мм ¦ УГОЛ, гр. ¦ Мкр, кН*м ¦ ПРИВЕДЕННОЕ¦ УСИЛИЕ, кН ¦
¦ 34.677 ¦ 47.149 ¦ 0.000¦ 86.404 ¦ 0.000¦
¦ 28.542 ¦ 42.490 ¦ 50.826¦ 80.677 ¦ 630.000¦
¦ 19.217 ¦ 34.524 ¦ 70.116¦ 69.559 ¦ 1008.000¦
¦ 3.135 ¦ 13.722 ¦ 21.642¦ 34.353 ¦ 630.000¦
¦ 0.000 ¦ -0.000 ¦ 26.299¦ 8.349 ¦ 3150.000¦
¦ 0.000 ¦ -4.353 ¦ 27.957¦ 16.694 ¦ 1674.736¦
РАБОТА ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ,
(график Усилие-Путь) — 25308.52
РАСХОД ЭНЕРГИИ НА СОВЕРШЕНИЕ ПРЕССОМ РАБОЧЕГО ХОДА,
( по графику крутящих моментов) — 35130.94
Номинальный угол, — 34.00000
Номинальный крутящий момент, — 216.70609
Номинальное плечо крутящего момента, — 68.79558
Источник статьи: http://intehstroy-spb.ru/tehnologii/1-2-opredelenie-radiusa-krivoshipa-i-dliny-shatuna.html
Изменение объема камеры сжатия
Альтернативные способы изменения объема камеры сжатия главным образом сводятся к устройству разделенной камеры, состоящей из двух сообщающихся частей – основной и дополнительной. Объем дополнительной камеры варьируется перемещением ее свода, которое осуществляется гидравлическими, механическими или электрическими устройствами. При этом изменяется суммарный объем камеры сгорания и соответственно степень сжатия.
Одной из первых подобную систему освоила французская фирма Hispano-Suiza. В авиационном дизельном двигателе V8 модели HS-103 применяли вихревую камеру переменного объема, подвижный свод которой перемещался под действием гидравлики. Похожее устройство регулирования степени сжатия в искровом двигателе было запатентовано концерном Ford. Отличие состояло в том, что в этой конструкции подвижная часть дополнительной камеры перемещалась при помощи профилированного кулачка. Наконец, по этому же принципу варьировалась степень сжатия в концепт-двигателе ALVAR, авторство которого принадлежит концерну Volvo. Здесь сводами дополнительных камер сжатия служили днища небольших вторичных поршней, которые приводились в действие от вала, расположенного в ГБЦ.

Способ разделения камеры сжатия привлекателен тем, что необходимые изменения ограничиваются только конструкцией головки. С другой стороны, ГБЦ (особенно современного многоклапанного двигателя) и без того достаточно плотно «упакована». Так что размещение в ней дополнительного элемента представляет большую проблему. Наличие «аппендикса» в камере сгорания неизбежно нарушает процесс смесеобразования и сгорания, что приводит к ухудшению экологических характеристик мотора. Наконец, регулирующий механизм работает в зоне максимальных тепловых и механических нагрузок, что не может не сказаться на его надежности.
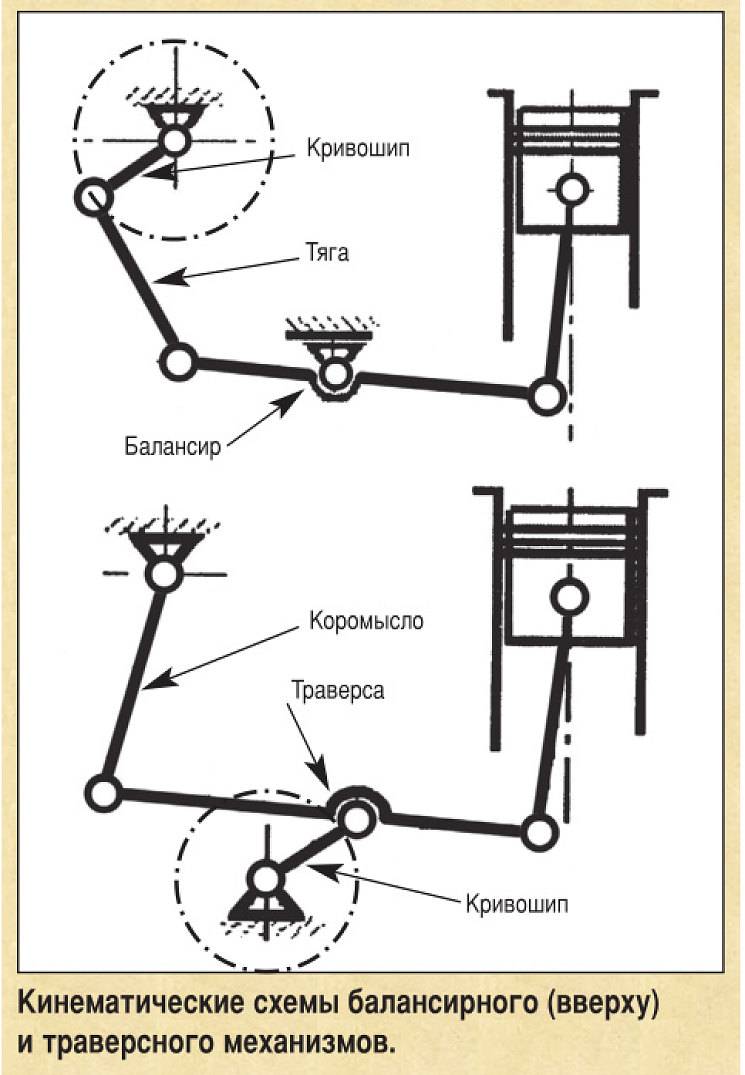
На этом этапе можно сделать некоторые промежуточные выводы. Они, к сожалению, не очень утешительны. Для двигателей с традиционным КШМ были предложены и в различной степени опробованы всевозможные варианты регулирования степени сжатия. Большинство из них позволяло решить поставленную задачу по изменению ε, но ни один не оказался безусловно предпочтительным и пригодным для широкого применения на серийных моторах из-за трудностей в изготовлении или обеспечении приемлемой работоспособности. Это побудило инженеров-двигателистов вспомнить о других типах механизмов, преобразующих поступательное движение во вращение.
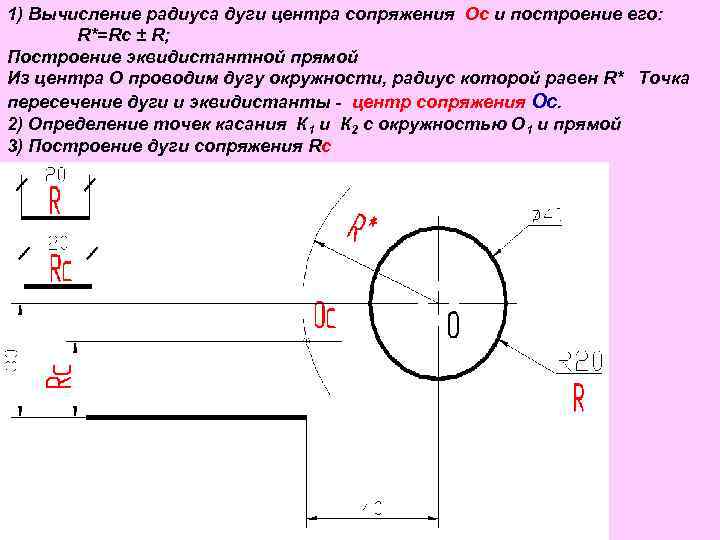
Первый метод определения радиуса дуги или сегмента круга
Изначально это выглядит так:
Рисунок 463.1. а) имеющаяся дуга, б) определение длины хорды сегмента и высоты.
Таким образом, когда имеется дуга, мы можем соединить ее концы и получим хорду длиной L. Посредине хорды мы можем провести линию, перпендикулярную хорде и таким образом получим высоту сегмента H. Теперь, зная длину хорды и высоту сегмента, мы можем сначала определить центральный угол α, т.е. угол между радиусами, проведенными из начала и конца сегмента (на рисунке 463.1 не показаны), а затем и радиус окружности.
Решение подобной задачи достаточно подробно рассматривалось в статье “Расчет арочной перемычки”, поэтому здесь лишь приведу основные формулы:
tg(a/4) = 2Н/L (278.1.2)
тогда
а/4 = arctg(2H/L)
R = H/(1 – cos(a/2)) (278.1.3)
Как видим, с точки зрения математики никаких проблем с определением радиуса окружности нет. Данный метод позволяет определить значение радиуса дуги с любой возможной точностью. Это главное достоинство данного метода.
А теперь поговорим о недостатках.
Проблема данного метода даже не в том, что требуется помнить формулы из школьного курса геометрии, успешно забытые много лет назад – для того, чтобы напомнить формулы – есть интернет. А вот калькулятор с функцией arctg, arcsin и проч. есть далеко не у каждого пользователя. И хотя эту проблему также успешно позволяет решить интернет, но при этом не следует забывать, что мы решаем достаточно прикладную задачу. Т.е. далеко не всегда нужно определить радиус окружности с точностью до 0.0001 мм, точность 1 мм может быть вполне приемлема.
Кроме того, для того, чтобы найти центр окружности, нужно продлить высоту сегмента и отложить на этой прямой расстояние, равное радиусу. Так как на практике мы имеем дело с не идеальными измерительными приборами, к этому следует прибавить возможную погрешность при разметке, то получается, что чем меньше высота сегмента по отношению к длине хорды, тем больше может набежать погрешность при определении центра дуги.
Опять же не следует забывать о том, что мы рассматриваем не идеальный случай, т.е. это мы так сходу назвали кривую дугой. В действительности это может быть кривая, описываемая достаточно сложной математической зависимостью. А потому найденный таким образом радиус и центр окружности могут и не совпадать с фактическим центром.
В связи с этим я хочу предложить еще один способ определения радиуса окружности, которым сам часто пользуюсь, потому что этим способом определить радиус окружности намного быстрее и проще, хотя точность при этом значительно меньше.
Маятник Капицы
Обычный маятник, если перевернуть его кверху ногами, неустойчив. Для него крайне трудно найти верхнюю точку равновесия. Но если совершать быстрые вертикальные возвратно-поступательные колебания, то положение такого маятника становится устойчивым.
Петр Леонидович Капица
Советский академик и нобелевский лауреат по физике Петр Леонидович Капица (1894 — 1984) использовал модель маятника с вибрирующим подвесом для построения новой теории, которая описывала эффекты стабилизации тел или частиц. Работа Капицы по стабилизации маятника была опубликована в 1951 году, а сама модель получила название «маятник Капицы». Более того, было открыто новое направление в физике — вибрационная механика. Данная модель позволила наглядно показать возможности высокочастотной электромагнитной стабилизации пучка заряженных частиц в ускорителях.
Владимир Игоревич Арнольд
Другой советский математик и академик Владимир Игоревич Арнольд (1937-2010), который был заместителем Капицы, вспоминал его слова:
«Он (Капица — примечание) сказал: «Вот смотрите — когда придумывается какая-то физическая теория, то прежде всего надо сделать маленький какой-нибудь прибор, на котором его наглядно можно было-бы продемонстрировать кому угодно. Например, Будкер и Векслер хотят делать ускорители на очень сложной системе. Но я посмотрел, что уравнения, которые говорят об устойчивости этого пучка, означают, что если маятник перевернут кверху ногами, он обычно неустойчив, падает. Но если точка подвеса совершает быстрые вертикальные колебания, то он становится устойчивым. В то время как ускоритель стоит много миллионов, а этот маятник можно очень легко сделать. Я его сделал на базе швейной электрической машинки, он вот здесь стоит». Он нас отвел в соседнюю комнату и показал этот стоящий вертикально маятник на базе швейной машинки».
Демонстрация динамической стабилизации перевернутого маятника с помощью электробритвы
У математика Арнольда не было своей швейной машинки, и он огорчился. Но у него была электробритва «Нева», из которой и был собран перевернутый маятник. К сожалению, в первой конструкции маятник падал. Тогда Арнольд вывел формулу и увидел, что длина маятника не должна быть больше 12 сантиметров. Известный математик укоротил подвес до 11 сантиметров и все получилось.
Давайте посмотрим, какие силы действуют на «маятник Капицы». После прохождения верхней мертвой точки подвес маятника начинает тянуть грузик вниз. После прохождения нижней мертвой точки подвес толкает грузик вверх. Так как углы вежду векторами сил в верхней и нижней точке разные, то сумма их векторов дает силу, направленную к оси вертикальных колебаний маятника. Если эта сила больше силы тяжести, то верхнее положение маятника становится устойчивым.
А эта формула описывает взаимосвязь частоты вибраций подвеса, амплитуды колебаний и длины жесткого подвеса.
Видео:
- GetAClass. Маятник Капицы
- Маятник Капицы: диалог академика Арнольда и Капицы, вывод формулы
Как определить радиус кривошипа
Номинальное усилие без учета сил трения и с учетом сил трения рассчитываются соответственно по зависимостям
где — приведенное плечо сил трения кривошипно-шатунного механизма, мм
На рисунке 2 приведен нагрузочный график
Рисунок 2- Нагрузочный график
На рисунке 4 приведен график зависимости крутящего момента от угла поворота кривошипа
Рисунок 3-График зависимости крутящего момента от угла поворота кривошипа
ОПЕРАЦИЯ — ГИБКА c ВЫРУБКОЙ
номинальное усилие пресса, — 3150.000
коэффициент дезаксиальности — 0.000
коэффициент длины шатуна — 0.100
диаметр вала в опорах, — 230.000
¦ ХОД, мм ¦ УГОЛ, гр. ¦ Мкр, кН*м ¦ ПРИВЕДЕННОЕ¦ УСИЛИЕ, кН ¦
¦ 34.677 ¦ 47.149 ¦ 0.000¦ 86.404 ¦ 0.000¦
¦ 28.542 ¦ 42.490 ¦ 50.826¦ 80.677 ¦ 630.000¦
¦ 19.217 ¦ 34.524 ¦ 70.116¦ 69.559 ¦ 1008.000¦
¦ 3.135 ¦ 13.722 ¦ 21.642¦ 34.353 ¦ 630.000¦
¦ 0.000 ¦ -0.000 ¦ 26.299¦ 8.349 ¦ 3150.000¦
¦ 0.000 ¦ -4.353 ¦ 27.957¦ 16.694 ¦ 1674.736¦
РАБОТА ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ,
(график Усилие-Путь) — 25308.52
РАСХОД ЭНЕРГИИ НА СОВЕРШЕНИЕ ПРЕССОМ РАБОЧЕГО ХОДА,
( по графику крутящих моментов) — 35130.94
Номинальный угол, — 34.00000
Номинальный крутящий момент, — 216.70609
Номинальное плечо крутящего момента, — 68.79558
Источник статьи: http://intehstroy-spb.ru/tehnologii/1-2-opredelenie-radiusa-krivoshipa-i-dliny-shatuna.html
Введите значения H и h в миллиметрах
Не забывайте, что для гибки профилей необходим технологический припуск от 500 до 1000 мм. на заготовку.
Статья написана в ответ на запрос пользователя, который хотел вычислять глубину прогиба профиля ведущим валом, для получения изогнутой трубы с заданными параметрами. До запроса я даже и не знал, что есть специальные машины для холодной гибки труб. Причем бывают как и промышленные гибочные станки, так и ручные гидравлические трубогибы.
Все они действуют по одному принципу, который можно понять, посмотрев на картинку.
Профиль (труба) укладывается между валиками, затем центральный валик с усилием прогибает профиль, и дальше оставшийся кусок прокатывается через станок.
С моей дилетантской точки зрения, процесс выглядит примерно так

Или, если совместить:

Собственно, интересует вопрос — насколько надо прогнуть трубу, то есть опустить ведущий вал, чтобы после прокатки всего отрезка профиля получить заданный изгиб? Изгиб трубы, очевидно, задается радиусом. Но, как показал запрос пользователя, параметры могут быть заданы не только радиусом, но и длиной и высотой хорды, если надо получить арку. Здесь нам пригодится калькулятор, который по заданной длине (C) и высоте хорды (h) рассчитывает длину требуемого отрезка (L) и радиус окружности (R) — смотри рисунок.
Параметры сегмента по хорде и высоте
Подробности и формулы смотри здесь — Сегмент круга
Идем дальше. Итак, нам нужно получить глубину прогиба зная радиус, расстояние между ведомыми валиками, радиус валиков и размеры профиля. Перерисуем совмещенный рисунок, добавив несколько нужных линий, и убрав все ненужные.

Точка B — центр нашей окружности
Обратите внимание, что расчет идет по внешнему по отношению к изгибу краю профиля. Поскольку радиус по высоте и ширине хорды скорее всего будет рассчитываться по оси профиля, к полученному радиусу надо прибавить радиус профиля так, чтобы получить радиус внешнего края профиля. Дальше в ход идет геометрия
Из расстояния AC и расстояния AB находим угол ABD
Дальше в ход идет геометрия. Из расстояния AC и расстояния AB находим угол ABD.
При монтаже трубопроводов из различного вида материалов его изгиб позволяет уменьшить количество разборных или сварных соединений, понижающих надежность магистрали. При проведении трубогибочных работ полезно знать допустимый радиус гиба трубы, обеспечивающий безопасность и надежную эксплуатацию трубопроводной системы в соответствии с технической документацией.
Чаще всего изгибаемые трубы выполнены из стали и коррозионно-стойких металлов: нержавейки, меди, алюминия, латуни, при устройстве бытовых систем отопления и водопроводов изгибают изделия из пластика и металлопластика. Методы сгибания труб по радиусу различны в зависимости от материала их изготовления и могут быть выполнены ручным или электромеханическим способом на специальных станках.
Какие детали двигателя определяют ход поршня?
Ход поршня — это расстояние между верхней и нижней мертвыми точками поршня. Он определяется радиусом кривошипа коленчатого вала.
Радиус кривошипа — это расстояние между осевой линией вращения коленчатого вала и осевой линией шатунной шейки. Радиус кривошипа равен половине хода поршня.
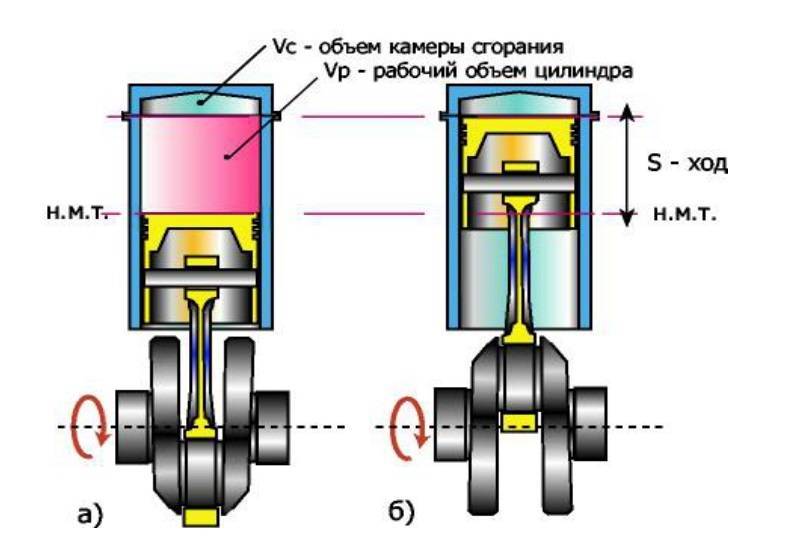
В случае замены коленчатого вала другим, имеющим больший ход, верхняя мертвая точка хода поршней может оказаться над верхней плоскостью (плитой) блока цилиндров. Решить эту проблему можно, установив новые поршни, на которых поршневые пальцы стоят выше. Еще один возможный вариант — заменить шатуны более короткими, чтобы уменьшить максимальную высоту подъема поршней в цилиндрах.
При изменении длины шатуна ход поршня не изменяется, изменяется только положение мертвых точек хода поршня.
Сразу приведу список используемой литературы во избежании гнета в мой адрес

Давненько меня тревожит тема правдивости R/S и влияния этого отношения на поведение двигателя.Начитался кучу бреда на драйве о бесполезности данного коэффициента, об необоснованных расчетах и тд.В тырнете гуляет одна статья, в которой говориться, что “золотая средина R/S 1,75 и тд” и что длинный шатун лучше для высокооборотистого двигателя. В свою очередь, уважаемый многими Травников утверждает, что R/S не более чем миф, хотя верить ему в плане теории это гиблое дело.Пришлось вспомнить третий курс и немного погрузиться в расчеты кинематики Кривошипно Шатунного Механизма(далее КШМ).
Все расчеты я произвел на примере двух двигателей: F20b и F22b, которые хондовские. На мой взгляд для наглядного сравнения они подходят как нельзя кстати.Итак, в совковой литературе отсутствует такое понятие как rode to stroke, у нас применялось немного другое понятие — безразмерный параметр КШМ(отношение радиуса кривошипа к длине шатуна) — но суть от этого ничуть не изменилась.
λ = r/Lгде r — радиус колевала(кривошипа), L — длинна шатуна.Для F20b получаем λ=0,044/145=0,303Для F22b получаем λ=0,0475/141,5=0,335
В литературе четко прописано

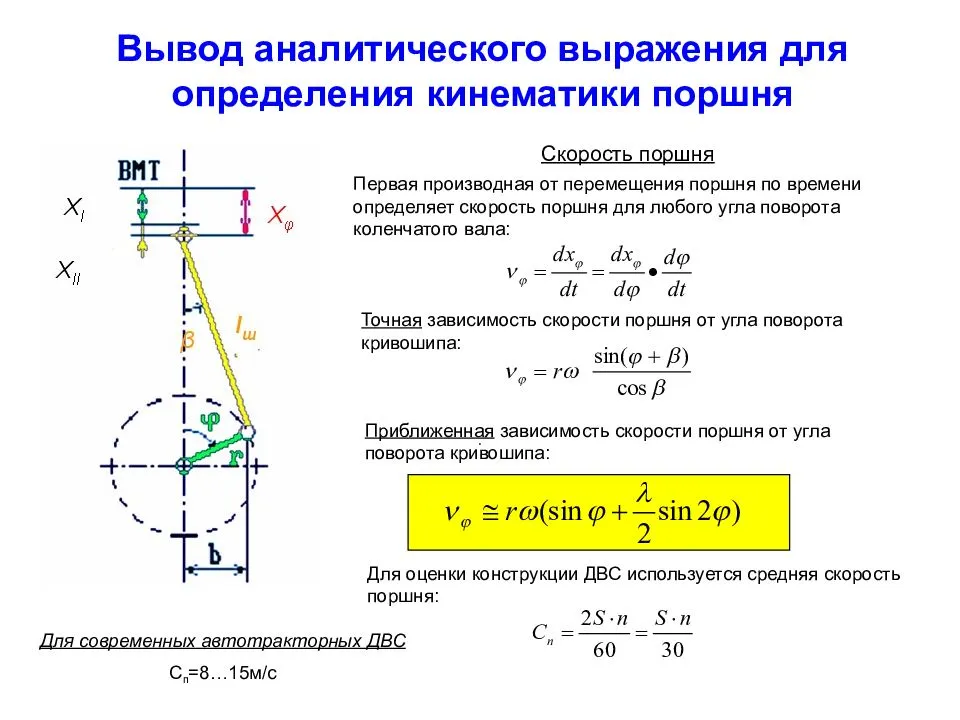
Если рассуждать логически, то чем больше скорость, тем больше износ и потери на трение, но средняя скорость не обусловлена длинной шатуна, она зависит лишь от радиуса коленвала и оборотов двигателя.Куда более интересные для нас параметры это скорость поршня в определенный момент времени(угол поворота коленчатого вала) и его ускорение.


Где ϕ — угол поворота коленчатого вала в градусах.Зависимость от длинны шатуна присутствует в обеих формулах, я не стану расписывать решение пошагово. Все равно считал все в Екселе. Покажу сразу график
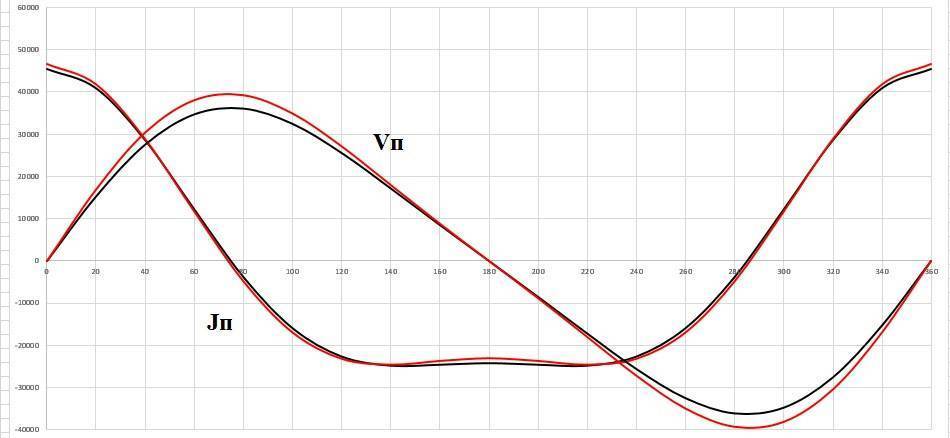
На графике видно, что скорость и ускорения поршня не сильно различаются, но все же они есть и у двигателя с более коротким шатуном скорость и ускорения поршня больше.Отсюда можно сделать вывод, что увеличивать длину шатуна смысл есть и R/S отнюдь не миф и не байка.Но увеличение шатуна ведет к увеличению его массы и изменению развесовки, что в свою очередь увеличивает растяжение шатуна при высоких оборотах, соответственно, увеличивать шатун есть смысл до того момента, пока сила растяжения шатуна на желаемых нами оборотах не превзойдет силу его инерции, но это уже совсем отдельный расчет и для каждого двигателя он будет свой.Спасибо за внимание.В R/S сила, друзья
Изменение длины шатуна и радиуса кривошипа
В разное время было предложено большое количество конструкций шатунов с изменяемой длиной. Большая часть из них основывалась на тех же решениях, что применялись для изменения высоты поршней. Тело шатуна изготавливалось телескопическим, его длина изменялась с помощью механических или гидравлических устройств. Таким конструкциям свойственны те же недостатки, что и телескопическим поршням. Более того, надежность конструкции оказывалась еще ниже из-за того, что шатун, в отличие от поршня, подвержен большим изгибающим нагрузкам. В нескольких патентах предлагалось изменять длину шатуна путем размещения эксцентриковых элементов в верхней или нижней головках. Практическая реализация этих способов оказалась настолько сложной, что они так и остались чистыми идеями.
Применение эксцентрикового механизма также рассматривалось в качестве средства для изменения радиуса кривошипа. В этом направлении дальше всех продвинулась голландская инжиниринговая фирма Gomecsys. В предложенной ею конструкции вокруг шатунной шейки размещается подвижная эксцентриковая втулка с зубчатым венцом. Ее угловое положение изменяется за счет поворота ответной зубчатой шестерни большого диаметра с внутренним зацеплением. По такому принципу построены и исследуются 2- и 4-цилиндровый моторы – прототипы GoEngine. Разработанный механизм одновременно обслуживают два цилиндра. Поэтому он подходит только для двигателей с определенной схемой – четным числом цилиндров, из которых два соседние работают синхронно. В других случаях количество зубчатых пар, масса и габариты двигателя возрастают чрезмерно. Одно это уже значительно сужает возможности его практического применения.

Что такое радиус
И действительно:
Радиус – это отрезок, который начинается в центре окружности и заканчивается в любой точке ее поверхности. В то же время так называется и длина этого отрезка.
Само слово РАДИУС имеет латинские корни. Оно произошло от «radius», что можно перевести как «луч» или «спица колеса». Впервые этот математический термин ввел французский ученый П.Ромус. Было это в 1569 году.
Но потребовалось чуть более ста лет, чтобы слово РАДИУС прижилось и стало общепринятым.
Кстати, есть еще несколько значений слова РАДИУС:
- Размер охвата чего-нибудь или сфера распространения. Например, говорят «Огонь уничтожил все в радиусе 10 километров» или «ОН показал на карте радиус действия артиллерии»;
- В анатомии этим словом обозначают Лучевую кость предплечья.
Но, конечно, нас интересует РАДИУС как математический термин. А потому и продолжим говорить именно о нем.
Выбор размеров и числа цилиндров
Выбор размеров и числа цилиндров производится на основе следующих соображений.
Диапазон возможного изменения диаметра цилиндра можно определить, используя зависимость D = f(nн) для существующих моделей двигателей. Точки на графиках соответствуют реальным двигателям, степень концентрации точек указывает предпочтительность выбора размеров цилиндра при заданной частоте вращения. Верхние границы заштрихованной области относятся к короткоходным (S/D = 0,8…0,9), а нижние — к длинноходным (S/D = 1,1…1,2) двигателям. При известных типах двигателя и частоте вращения можно определить диапазон предпочтительных диаметров цилиндра. Назначив стандартный D (в мм, округленный на 0 или 5 — для дизелей или до ближайшего четного числа — для карбюраторных двигателей), по соответствующему соотношению S/D определяют ход поршня S и ориентировочно среднюю скорость поршня.
Из исходных данных . Принимаем D=140 мм. По соотношению 1,08 определяем ход поршня S (расстояние по оси цилиндра между мёртвыми точками) и ориентировочно среднюю скорость поршня.
Среднюю скорость поршня определяем по формуле:
Следует помнить, что Сn является показателем тепловой напряжённости и динамической нагруженности деталей двигателя и существенное её повышение.
По заданным номинальной мощности , частоте вращения коленчатого вала , оценённым размером цилиндра определяем их число .
Число цилиндров в свою очередь определяется уровнем форсирования двигателя по мощности, т. е. литровой мощностью.
Для определения литровой мощности целесообразно использовать графики Nел=f(D) (рисунок 1.2) . Согласно графику пределы литровой мощности находятся в интервале .
Устанавливаем цилиндровую мощность:
Рабочий объём цилиндра, это объём цилиндра, освобождаемый поршнем при перемещении от в.м.т. к н.м.т.
Значение D и S — принимаем в дм.
Требуемое число цилиндров определяем по формуле:
Полученное значение округляем до ближайшего целого числа, однако желательно исключить значения . Принимаем .
Необходимо уточнить значение литровой мощности по формуле: