Максимальная кинетическая энергия груза на пружине
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.
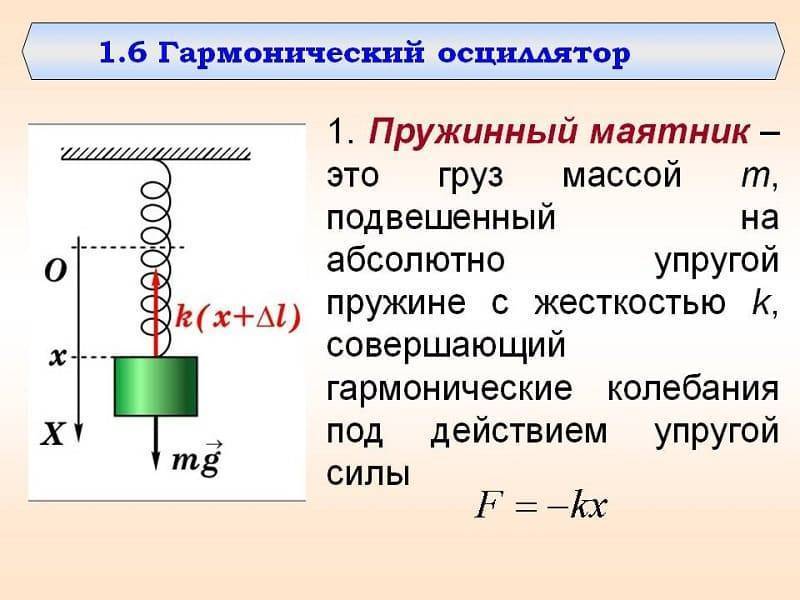
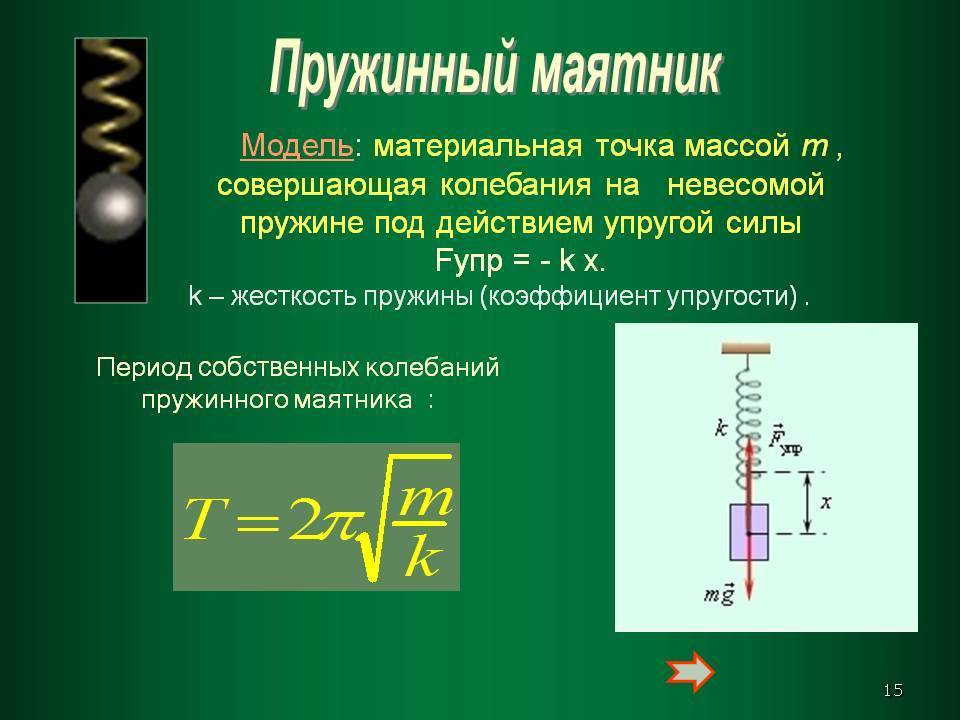
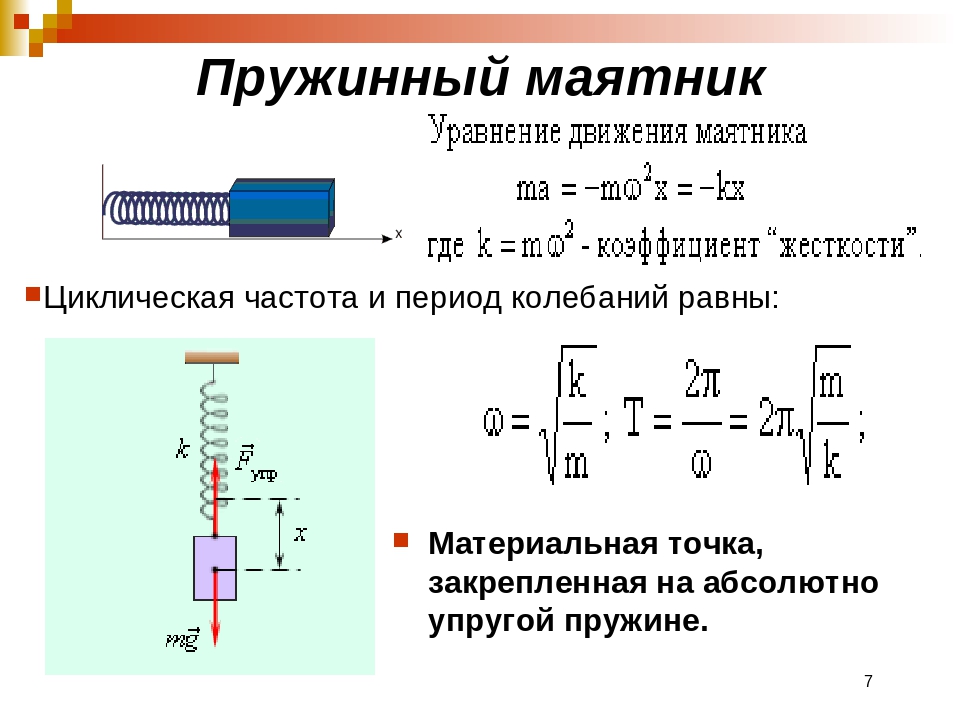
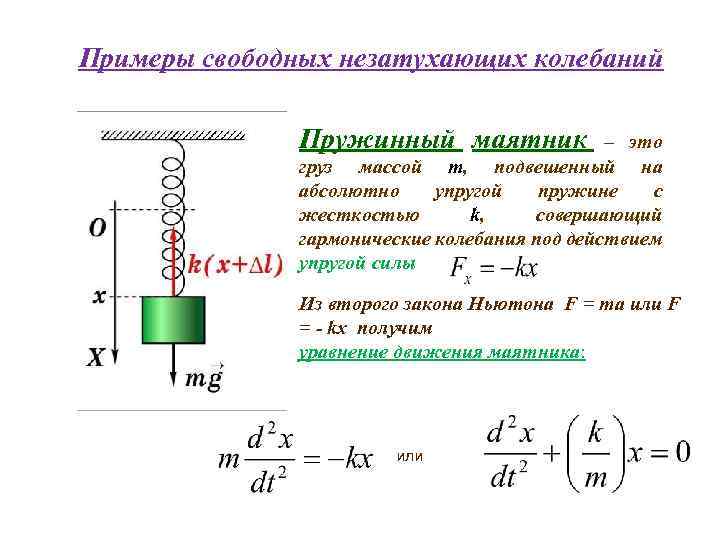
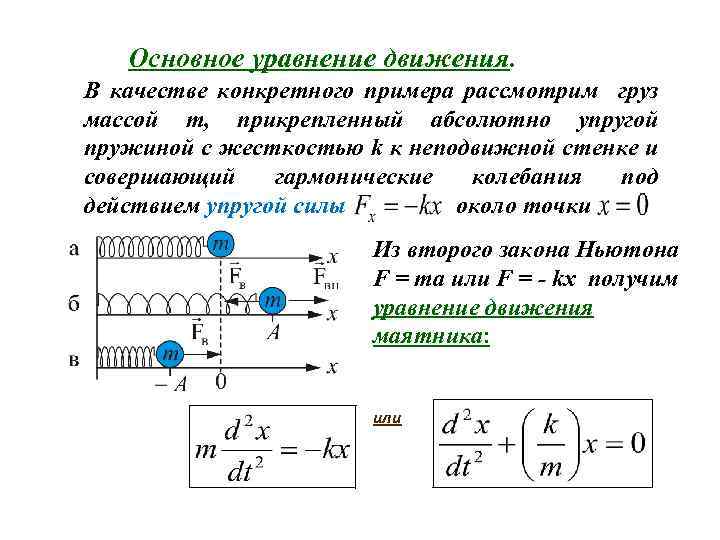
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:
В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:
Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .
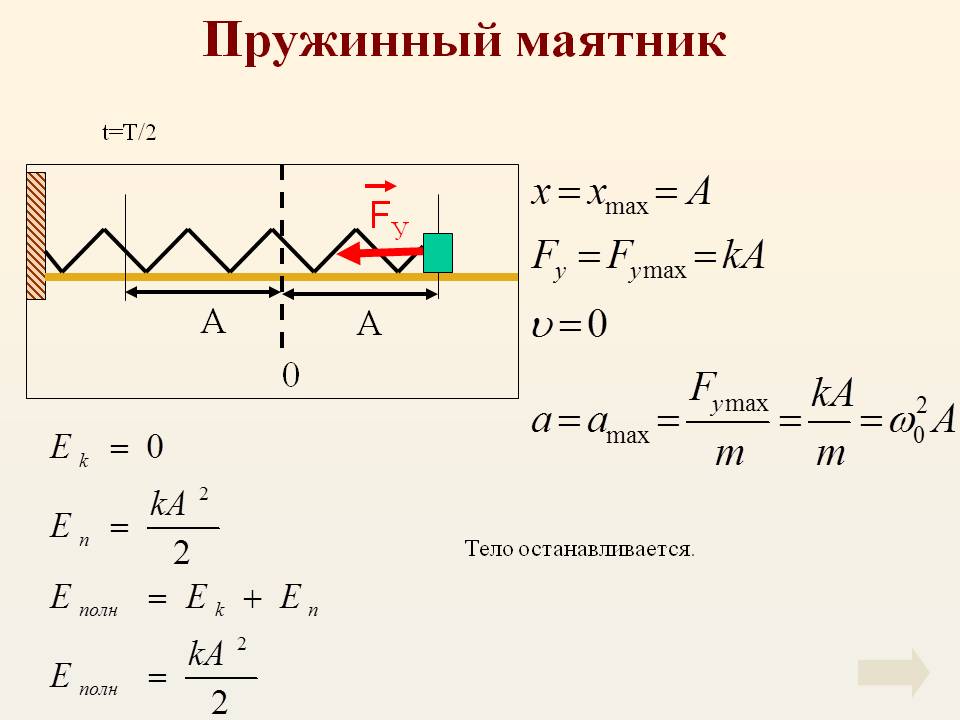
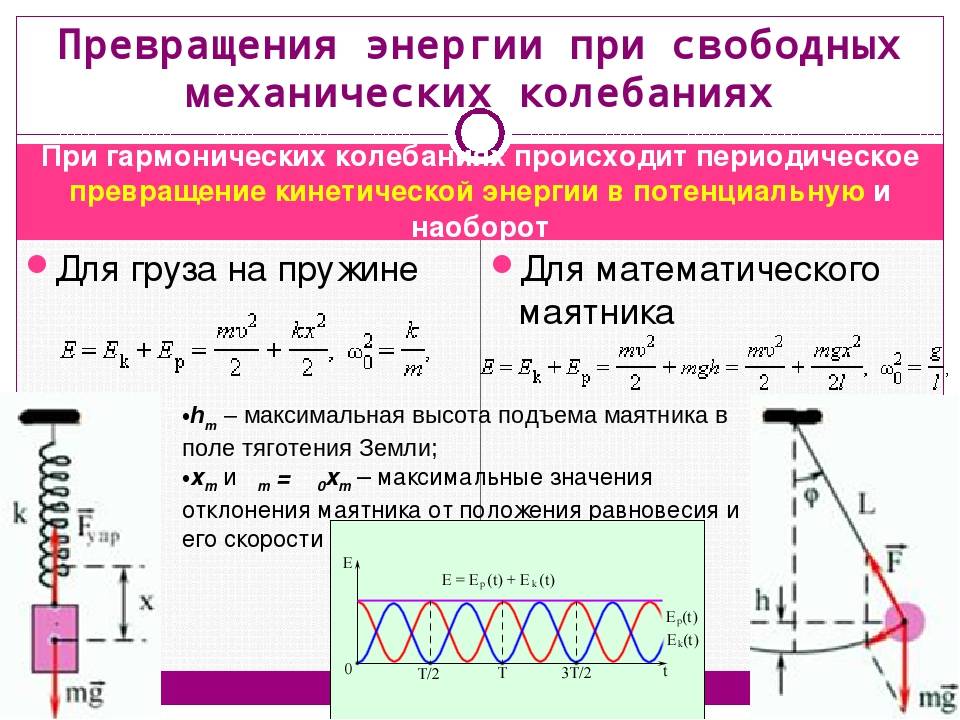
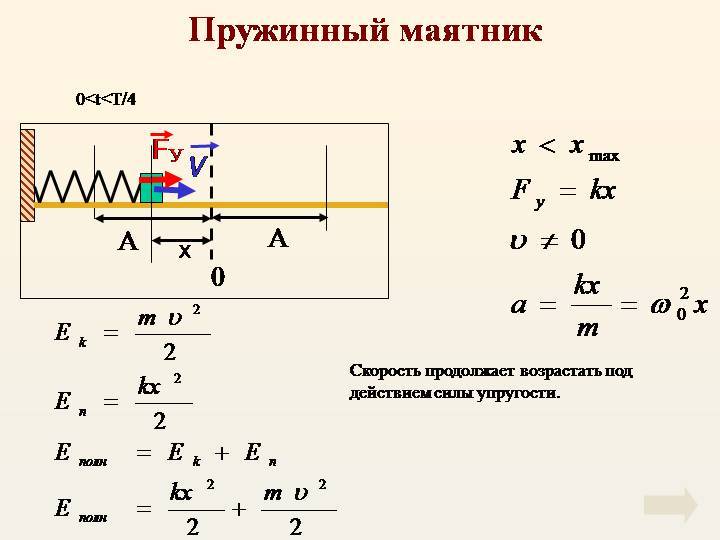
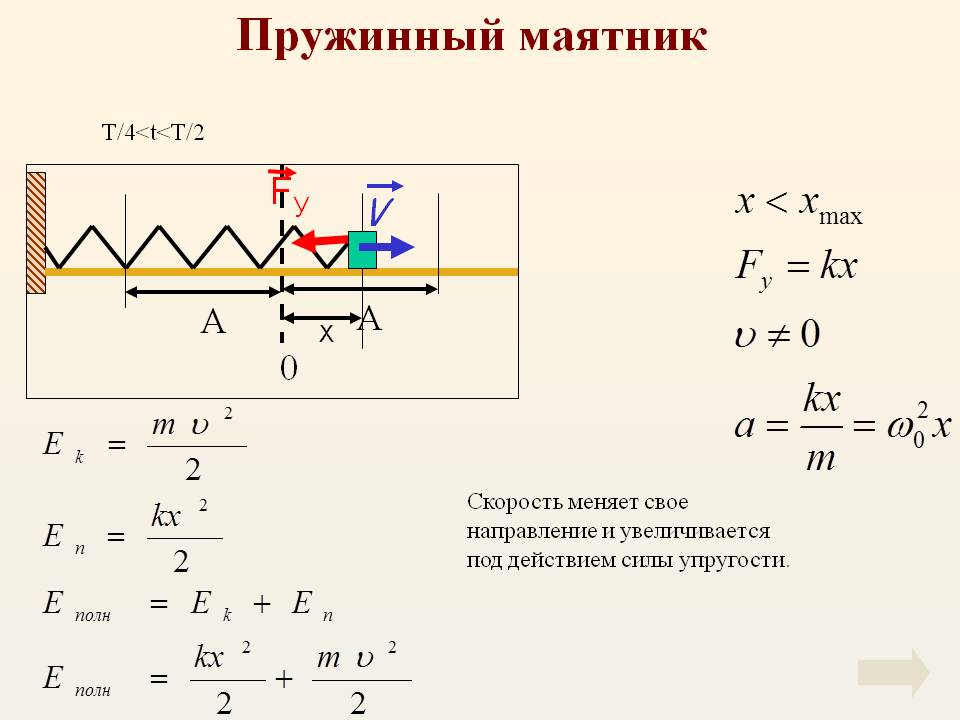
При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины.
Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.
Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.
Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.
Для груза на пружине:
Запуск колебательного движения тела осуществляется с помощью кнопки Старт . Остановить процесс в любой момент времени позволяет кнопка Стоп .
Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени
Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия
Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.
Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
1) амплитуда колебаний скорости
2) циклическая частота колебаний
3) максимальная кинетическая энергия груза
4) период колебаний
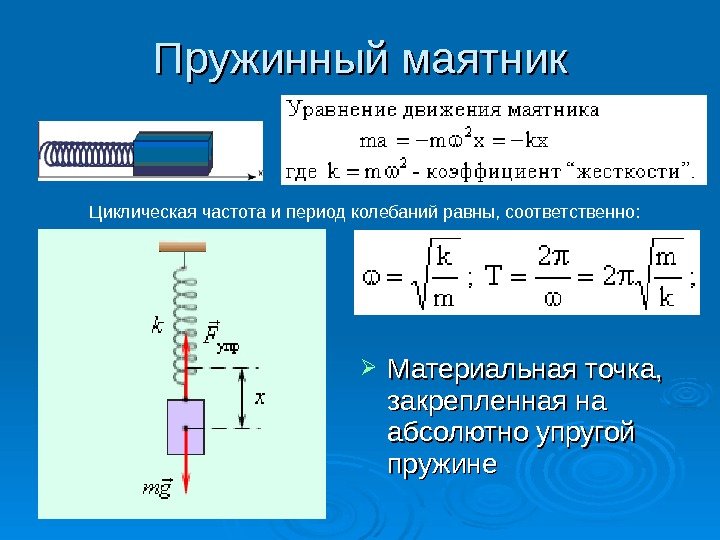
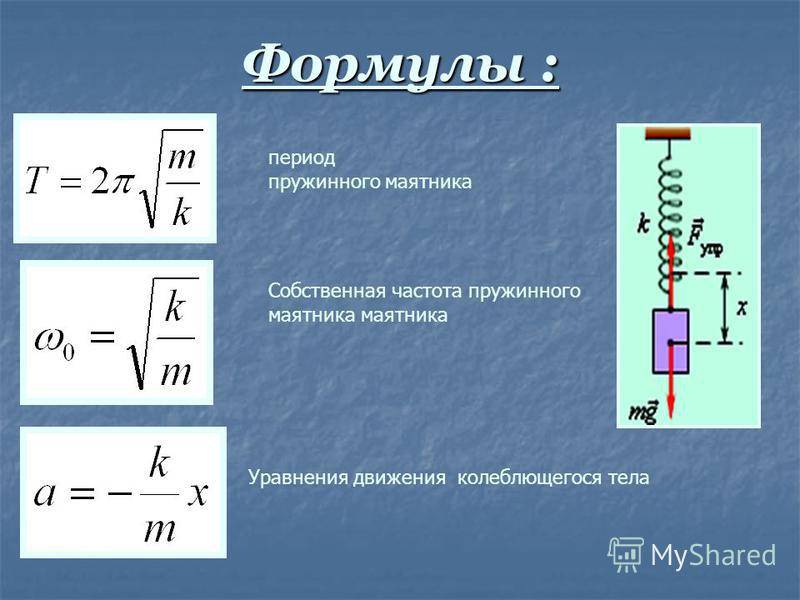
А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле
Б) Для пружинного маятника известны формулы кинетической энергии
Пружинный маятник, состоящий из груза и лёгкой пружины, совершает колебания. В момент, когда груз находится в крайнем положении, его немного подталкивают вдоль оси пружины в направлении от положения
равновесия. Как в результате этого изменяются максимальная кинетическая энергия груза маятника и частота его колебаний?
Для каждой величины определите соответствующий характер изменения:
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Максимальная кинетическая энергия груза маятника | Частота колебаний маятника |
Груз подтолкнули от положения равновесия, откуда следует, что амплитуда колебаний груза увеличится. При этом увеличится также и максимальная потенциальная энергия пружины. По закону сохранения энергии, это приведет к увеличению максимальной кинетической энергии груза маятника.
Период и частота пружинного маятника зависят только от массы груза и жесткости пружины. Таким образом, при увеличении амплитуды колебаний груза, частота колебаний маятника не изменится.
Уравнение гармонических колебаний.
Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство: . (4)
Теперь дифференцируем полученное равенство (4):
. (5)
Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :
. (6)
Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:
. (7)
C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре). Так вот, можно доказать, что:
-решением уравнения (7) является всякая функция вида (1) с произвольными ;
-никакая другая функция решением данного уравнения не является.
Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только их. Две константы определяются из начальных условий — по начальным значениям координаты и скорости.
Постигаем закон Гука
Все объекты природы могут деформироваться, т.е. менять свою форму или объем, под действием приложенной силы. Если такие деформации (т.е. изменения) исчезают после прекращения действия приложенной силы, то они называются упругими. Упругость играет важную роль в технике. Упругие пружины используются для гашения удара при посадке космического корабля на поверхность планеты. Свернутые в спираль упругие пластины применяются в заводных механизмах часов. Даже в мышеловке используется упругая деформация пружины.
Еще в XVII-M веке английский физик Роберт Гук, изучая упругие свойства разных материалов, вывел закон, названный его именем. Согласно закону Гука, для упругого деформирования материала требуется приложить силу, величина которой прямо пропорциональна его деформации. Например, чтобы растянуть пружину на величину \( x \), потребуется приложить внешнюю силу \( F_{вн} \), которая равна:
где \( k \) — это коэффициент пропорциональности.
Точнее говоря, вектор деформации \( \mathbf{x} \) всегда направлен противоположно силе сопротивления пружины (или силе упругости) \( \mathbf{F} \), а потому в векторную формулировку закона Гука обычно входит знак “минус”:
Растягиваем и сжимаем пружины
В реальном мире, помимо упругих деформаций, имеются еще и пластические деформации. Так называют деформации, которые остаются в объекте, хотя бы частично, даже после прекращения действия внешних сил. Если сила не превосходит некоторой известной величины, которая называется пределом упругости, то возникающая деформация будет пластической. Предел упругости имеет разные значения для разных материалов. Если деформируемый объект, например пружина, испытывает только упругие деформации, то его называют идеально упругим, например, идеально упругой пружиной. Коэффициент пропорциональности \( k \) в законе Гука \( F=kx \) называется коэффициентом упругости объекта, который зависит от материала объекта, его размеров и измеряется в Н/м.
Допустим, вам нужно спроектировать подвеску автомобиля массой 1000 кг, состоящую из 4 пружин, которые могут идеально упруго деформироваться на расстояние 0,5 м. Каким коэффициентом упругости должна обладать пружина, чтобы выдержать вес автомобиля?
Вес автомобиля равен \( mg \), где \( g \) — это ускорение свободного падения под действием силы гравитационного притяжения. Это значит, что на каждую пружину приходится вчетверо меньшая нагрузка \( mg/4 \).
Определим упругую деформацию пружины под действием этой нагрузки по формуле закона Гука:
т.е. коэффициент упругости равен:
Подставляя значения, получим:
Итак, чтобы выдержать вес автомобиля, потребуется пружина с коэффициентом упругости равным 4,9·103 Н/м. Не забудьте, что каждый элемент подвески автомобиля должен обладать определенным запасом прочности, чтобы выдерживать непредсказуемые превышения нагрузки, например на ухабах. Однако эта задача выходит за рамки данного курса.
Изучаем особенности закона Гука
Как уже упоминалось выше, в векторную формулировку закона Гука обычно входит знак “минус”:
Таким образом, знак “минус” выражает следующую особенность упругой деформации: сила упругости всегда противоположна деформации. На рис. 12.1 схематически показаны направления силы упругости и деформации при сжатии и растяжении пружины.

Как видите, при отсутствии растяжении или сжатия нет и деформации (см. схему А на рис. 12.1). Если пружина сжимается влево, то сила упругости направлена вправо (см. схему Б на рис. 12.1), а если пружина растягивается вправо, то сила упругости направлена влево (см. схему В на рис. 12.1).
Энергия кинетическая: формула и определение
Иногда значение механической работы можно рассматривать без употребления понятий силы и перемещения, акцентировав внимание на том, что работа характеризует изменение энергии тела. Все, что нам может потребоваться, — это масса некоего тела и его начальная и конечная скорости, что приведет нас к кинетической энергии
Кинетическая энергия (КЭ) — это энергия, принадлежащая телу вследствие собственного движения
Кинетическая энергия (КЭ) — это энергия, принадлежащая телу вследствие собственного движения.
Кинетическую энергию имеет ветер, ее используют для придания движения ветряным двигателям. Движимые массы воздуха оказывают давление на наклонные плоскости крыльев ветряных двигателей и заставляют их оборачиваться. Вращательное движение при помощи систем передач передается механизмам, выполняющим определенную работу. Движимая вода, оборачивающая турбины электростанции, теряет часть своей КЭ, выполняя работу. Летящий высоко в небе самолет, помимо ПЭ, имеет КЭ. Если тело пребывает в состоянии покоя, то есть его скорость относительно Земли равна нулю, то и его КЭ относительно Земли равна нулю. Экспериментально установлено, что чем больше масса тела и скорость, с которой оно движется, тем больше его КЭ. Формула кинетической энергии поступательного движения в математическом выражении следующая:
Где К — кинетическая энергия, m — масса тела, v — скорость.
Это интересно: Мангал из газового баллона своими руками — чертежи, фото, как сделать
Гармонические колебания.
Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение . Основная задача механики в данном случае состоит в нахождении функции , дающей координату тела в любой момент времени.
Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них – синус и косинус – являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.
Читать также: Каким сверлом сверлить плитку керамическую
Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.
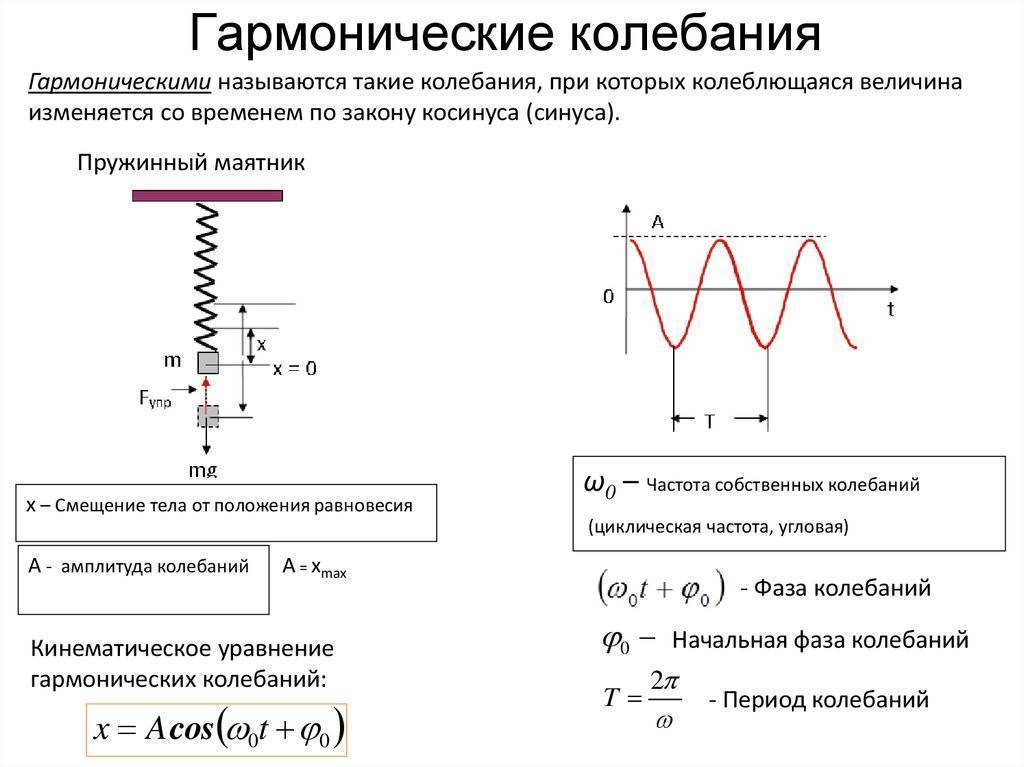
Гармонические колебания – это колебания, при которых координата зависит от времени по гармоническому закону:
Выясним смысл входящих в эту формулу величин.
Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому – амплитуда колебаний.
Аргумент косинуса называется фазой колебаний. Величина , равная значению фазы при , называется начальной фазой. Начальная фаза отвечает начальной координате тела: .
Величина называется циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное радиан: , откуда
Измеряется циклическая частота в рад/с (радиан в секунду).
В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1) :
График функции (1) , выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1 .
|
| Рис. 1. График гармонических колебаний |
Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.
Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить . Мы получаем закон косинуса:
График гармонических колебаний в этом случае представлен на рис. 2 .
|
| Рис. 2. Закон косинуса |
Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить . Получаем закон синуса:
График колебаний представлен на рис. 3 .
|
| Рис. 3. Закон синуса |
Звук
Звук – это колебания упругой среды, воспринимаемые органом слуха.
Условия, необходимые для возникновения и ощущения звука:
- наличие источника звука;
- наличие упругой среды между источником и приемником звука;
- наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
- мощность звука должна быть достаточной для восприятия.
Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.
Классификация звуковых волн:
- инфразвук (\( \nu \) < 16 Гц);
- звуковой диапазон (16 Гц < \( \nu \) < 20 000 Гц);
- ультразвук (\( \nu \) > 20 000 Гц).
Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.
Скорость звука зависит
от упругих свойств среды:
в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
от температуры среды:
в воздухе при температуре 0°С – 331 м/с, в воздухе при температуре +15°С – 340 м/с.
Характеристики звуковой волны
- Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
- Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
- Тембр – это окраска звука.
Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.Шум – хаотическая смесь тонов.
Слайды и текст этой презентации

Исследование зависимости периода колебаний пружинного маятника от массы груза, жёсткости пружины, амплитуды колебаний и температуры воздуха.
Работа учащихся 9 класса МОУ «Старовыслинская ООШ»Шингалова Радия и Надукова Дениса
2011г. Учитель: Потапов Н.А.

Цель нашей работы:
Исследовать зависимость периода колебаний пружинного маятника от массы груза, жёсткости пружины, амплитуды колебаний и температуры воздуха.

Введение.
В настоящее время в технике и быту используются различные виды пружины. Твердые тела и материалы, которыми располагает человечество, во многом определяет уровень его технического развития. Изучая свойства твердых тел, мы заинтересовались упругими свойствами пружины и решили исследовать их.

Подготовка к эксперименту
Для проведения экспериментов подобрали следующее оборудование: штатив с 2-мя лапками, пружина №1 (к1=6,4 Н/м), пружина №2 (к2=21,6Н/м), набор грузов массой по 100г, линейка, секундомер, динамометр.

ПЕРИОД КОЛЕБАНИЯ
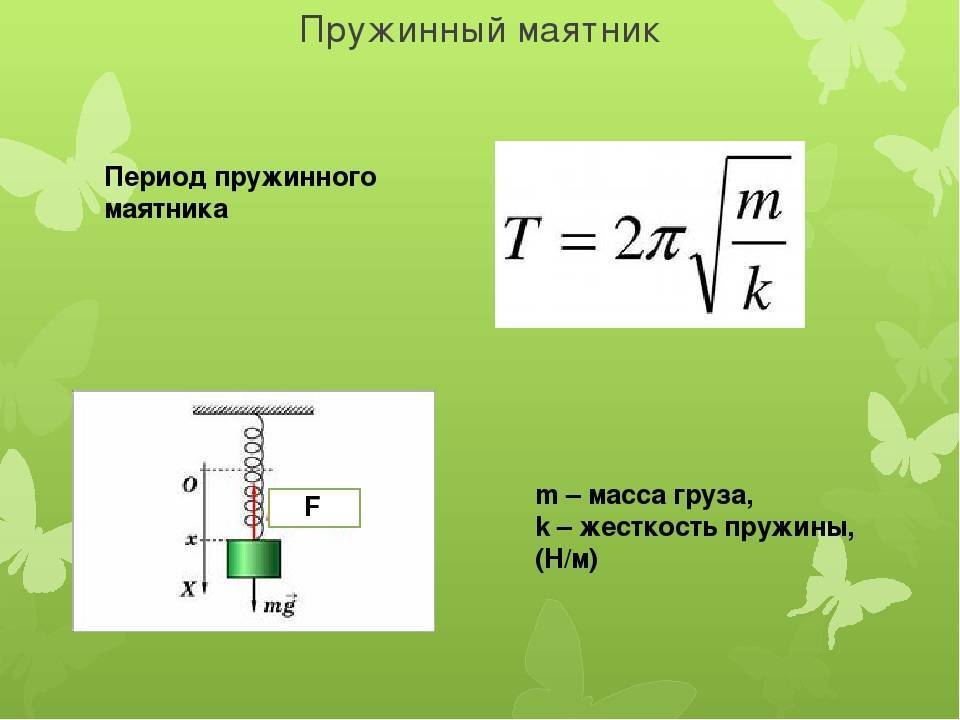
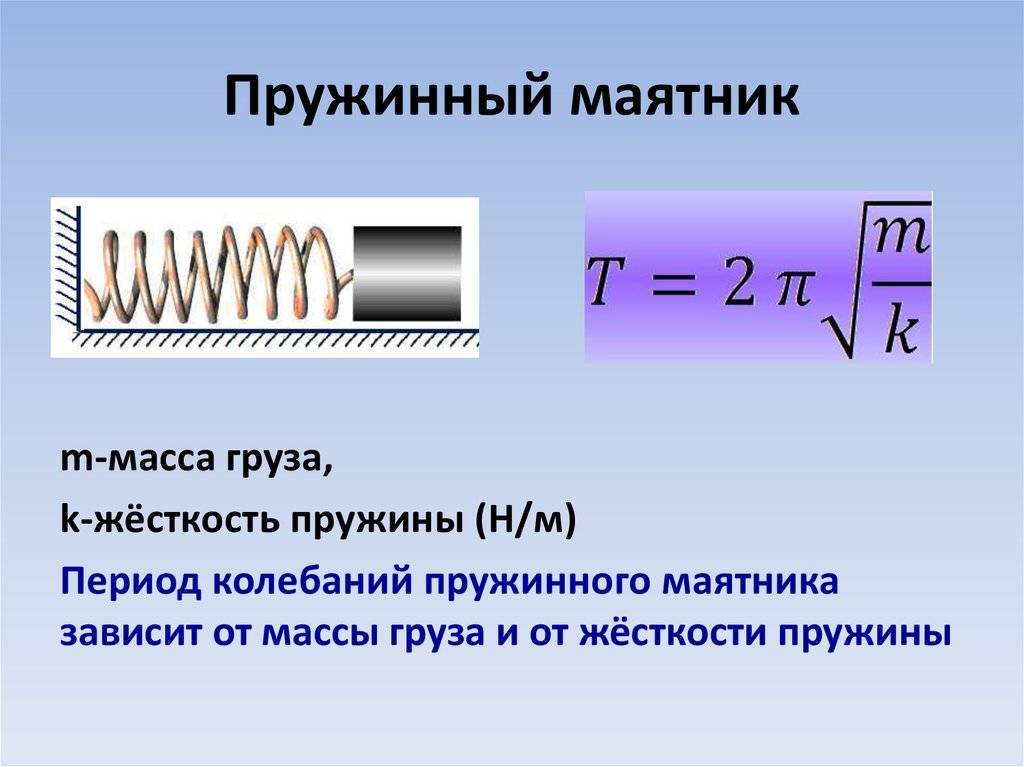
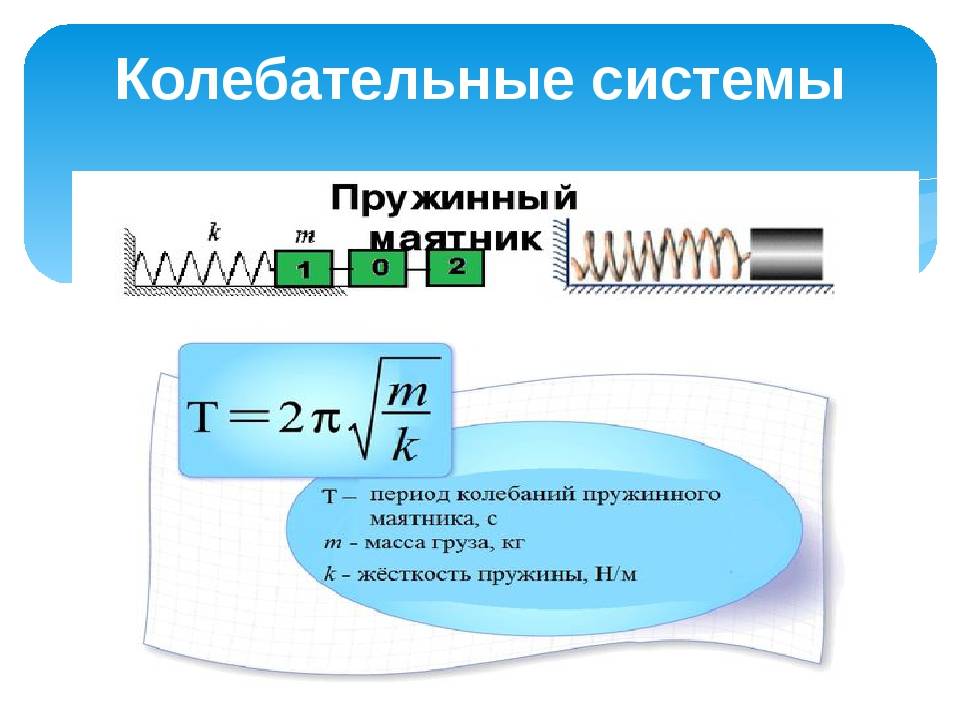
Одной из важных характеристик колебательного движения является период колебания – интервал времени, в течение которого происходит одно полное колебание. Связь периода колебаний пружинного маятника от массы груза и жёсткости пружины известна:

План проведения эксперимента:
Приготовить приборы и оборудования.Исследовать зависимость периода колебаний пружинного маятника от массы груза, жёсткости пружины, амплитуды и температуры воздуха. Заполнение таблиц измерений.Вычерчивание графиков зависимостей.Анализ графиков зависимостей периода от разных параметров. Обобщение результатов.

Эксперимент 1 Исследование зависимости периода колебаний пружинного маятника от массы груза.
Подвесим к штативу пружину №1. Возьмем гирю массой 100г и прикрепим к пружине. С помощью секундомера определим время 10 колебаний пружинного маятника. Повторим эксперимент с гирями 200г и 300г. Определим по формуле период колебаний:
Результаты измерений и вычислений запишем в таблицу 1:

график зависимости периода колебаний от массы груза
ВЫВОД: Период колебания пружинного маятника пропорционален корню квадратному из массы тела: Т ~

Эксперимент 2 Исследование зависимости периода колебаний пружинного маятника от жёсткости пружины
Подвесим к штативу пружину №2. Возьмем гирю массой 100г и прикрепим к пружине. С помощью секундомера определим время 10 колебаний пружинного маятника. Повторим эксперимент с гирями 200г и 300г. Определим по формуле период колебаний:
Результаты измерений и вычислений запишем в таблицу 2:

график зависимости периода колебаний от жёсткости пружины
ВЫВОД: Период колебаний пружинного маятника зависит обратно пропорционально жесткости пружины:

Эксперимент 3 Исследование зависимости периода колебаний пружинного маятника от амплитуды колебаний
Результаты измерений и вычислений запишем в таблицу 3:
Не изменяя массы груза, жесткости пружины, установим зависимость периода колебаний от амплитуды. Повторим эксперимент №1 при разных амплитудах колебаний.

график зависимости периода колебаний от амплитуды колебаний
ВЫВОД: Эксперимент подтверждает, что период свободных колебаний пружинного маятника не зависит от амплитуды колебаний, а полностью определяется собственными характеристиками колебательной системы (жесткостью k и массой груза m).

Эксперимент 4 Исследование зависимости периода колебаний пружинного маятника от температуры.
Для исследования зависимости периода колебаний пружинного маятника от температуры повторили эксперимент №1 во дворе школы при другой температуре ( t= -20 0С ).
ВЫВОД: Период колебания пружинного маятника не зависит от температуры.

Обобщение
В результате экспериментов мы выяснили, что период колебаний пружинного маятника зависит от массы тела, жёсткости пружины и не зависит от амплитуды колебаний и температуры.

Литература:
Учебник по физике для 9 класса средней школы Н.М. Шахмаева, С.Н. Шахмаева, Д.Ш. Шодиева,-М. Просвещение.1990г. Кикоин И.К., Кикоин А.К. Физика. Учебник для 9кл.-М. Просвещение, 1990г.Громов С.В. , Родина Н.А.. Физика. Учеб. Для 8кл.-М. Просвещение. 2000г.Сеть Интернет.
Типы и виды пружин
Как ранее было отмечено, изготавливаются различные виды пружин, все они обладают своими определенными особенностями, которые стоит учитывать. Классификация проводится по конструктивным признакам. Выделяют следующие типы пружин:
Винтовые. Эта разновидность встречается в различных механизмах, устанавливается практически везде, к примеру, в автомобилях. При этом выделяют следующие типы автомобильных пружин: цилиндрические и конические, а также с переменным диаметром. Следует учитывать, что рассматриваемое изделие представлено витками с одинаковым и различным диаметром. Довольно распространенный признак применения заключается в установке пружинных амортизаторов, которые являются важным элементом конструкции автомобиля. В некоторых случаях проводится установка пружины с переменным шагом витков. Торсионные. Во многом этот вариант исполнения напоминает предыдущий, но при этом работает на кручение и изгиб. Подобная форма пружины позволяет устанавливать ее в качестве основного элемента подвески. Этот же механизм устанавливается для открытия и закрытия дверей, обеспечения функциональности противовесов. Спиральные. Этот вариант исполнения напоминает плоский вид пружины, который закручивается по спирали в виде ленты. Применяется устройство в качестве элемента для накопления кинетической энергии, освобождение которой происходит в определенных случаях. Примером можно назвать настенные или наручные часы, а также другие подобные механизмы. Тарельчатые
Рассматривая классификацию пружин следует уделить внимание тарельчатому варианту исполнения. Этот вариант исполнения не напоминает стандартный вид пружины, так как состоит из нескольких последовательных дисков, соединенных между собой. Основным преимуществом этого варианта исполнения можно назвать слабую степень деформации даже в случае оказания высокой нагрузки
Основным преимуществом этого варианта исполнения можно назвать слабую степень деформации даже в случае оказания высокой нагрузки
Зачастую устанавливается в случае изготовления предохранительных клапанов. Волновые. Этот вид представлен изогнутой по синусоиде металлической лентой, которая плавно накручивается по спирали. Достоинством можно назвать относительно небольшие размеры, из-за высокой точности применяются при создании опорных узлов, подшипников и арматуры, которая перекрывает поток при необходимости. Газовые. Этот вариант исполнения отводится в особую категорию, так как при изготовлении не применяется проволока, а газ вместе с поршнем. Высокая стоимость определена сложностью конструкции, однако она может гасить вибрации и нагрузки с высокой эффективностью.
Основным преимуществом этого варианта исполнения можно назвать слабую степень деформации даже в случае оказания высокой нагрузки. Зачастую устанавливается в случае изготовления предохранительных клапанов. Волновые. Этот вид представлен изогнутой по синусоиде металлической лентой, которая плавно накручивается по спирали. Достоинством можно назвать относительно небольшие размеры, из-за высокой точности применяются при создании опорных узлов, подшипников и арматуры, которая перекрывает поток при необходимости. Газовые. Этот вариант исполнения отводится в особую категорию, так как при изготовлении не применяется проволока, а газ вместе с поршнем. Высокая стоимость определена сложностью конструкции, однако она может гасить вибрации и нагрузки с высокой эффективностью.
Рассматривая все о пружинах следует уделить внимание также классификации по характеру нагрузки. По этому признаку выделяют следующие варианты исполнения:
- Изгиб. Подобный вид пружины при воздействии силы несущественно меняет свои размеры. Распространены торсионные пакеты, а также тарельчатые виды пружины.
- Пружина кручения. Этот вариант характеризуется небольшими размерами, устанавливаются при изготовлении прищепок.
- Сжатие и растяжение. Этот тип пружины весьма распространен, при приложении требуемого усилия происходит изменение линейных размеров. Сегодня он встречается в самых различных механизмах. Сжатие и растяжение применяется при создании промышленного и бытового оборудования.
Приведенная выше информация указывает на то, что есть просто огромное количество различных видов пружин, которые применяются в качестве основных элементов различных механизмов.