Линейчатые поверхности

7.6. Сферическая поверхность

Сферическая поверхность – поверхность, образованная вращением окружности вокруг отрезка, являющегося её диаметром.

Шаром называется тело, ограниченное сферической поверхностью.

Экватор – это окружность, которая получается пересечением сферы горизонтальной плоскостью, проходящей через ее центр (Рисунок 7.10).

Меридиан – это окружность, которая получается пересечением сферы плоскостью, перпендикулярной плоскости экватора и проходящей через центр сферы.

Параллелями называются окружности, которые получаются пересечением сферы плоскостями, параллельными плоскости экватора.

Рисунок 7.10 – Проецирование сферической поверхности

Прямоугольная проекция шара (сферы) на любую плоскость – есть окружность, которую часто называют очерковой.

Рисунок 7.11 – Эпюр сферы и принадлежащих ей точек

1.6. ВЗАИМНОЕ ПОЛОЖЕНИ ЛИНИИ И ПОВЕРХНОСТИ

Различают четыре возможных варианта взаимного положения линии и поверхности:

–  линия и поверхность не имеют общих точек;

–  линия касается поверхности;

–  линия принадлежит поверхности;

–  линия пересекает поверхность.

Первый вариант не рассматривают, т. к. он не имеет практического применения. Способ построения линий, принадлежащих поверхности основан на использовании ее каркаса и рассмотрен на примерах разработки комплексных чертежей поверхностей (рис. 1.54 и 1.57).

1.6.1. Построение касательной к поверхности

Задачу на построение касательной к поверхности сводят к построению касательной к линии, которая принадлежит поверхности и проходит через заданную точку.

Из за большого объема этот материал размещен на нескольких страницах:1 2 3 4 5 6 7 8 9 10 11 12 13 14

7.12. Пересечение конуса плоскостью

Рассмотрим пять возможных вариантов расположения плоскости относительно поверхности прямого кругового конуса. Пусть плоскость сечения перпендикулярна плоскости проекций π₂ (Рисунок 7.16).

Рисунок 7.16

1. Если плоскость проходит через вершину (1) – в сечении две образующие и прямая пересечения с плоскостью основания.
2. Если плоскость перпендикулярна оси вращения конуса (2) – в сечении окружность.
3. Если плоскость не параллельна ни одной образующей (пересекает все образующие (3)) – в сечении эллипс.
4. Если плоскость параллельна одной образующей конуса – в сечении парабола (на примере – плоскость сечения (4) параллельна крайней образующей конуса).
5. Если плоскость параллельна двум образующим (пересекает обе полости конической поверхности (5)) – в сечении гипербола (рисунок 7.17).

Рисунок 7.17. Плоскость сечения параллельна двум образующим конуса

Ниже, на моделях, представлены варианты положения секущей плоскости относительно поверхности конуса, при которых получаются сечения в виде эллипса, параболы и гиперболы.

Рисунок 7.18 – Сечение конической поверхности плоскостью (а — эллипс, б — парабола, в — гипербола)

Рассмотрим пример построения сечения конической поверхности плоскостью.

Рисунок 7.19 – Построение пересечения конической поверхности плоскостью

Пусть задана секущая проецирующая плоскость σ⊥π₂ (Рисунок 7.19). Если продлить коническую поверхность и проекцию плоскости, то видно, что плоскость пересекает вторую ветвь конической поверхности, следовательно, в сечении получится гипербола.

1. Построим характерные точки. Это точки, лежащие на крайних образующих и на окружности основания конуса (1, 2, 3). Их проекции строятся по линиям проекционной связи.
2. Для построения промежуточных точек, воспользуемся методом вспомогательных секущих плоскостей. Введём плоскость α⊥π₂ и перпендикулярно оси вращения, что даст в сечении окружность радиусом r. Строим эту окружность на π₁. Плоскость α пересекает и заданную плоскость сечения по прямой, проекции которой на π₁ и π₃ совпадают с линиями проекционной связи.
3. На пересечении этих двух сечений на плоскости проекций π₁ строим точки 4, 5. Профильные проекции этих точек строим по линии проекционной связи, откладывая расстояние от оси вращения конуса, равное Δ.
4. Аналогично строим точки 6, 7. Плавно соединим построенные точки, образуя гиперболу.
5. Обведём то, что осталось от конуса после такого среза с определением видимости. В нашем примере все проекции построенной кривой будут видимы.

На анимации ниже представлена последовательность построения пересечения конической поверхности плоскостью.

Презентация на тему: ” Линейчатые поверхности Образование поверхностей. Линейчатой поверхностью называется поверхность, образованная перемещением прямолинейной образующей по.” — Транскрипт:

1

Линейчатые поверхности Образование поверхностей

2

Линейчатой поверхностью называется поверхность, образованная перемещением прямолинейной образующей по одной или более направляющим

3

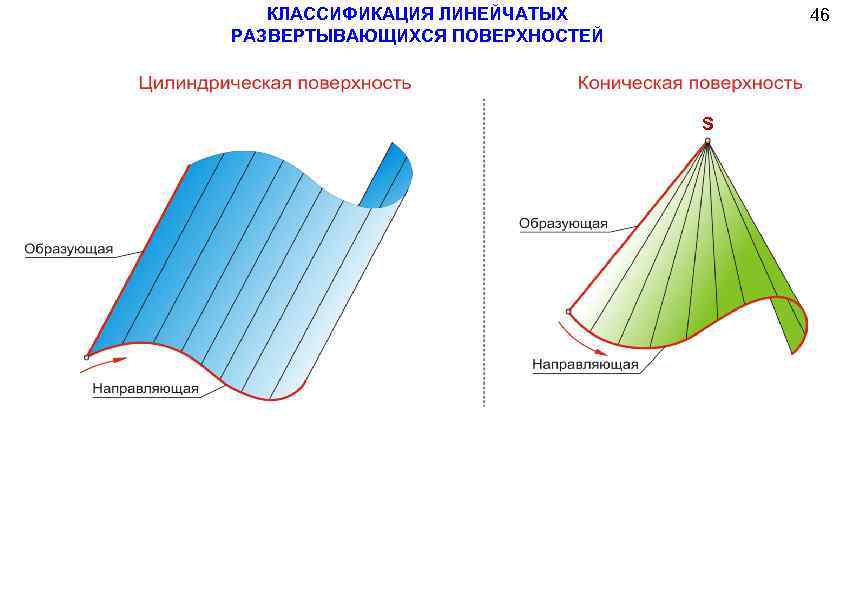
Цилиндрическая поверхность m (m; S ) S // Цилиндрическая поверхность образуется движением прямой (образующей) по некоторой кривой m параллельно самой себе или имеющей постоянное направление S

4

i m ( i, m; i ) Коническая поверхность Коническая поверхность – образуется движением прямой линии (о бразующей) по некоторой кривой линии m и имеющей неподвижную точку S S

5

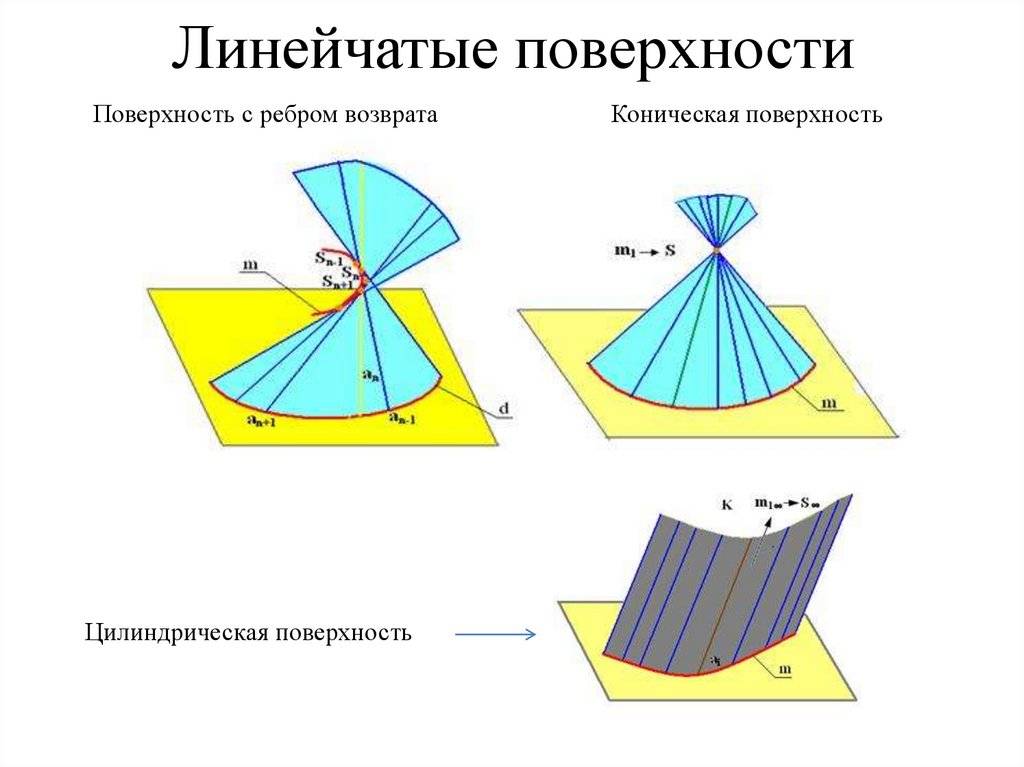
Торсовая поверхность m m – ребро возврата ( m) Торсовая поверхность образуется движением прямой, касающейся во всех своих положениях некоторой пространственной направляющей кривой m, называемой ребром возврата

6

Однополостный гиперболоид

7

Многогранные поверхности – это поверхности, образованные частями (отсеками) пересекающихся плоскостей Многогранником называется тело, ограниченное многогранной поверхностью, состоящей из плоских многоугольников Отсеки плоскостей называются гранями, а линии их пересечения – ребрами Точки пересечения ребер называются вершинами

8

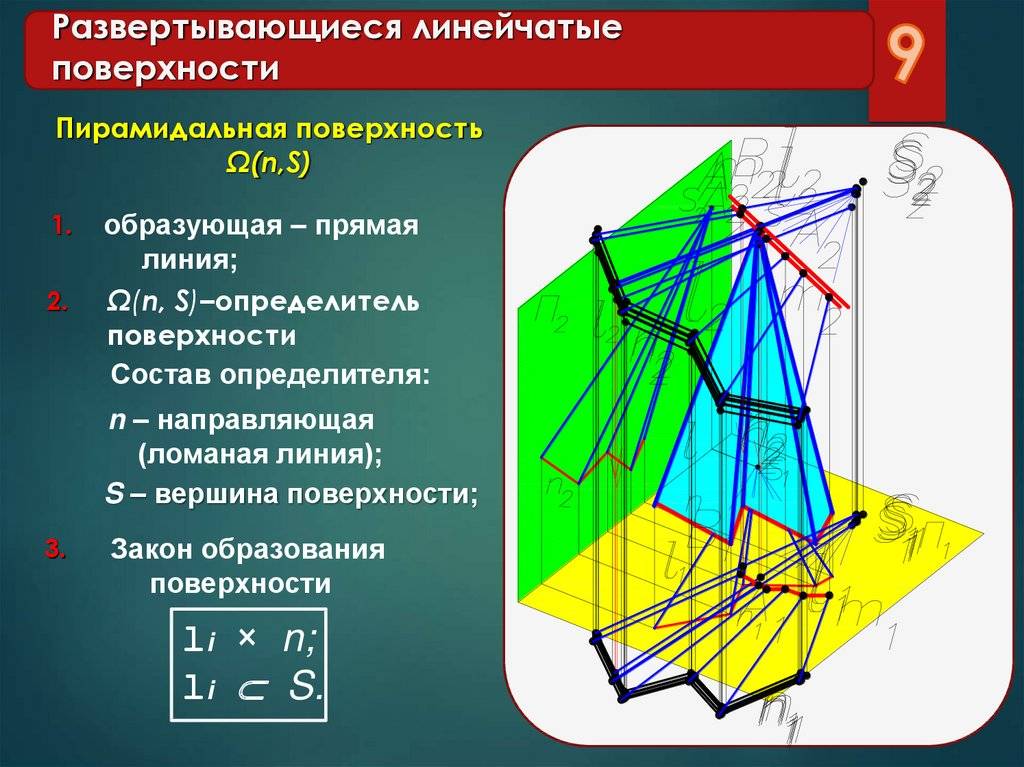
S m S m Пирамидальная поверхность S m Пирамида m – замкнутый контур Если направляющая m ломаная, а все образующие пересекаются в одной точке, такая поверхность называется пирамидальной Поверхность с замкнутой ломаной направляющей (m), общей точкой пересечения образующих ребер и граней называется пирамидой

9

Принадлежность точки поверхности

10

S А1А1 С1С1 В1В1 S2S2 X 1,2 S1S1 А2А2 С2С2 В2В2 Задача Построить недостающую проекцию точки N N2N2 N1N1

11

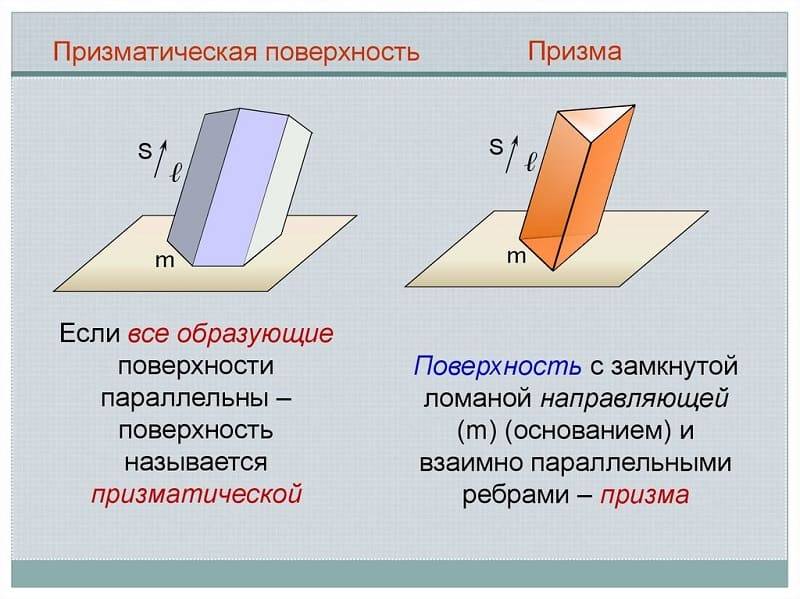
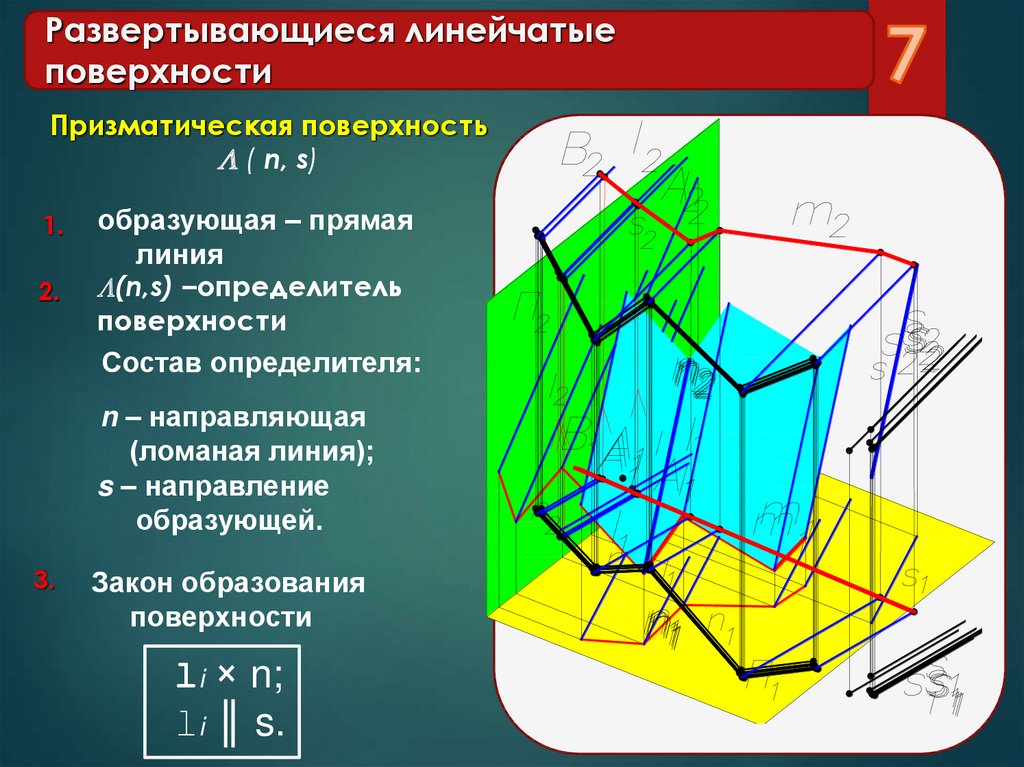
m S Призматическая поверхность m S Призма Если все образующие поверхности параллельны – поверхность называется призматической Поверхность с замкнутой ломаной направляющей (m) (основанием) и взаимно параллельными ребрами – призма

12

Проецирующая призма А В С С1С1 В1В1 А1А1 k2k2 k1k1 f1f1 g1g1 g2g2 f2f2 X 1,2 Если ребра призмы перпендикулярны основанию, гранник называется проецирующей призмой

13

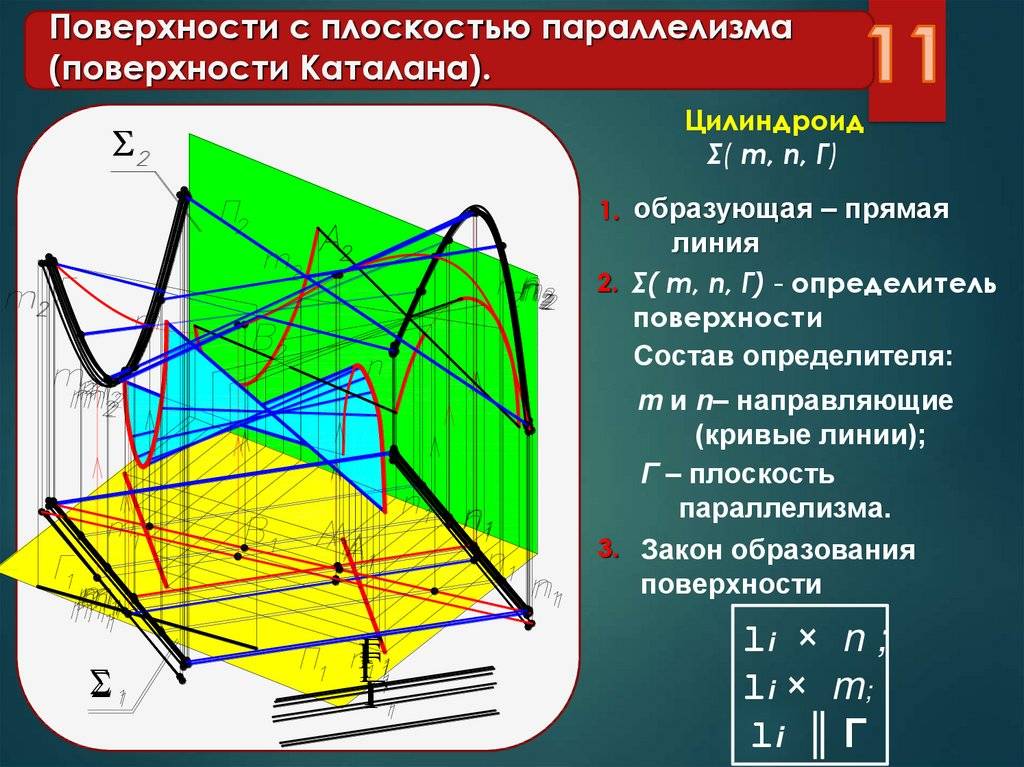
Поверхности Каталана

14

0 m1m1 n1n1 1 1 n m n1n1 m1m1 2 m2m2 n2n2 Линейчатые поверхности с двумя направляющими (поверхности Каталана) П 2 (m,n,; П 2 ); Цилиндроид

15

Поверхность с плоскостью параллелизма и двумя скрещивающимися направляющими называется гиперболическим параболоидом, или косой плоскостью Гипар

16

m2m2 n2n2 n1n1 m1m1 Задача Построить каркас и очерк гипара, заданного определителем (m, n, П 2 ) I21I2 2I22I2 3I23I2 4I24I2 5I25I2 6I26I2 7I27I2 8I28I I21I2 2I22I2 3I23I2 4I24I2 5I25I2 6I26I2 7I27I2 8I28I2 // парабола ll 1 n m ; 1 1 ll П 2 Определить видимость очерковых линий

17

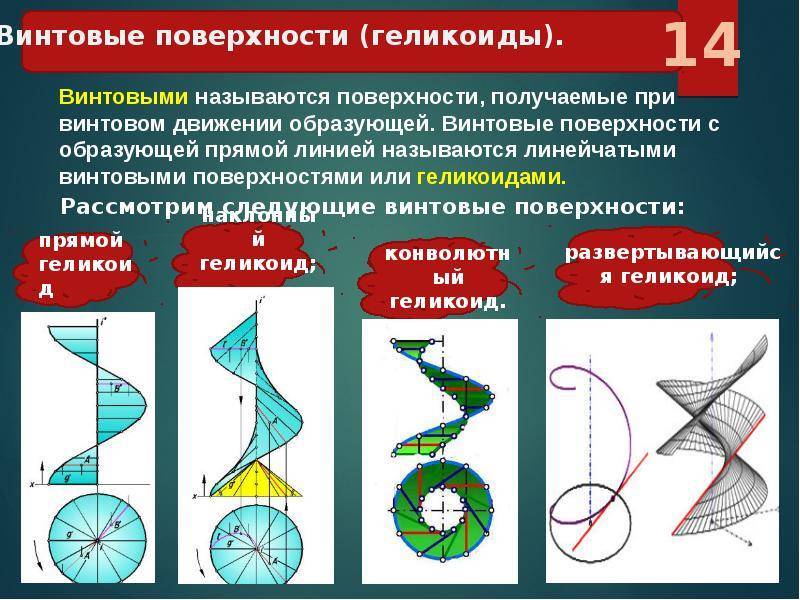
Винтовой поверхностью называют поверхность, образованную винтовым движением образующей Винтовым движением называют движение, при котором каждая точка А образующей вращается вокруг неподвижной оси i и одновременно перемещается поступательно вдоль этой оси Винтовая поверхность

18

n2n2 n1n1 гелиса А1А1 В1В1 ί1ί1 ί2ί2 Задача Построить каркас и очерк прямого геликоида А2А2 В2В (Прямой винтовой коноид) (n, i)

19

Задача А2А2 А1А1 В1В1 В2В2 i2i2 i1i1 Построить очерк однополостного гиперболоида вращения Однополостный гиперболоид вращения

Линейчатые поверхности в архитектуре [ править ]

Поверхности с двойной линией – это вдохновение для изогнутых гиперболоидных структур, которые можно построить с помощью решетки из прямых элементов, а именно:

• Гиперболические параболоиды, например, двускатные крыши .
• Гиперболоиды одного листа, такие как градирни и некоторые урны для мусора .

В ракетном двигателе RM-81 Agena использовались прямые охлаждающие каналы , расположенные на линейчатой ​​поверхности и образующие горловину сопловой секции.

• Охлаждение гиперболические башни на электростанции Didcot , Великобритания; поверхность может быть двояко линейчатой.

• Дважды управляемая водонапорная башня с тороидальным резервуаром, работы Яна Богуславского в Цехануве , Польша.

• Гиперболоидная башня порта Кобе , Кобе , Япония, с двойной линией.

• Гиперболоидная водонапорная башня 1896 года в Нижнем Новгороде .

• Сетчатая оболочка из Шуховской башни в Москве, чьи участки вдвойне правила.

• Винтовая лестница с линейками внутри Торраццо Кремоны .

• Деревенская церковь в Село, Словения: и крыша (коническая), и стена (цилиндрическая) являются линейчатыми поверхностями.

• Гиперболический параболоид крыша железнодорожной станции Варшава Ochota в Варшаве , Польша.

• Линейчатая коническую шляпу .

• Гофрированная черепица, разделенная параллельными линиями в одном направлении и синусоидальными в перпендикулярном направлении.

• Устройство плоской поверхности путем разметки ( стяжки ) бетона.

Линейчатые поверхности

Первыми известными человечеству поверхностями были плоскость (рис. 3.46 а), цилиндр (рис. 3.46 б), конус (рис. 3.46 в) и сфера (рис. 3.46 г). Архимед присоединил к этому списку «коноиды» (рис. 3.46 д) и «сфероиды» (рис. 3.46 е).

Виды поверхностей

Только П. Ферма у 1643 г. сделал существенный шаг в теорию поверхностей. Он рассматривал любую поверхность как упорядоченную совокупность точек и линий пространства и дал классификацию поверхностей по их характерным признакам.

В 1655 р. Дж. Уоллис определил объёмы и центры тяжести тел, ограниченных кривыми поверхностями.

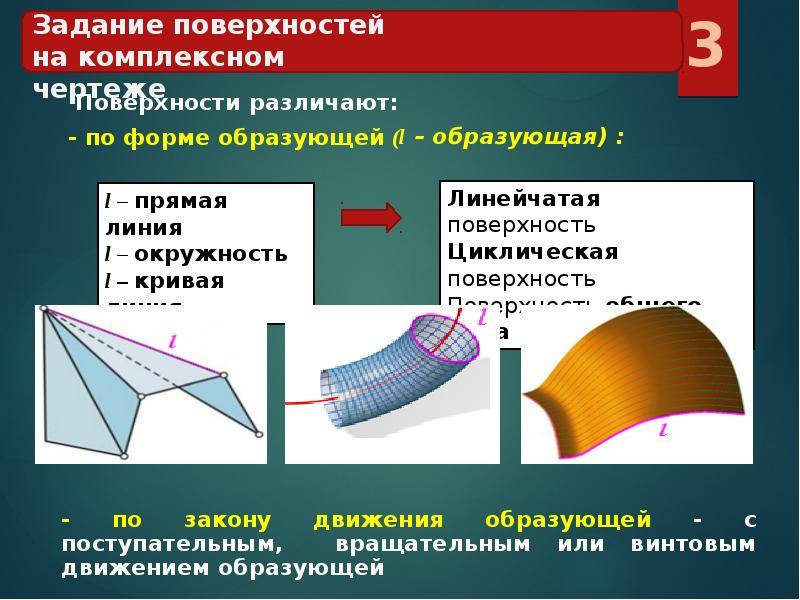
Наиболее применимыми являются такие способы задания поверхностей:

а) аналитический, в котором поверхность задаётся уравнением f(x,y,z) = 0,  связывающим координаты х, у, z каждой точки поверхности;

б) кинематический, согласно которому поверхность создаётся непрерывным движением одной линии l (образующей) вдоль неподвижной линии  (направляющей);

в) каркасный – с помощью множеств характерных точек А (1) , А (2) , … и линий l (1) , l (2) , … поверхности.

Примеры геометрического, кинематического и каркасного способов задания поверхности Ф приведены на рис. 3.47 а – в.

Комплексный чертёж поверхности Ф считается заданным, если одновременно выполняются такие условия:

а) можно построить три проекции l1, l2, l3 образующей линии l;

б) по одной проекции М1 точки М поверхности можно определить другие две её проекции;

в) по двум проекциям А1, А2 точки А на комплексном чертеже можно определить,  принадлежит ли она поверхности Ф, или не принадлежит.

Джон Уоллис (John Wallis) – английский математик, один из предшественников математического анализа, тригонометрии, теории чисел. В 1655 г. издал трактат «Арифметика бесконечного», где ввёл символ бесконечности  и рассчитал интегральные суммы (ещё до существования понятия про интеграл). Ввёл современное понятие математической операции  логарифмирования.

Способы задания поверхностей

Комплексный чертёж поверхности

Например, на рис. 3.48 можно установить проекции образующей l, определить фронтальную проекцию М2 точки М по известной проекции М1. По комплексному чертежу точки А однозначно определяется, что она не принадлежит поверхности. Таким образом, удовлетворив все условия, делается вывод о том, что на рис. 3.48 построен чертёж поверхности Ф.

Разнообразие форм поверхностей создаёт трудности при их изучении. Поэтому целесообразно сделать систематизацию поверхностей. Современное развитие теории поверхностей позволяет классифицировать поверхности по многим критериям. С позиции начертательной геометрии классификация поверхностей такая:

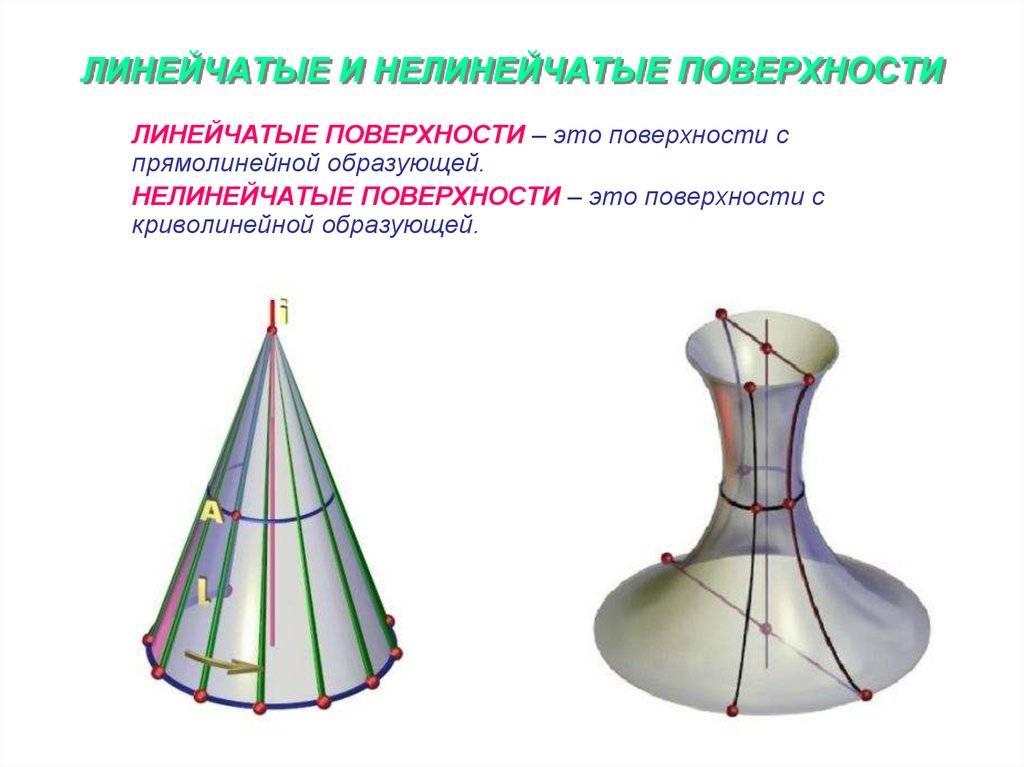
а) линейчатые – поверхности, образованные прямолинейной образующей l:

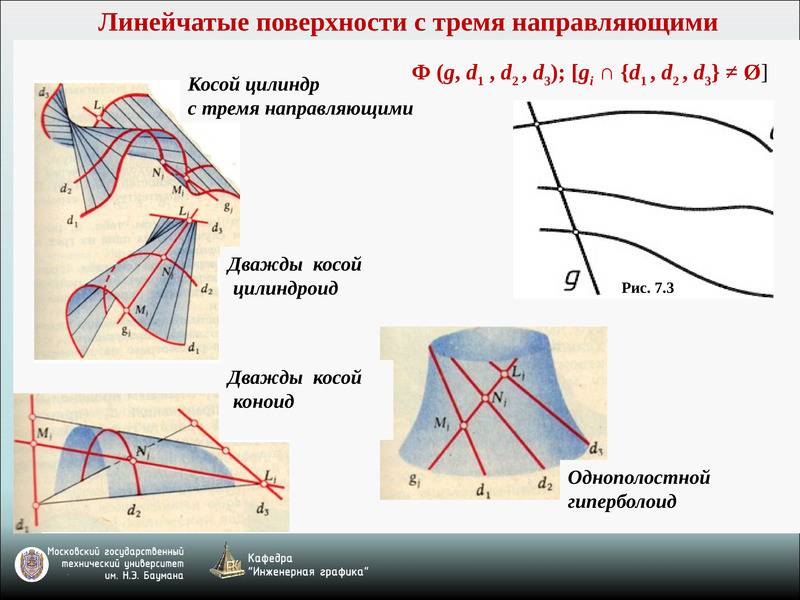
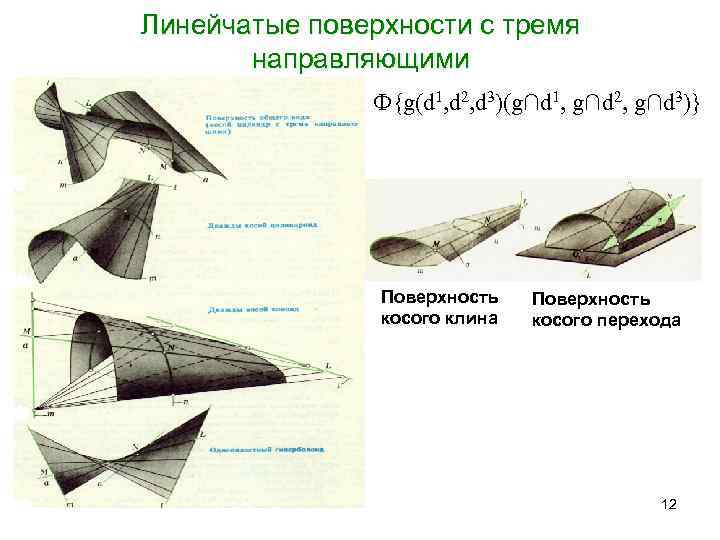
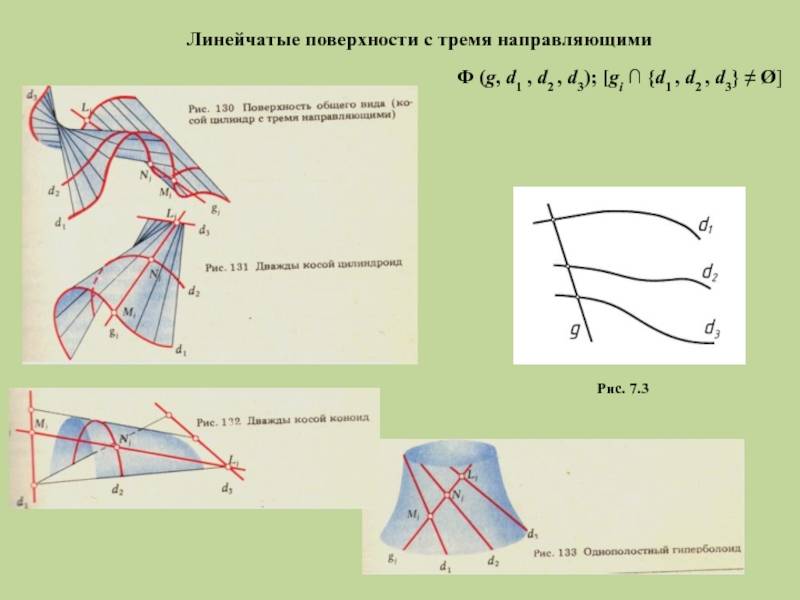
1) с тремя направляющими – образованы движением образующей l, которая одновременно пересекает три направления 

– линейчатая поверхность общего вида;

– конусоид; – косой цилиндр;

– однополостной гиперболоид;

2) с двумя направляющими (див. п. 3.2.1.2):

– цилиндроид;

– коноид;

– гиперболический параболоид;

– геликоид;

3) с одной направляющей (см. п. 3.2.1.3):

– плоскость;

– цилиндр и призма;

– конус и пирамида;

– торс;

б) нелинейчатые:

1) с переменной образующей (см. п. 3.2.2.1);

– поверхность общего вида;

– каналовая поверхность;

2) с постоянной образующей (см. п. 3.2.2.2):

– трубчатая поверхность;

– поверхность перенесения;

– поверхность вращения.

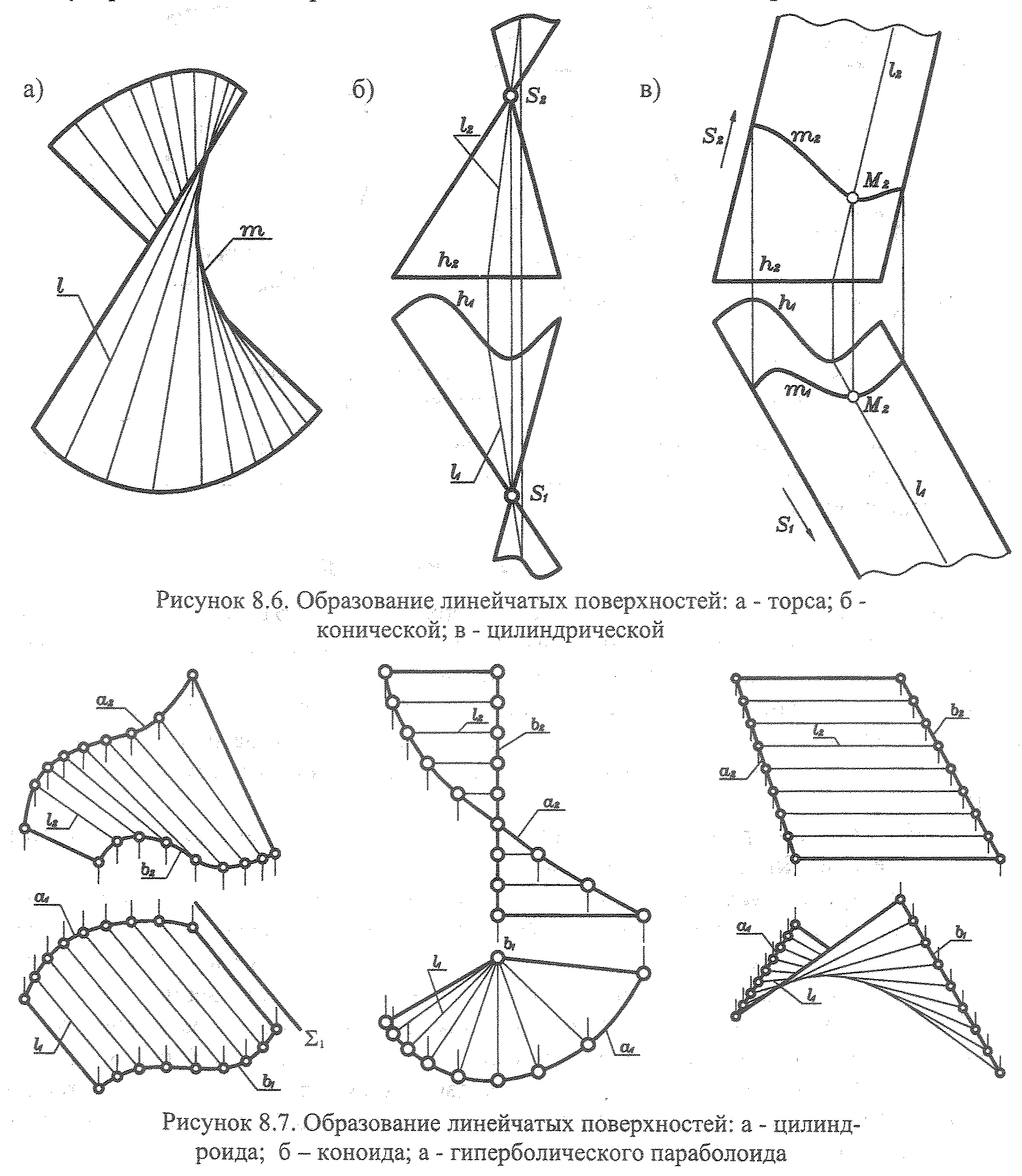
Линейчатая поверхность общего вида – поверхность, образованная движением прямолинейной образующей l, которая в каждом своём положении пересекает три кривые направляющие  (рис. 3.49 а).

Линейчатые поверхности с тремя направляющими

Конусоид – поверхность, образованная движением прямолинейной образующей l,, которая в каждом своём положении пересекает две криволинейные направляющие  и одну прямолинейную направляющую  (рис. 3.49 б).

Косой цилиндр – поверхность, образованная движением прямолинейной образующей l,, которая в каждом своём положении пересекает одну криволинейную направляющую  и две прямолинейные направляющие  (рис. 3.49 в).

Однополостной гиперболоид – поверхность, образованная движением прямолинейной образующей l, которая в каждом своём положении пересекает три прямолинейные направляющие  (рис. 3.49 г).

Линейчатые поверхности широко используются в проектировании архитектурных сооружений башен, павильонов, каркасов крыш зданий и т.д..

На рис. 3.50 приведены примеры сооружений, построенных по методу В. Г. Шухова – ученого, который впервые предложил строить каркасы сооружений в форме однополостного гиперболоида.

Сооружения, построенные по методу В. Г. Шухова

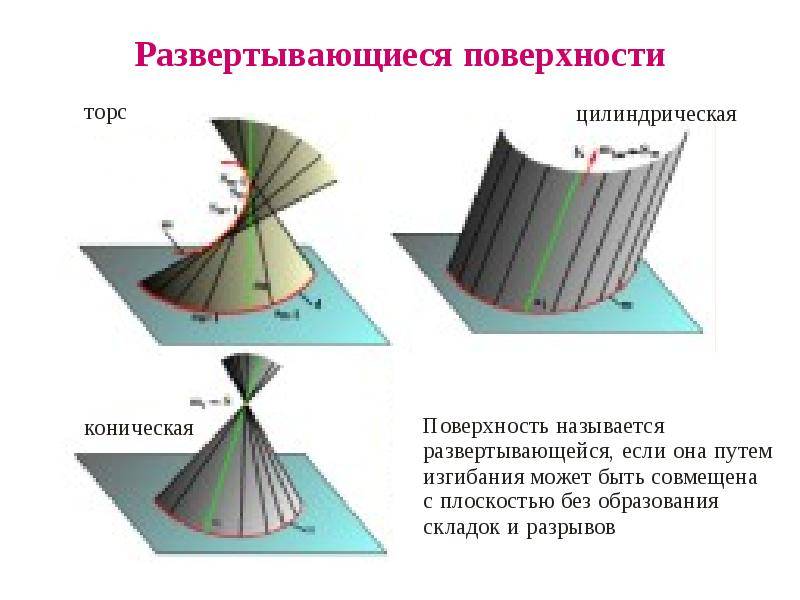
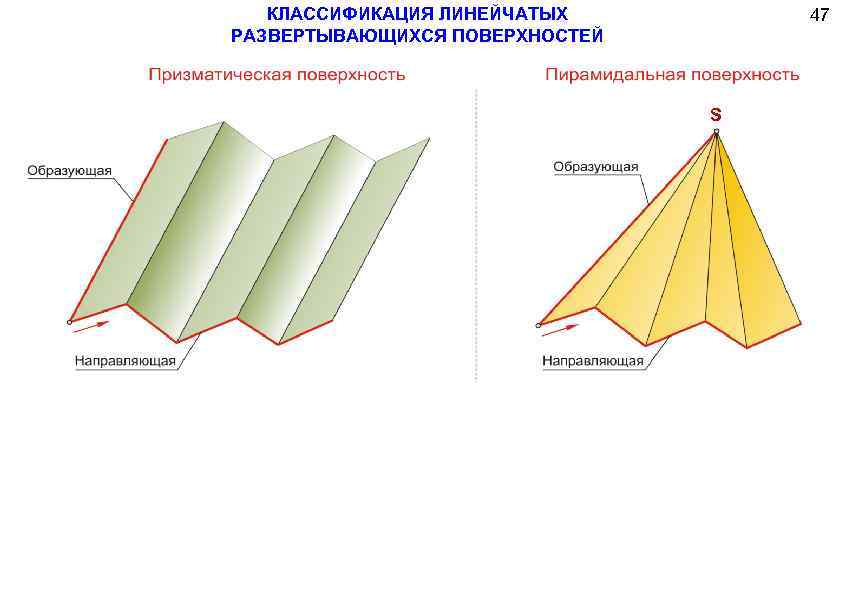
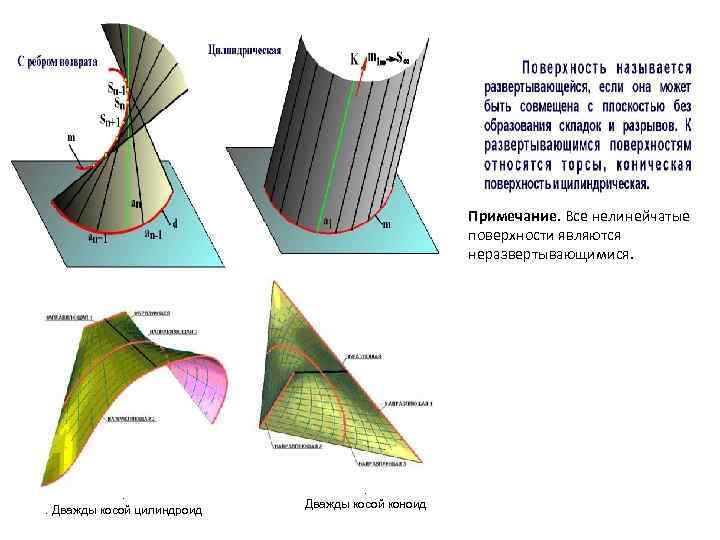
Развертывающиеся поверхности

Эти объекты важны для листопрокатного производства, текстильной промышленности, авиа- и автомобилестроения. Представление о них основывается на допущении, что они обладают гибкостью, но они нерастяжимы и несжимаемы. Под развертывающимися понимают области, которые, изгибая, можно совмещать с плоскостью без порывов, перегибов и складок. Таким образом получается развертка. Это свойство характерно для многогранных объектов и объектов, которые имеют ребра возврата.

Ребро возврата – это направляющая кривая в пространстве, которую касается прямая при передвижении. В системе отсчета развертывающаяся линейчатая поверхность определяется ребром возврата. Указанными характеристиками обладают: торс, а также его частные случаи: объекты, имеющие форму конуса, цилиндра, призмы, пирамиды.

Торс

Торсы используются при проектировании деталей и узлов в машиностроении. Образование линейчатых поверхностей, имеющих вид торса, происходит при передвижении образующей, которая во всех позициях проходит по касательной относительно ребра возврата. Оно, совместно с движущейся прямой, определяет торс в пространстве. Этот геометрический объект составляют две полости, граничащие по ребру возврата.

 

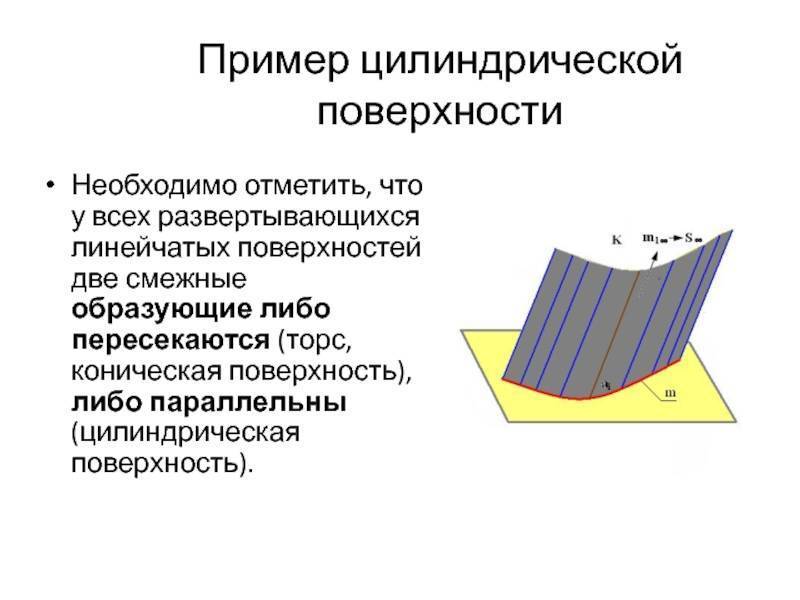
Цилиндрическая

Это особый вид торса. При этом ребро возврата переродилось в несобственную точку, удаленную на бесконечное расстояние. Построенная прямая образующая движется параллельно самой себе по установленной кривой. Чтобы определить цилиндрическую поверхность надо задаться: вектором перемещения и криволинейной траекторией движения.

Коническая

В ней ребро возврата преобразовалось в собственную точку, через которую, по определенной кривой, проходит образующая. Эта точка служит вершиной конуса. Такой объект может складываться из двух полостей. Для его определения задаются указанными точкой и кривой.

Призматическая и пирамидальная

Призматическая отличается от цилиндрической тем, что движение прямой происходит не по кривой траектории, а по ломанной. Ребро возврата преобразовалось в несобственную точку, которая находится на бесконечном расстоянии.

Пирамидальная и конусная различаются формой траектории движения прямой. У конусной – траектория движения криволинейная, у пирамидальной – ломанная.

У перечисленных видов две смежные прямые могут:

• пересекаться (торс, коническая, пирамидальная);
• быть параллельными (цилиндрическая, призматическая).

Чтобы получить уравнение поверхности развертывающейся надо решить систему двух уравнений:

1. уравнения образующей.
2. уравнения направляющей.

Рассмотренные объекты могут быть замкнутыми, если траектория имеет форму окружности или замкнутого многоугольника.

Приложения

Промышленное котельное производство

Изделие котельное (производство: Olivier Roger). Линейчатые поверхности на фото выглядят серыми.

Котел представляет собой листовой металл (листовой металл). При формовании листов используются два основных метода: прокатка (или гибка) и гибка .

Катание дает поверхности вращения, части конусов или цилиндров. Следовательно, они представляют собой линейчатые поверхности.

Складывание позволяет приближаться к поверхностям, ограниченным многогранниками, причем складки / ребра соответствуют образующим поверхности, к которой нужно приблизиться.

Серые части на прилагаемом фото – линейчатые поверхности котельной.

4.1 Классификация поверхностей и их изображение на чертеже

• для построения проекций точек на поверхности цилиндра и конуса используются их образующие и параллели;
• положение точки на поверхности вращения определяется при помощи окружности, проходящей через эту точку на поверхности вращения. Для построения проекций точки поверхности вращения используются параллели;
• для построения проекций точек на поверхности многогранника используются любые вспомогательные прямые линии, принадлежащие граням.

Пример
	Построить линию пересечения поверхности треугольной пирамиды с фронтально проецирующей плоскостью Ф. На рис. 65 представлены две проекции треугольной, пирамиды. Фронтально проецирующая плоскость Ф″ пересекает грани пирамиды по прямым, которые определяются по точкам пересечения ребер пирамиды с секущей плоскостью Ф″. Фронтальные проекции точек пересечения ребер с плоскостью находятся сразу, а горизонтальные проекции точек пересечения определяются в проекционной связи по линиям связи. Линией пересечения является замкнутая ломаная линия, часть которой, принадлежащая грани SAC, является невидимой.
Рис.65. Построение линии пересечения пирамиды

• для нахождения линии пересечения любой другой поверхности плоскостью надо использовать вспомогательные секущие плоскости. Точки искомой линии определяются в пересечении линий, по которым вспомогательные секущие плоскости пересекают поверхность и плоскость;

  вспомогательную секущую плоскость следует выбирать так, чтобы её линия пересечения с поверхностью проецировалась на плоскости проекций в виде прямой или окружности;

• для построения точек пересечения прямой с поверхностью необходимо через прямую провести вспомогательную секущую плоскость и найти линию пересечения этой плоскости с поверхностью; точки пересечения заданной прямой и построенной линией на поверхности и будут искомые точки пересечения прямой с поверхностью.
  

  Пример
  	Определить точки пересечения прямой АВ с поверхностью вращения. На рис. 66 представлены горизонтальная и фронтальная проекции поверхности вращения и прямой АВ. Проведем через прямую АВ фронтально проецирующую плоскость Ф и построим линию пересечения этой плоскости с поверхностью вращения. След плоскости Ф″ пройдет через фронтальную проекцию прямой A″ B″. Для построения линии пересечения плоскостиФ″ и поверхности вращения проведем параллели поверхности вращения и построим горизонтальные проекции точек пересечения параллелей с плоскостью Ф″. Полученные точки соединим кривой линией и на пересечении горизонтальных проекций построенной линии и прямой найдем точки Mи Nпересечения прямой АВ с поверхностью вращения.
  Рис.66. Пересечение прямой с поверхностью

  ЗАДАЧИ
  Задача 50	Лежит ли точка А на поверхности усеченного конуса?
  Задача 51	Построить проекции линии пересечения плоскостей Ф1,Ф2,Ф3 с поверхностью цилиндра, конуса, сферы.
  Задача 52	Найти точки пересечения прямойАВ с поверхностью вращения.
  Задача 53	Найти точки пересечения прямой АВ и прямой CD с поверхностью прямого кругового цилиндра. Построить три проекции линии, лежащей на поверхности цилиндра. Определить видимость проекций линии.
  Задача 54	Найти точки пересечения прямой АВ и прямой CD с поверхностью прямого кругового конуса и построить три проекции линии, лежащей на поверхности конуса. Определить видимость проекций линии.
  Задача 55	Найти точки пересечения прямой АВ и прямой CD с поверхностью сферы и построить три проекции линии, лежащей на поверхности сферы. Определить видимость проекций линии.

Параметрическое представление

Пример линейчатой ​​поверхности.

Мы можем описать линейчатую поверхность S , рассматривая его как в виде семейства линий D ( U ) в зависимости от параметра у обхода части I множества действительных чисел . Для этого достаточно , чтобы дать для каждого U в I точку P ( U ) и направляющий вектор из D ( ¯u ). Тогда мы получим параметрическое представление поверхности S  : V(ты)→{\ displaystyle {\ overrightarrow {V (u)}}}м∈S⟺∃ты∈я∃v∈рM(ты,v)знак равноп(ты)+vV(ты)→.{\ Displaystyle м \ в S \ iff \ существует и \ в я \ четырехъядерный \ существует v \ в \ mathbb {R} \ четырехъядерный M (u, v) = P (u) + v \, {\ overrightarrow {V ( u)}}.}

Дуга установлено с помощью называется директрисой кривой из S . ты∈я↦п(ты)∈р3{\ Displaystyle и \ ин I \ mapsto P (u) \ in \ mathbb {R} ^ {3}}

В примере напротив мы взяли п(ты)знак равно(ты,-ты2,ты3)етV(ты)→знак равно(-ты2,1,ты).{\ Displaystyle P (u) = (u, -u ^ {2}, u ^ {3}) \ quad {\ rm {et}} \ quad {\ overrightarrow {V (u)}} = (- u ^ {2}, 1, u).}

Применение и история разворачивающихся поверхностей [ править ]

Развивающееся соединение двух эллипсов и его развитие

Детерминантное условие для развертывающихся поверхностей используется для определения численно складываемых связей между пространственными кривыми (директрисами). На схеме показана развивающаяся связь между двумя эллипсами, находящимися в разных плоскостях (одна горизонтальная, другая вертикальная), и ее развитие.

Впечатление об использовании развертываемых поверхностей в автоматизированном проектировании ( САПР ) дается в документе « Интерактивное проектирование развертываемых поверхностей»

Историческое исследование по развёртывающимся можно найти в развертывающейся поверхности: их история и применение

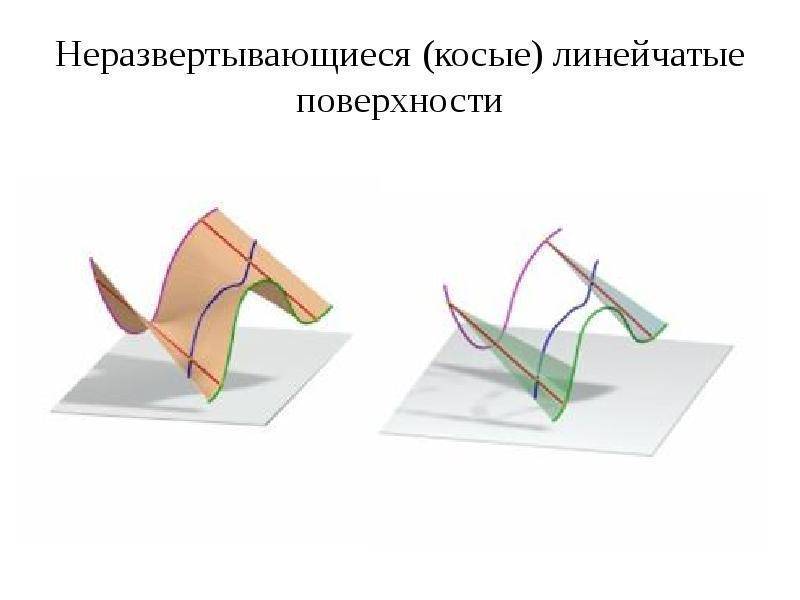
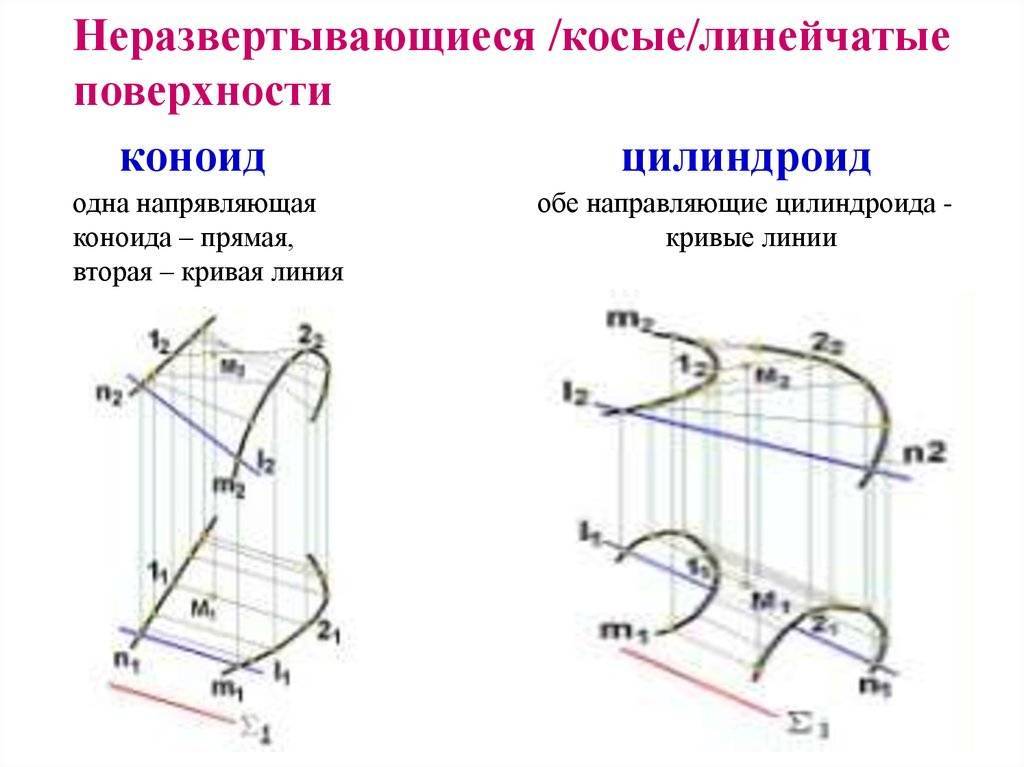
Неразвертывающиеся или косые поверхности

Их появление часто вызвано передвижением прямолинейной создающей вдоль пути, развитой тремя направляющими. Они непосредственно формируют закон перемещения и бывают прямыми или кривыми. Есть индивидуальные ситуации, когда траектория движения устанавливается:

• 2-мя направляющими и произвольной плоскостью;
• направляющими свободной формы и плоскостью параллелизма (к примеру, область проекции).

Направляющая поверхность замещает одну из линий пути. С ней двигающаяся прямая составляет постоянный угол.

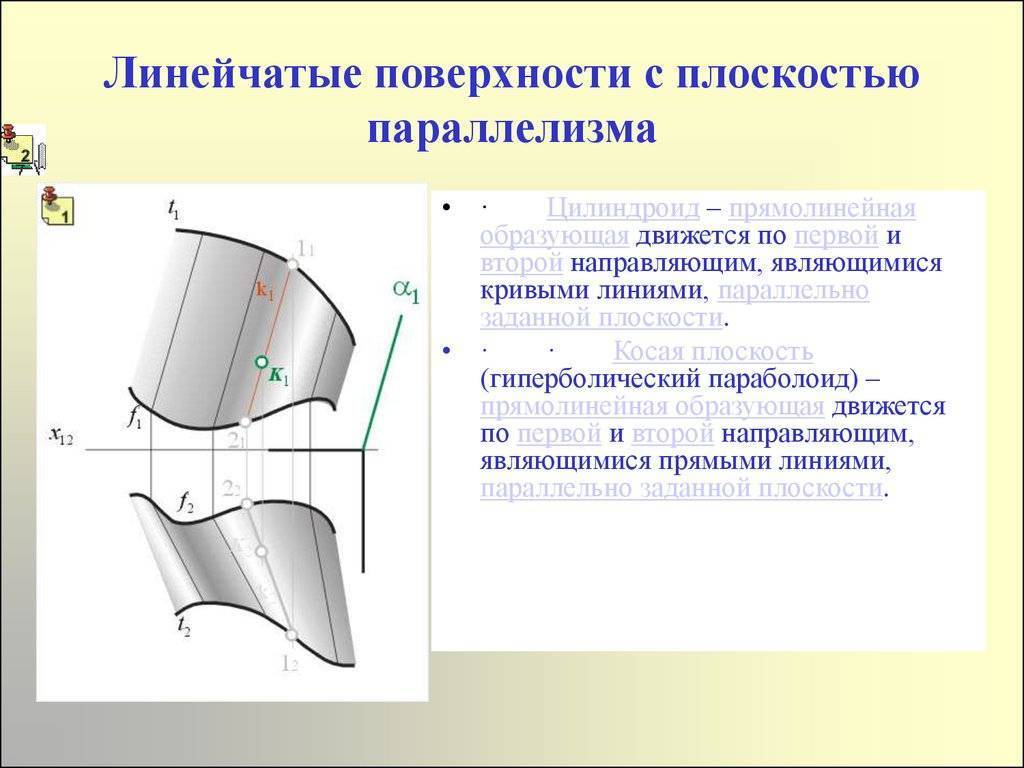
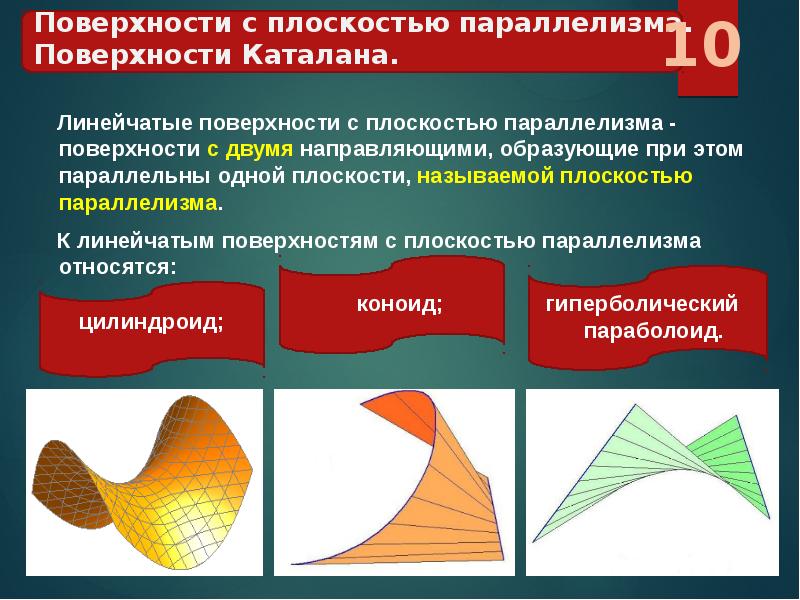
Варианты подобных объектов: цилиндроид, коноид, гиперболический параболоид. Их главные характеристики приведены в таблице.

Вид	Определители (вместе с плоскостью параллелизма)	Характеристика	Некоторые сфере использования
Цилиндроид	2 кривые направляющие	Изобразить образующие на комплексных чертежах можно так: 1.Параллельно параллелизму провести серию плоскостей. 2.Определить точки, в которых кривые направляющие цилиндроида пересечены с плоскостями. Если за параллелизм принять одну из плоскостей уровня, что делает легче построение, то линии будут подходить линиям уровня.	Проектирование больших, крупного диаметра, воздушных каналов
Коноид	2 направляющие: · откровенная	1. Особенный случай цилиндроида. 2. Прямой коноид имеет направляющую прямолинейную, расположеную под прямым углом к области параллелизма.	Гидротехническое строительство, на конструкторском уровне опор мостов
Параболоид гиперболический (синонимично понятию косой плоскости)	2 пересекающиеся прямые направляющие	1. Изображается как несколько прямых по закону: создающая должна пересекать направляющие и проходить параллельно установленной области параллелизма. 2. При пересечении некоторыми плоскостями в сечениях получаются гиперболы и параболы.	При разрабатывании конструкций гидротехнических строений, дорог, откосов, шлюзов, каналов, крыльев ветряков

Линейчатые поверхности собой представляют математические абстракции, посредством которых можно получить представление о характеристиках предметов.

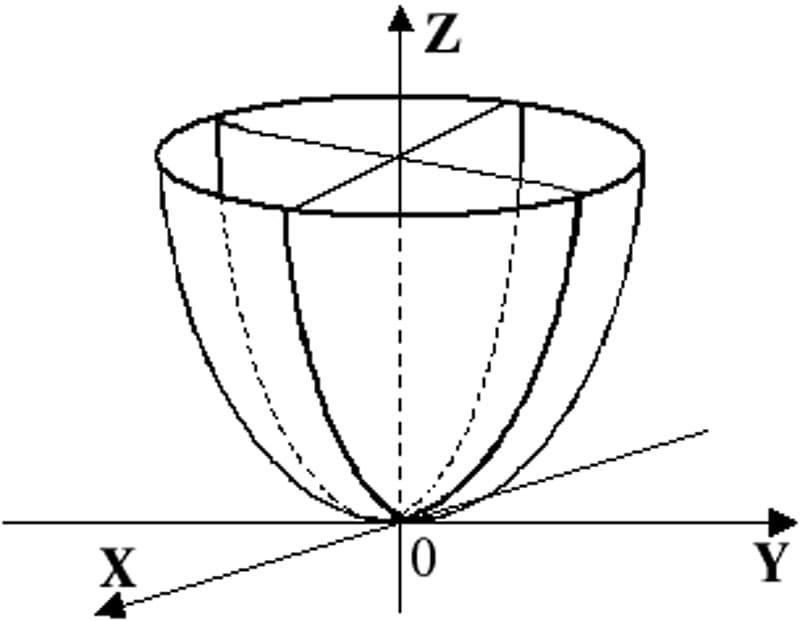
Их моделирование, математическое, геометрическое описание дают возможность проектировать разные тела и конструкции в автомобилестроении, архитектуре. Современные программы компьютерного проектирования, к примеру КОМПАС 3D, упрощают и автоматизируют процесс моделирования подобных объектов.

Если вы нашли погрешность, пожалуйста, выдилите фрагмент текста и нажмите Ctrl+Enter.

7.3. Цилиндрическая поверхность

Цилиндрическая поверхность образуется движением прямой линии, которая в любом своём положении параллельна данному направлению и пересекает криволинейную направляющую (Рисунок 7.6).

Цилиндр – геометрическое тело, ограниченное замкнутой цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими все образующие данной поверхности.

Взаимно параллельные плоские фигуры, ограниченные цилиндрической поверхностью, называются основаниями цилиндра.

Если нормальное сечение (плоскость сечения перпендикулярна образующим) имеет форму окружности, то цилиндрическая поверхность называется круговой.

Если образующие цилиндрической поверхности перпендикулярны к основаниям, то цилиндр называется прямым, в противном случае – наклонным.

Рассмотрим проецирование прямого кругового цилиндра  и принадлежащей ему точки F.

Условимся, что фронтальная проекция точки F – невидима (Рисунок 7.6).

Рисунок 7.6 – Проецирование цилиндра на плоскости проекций

Горизонтальная и профильная проекции точки F будут видимы.

При определении видимости, образующие, которые находятся на части, обращённой к наблюдателю и обозначенной на π1 сплошной зелёной  линией – на плоскости проекции π2 видны, а которые находятся на части, обозначенной толстой штриховой линией – видны на π3.

Пусть точка А на π2 видима (Рисунок 7.7). Тогда на π1 она будет видима, а на π3 невидима.

Рисунок 7.7 – Эпюр прямого кругового цилиндра и принадлежащих ему точек

Что собой представляет эта технология?

Специфика метода заключается в построении 3D объектов, с помощью специальных плоскостей (полигонов). С его помощью в 3D Max, можно создавать ряд объектов, без которых любой интерьер был бы пустым. В 3D Max полигональное моделирование, выполняет основную функцию, без этого способа построение объектов становится не возможным. Любые полигональные фигуры, состоят из граней плоскостей (полигонов), объединённых в один элемент с помощью вершин:

• Ребро – представляет собой линию, выступающую за границу грани;
• Грань (полигон) – плоскость, состоящая из треугольных или четырёхугольных ячеек, образующих сетку. Количество ячеек неограниченное;
• Вершина – точка, соединяющая рёбра.

Все объёмные тела имеют свой каркас, который составляет основу модели: с его помощью можно редактировать изделие, менять форму, вытягивать, передвигать и т. п. В проектировании архитектурных сооружений, дизайне малых форм и т. п, там, где требуется передать точное сходство с прототипом, часто применяется метод полигонального моделирования.

На начальном этапе конструирования, создаются низкополигональные модели, что даёт возможность сократить время на обработку данных. При этом уровень детализации будет невысоким. Что бы создать модель с более проработанной детализацией, необходимо увеличить число полигонов, такое изделие будет называться высокополигональным. Метод применяется, когда необходимо создать точную копию объекта.

Конструирование происходит в несколько уровней, по стандартной схеме, путём постепенного увеличения полигонов.

• Сначала, создаётся базовая форма изделия.
• После этого, добавляются фаски для уточнения формы.
• И в завершении, прорабатываются все детали, поверхность сглаживают.

Несмотря на то, что полигональное моделирование считается самым распространённым способом построения 3D объектов, но это не единственный метод, используемый в создании трёхмерных изображений. Так, например: при проектировании объектов животного мира или растений, лучше всего использовать сплайновое моделирование.

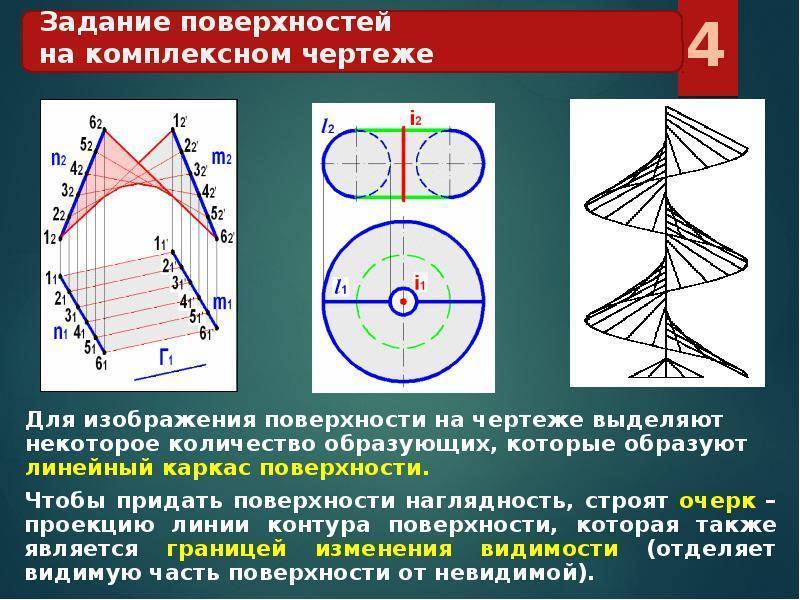
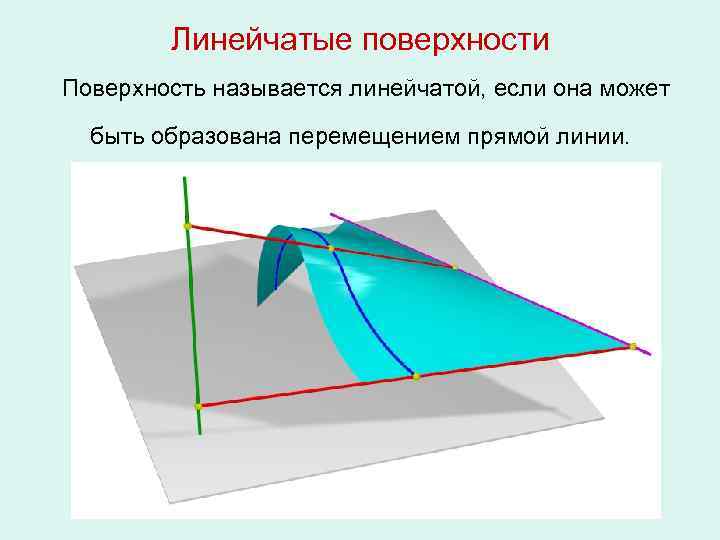
Линейчатые поверхности. Принадлежность линии и точки к поверхности

Линейчатой называется поверхность, образующей которой является прямая линия.

В общем случае линейчатая поверхность однозначно определяется тремя направляющими линиями .

Задать поверхность на чертеже – значит указать условия, позволяющие построить каждую точку этойповерхности. Для задания поверхности достаточно иметь проекции направляющей линии и указать, как строится образующая прямая, проходящая через любую точку направляющей. Однако, для придания наглядности изображения, вычерчивают очерк, линии видимости и строят точки на поверхности.

Коническая поверхность образуется прямой линией, проходящей через некоторую неподвижную точку и последовательно через все точки некоторой кривой направляющей линии. Если направляющей линией является окружность, то поверхность называется наклонным или эллиптическим конусом.

На рис. 3.10 представлены: направляющая окружность – m; неподвижная точка – S; прямолинейная образующая — l . Это первая часть определителя – геометрическая. Образующая движется по направляющей, оставаясь неподвижной в точке S. Описание закона движения является алгоритмической частью определителя. При этих условиях поверхность на чертеже считается заданной. Для придания наглядности, на рис. 3.11 построены очертания поверхности, линии видимости и промежуточная точка, принадлежащая поверхности.

Построение точек, принадлежащих поверхности, осуществляется следующим образом. Пусть задана фронтальная проекция точки А (А»). На фронтальной плоскости она изображена как невидимая. Для построения ее горизонтальной проекции через точку задаем линию, принадлежащую поверхности. Этой линией будет окружность, так как линия задана параллельно основанию, а основанием является окружность. Центр окружности лежит на осевой линии поверхности. Проводим линию связи из центра окружности на горизонтальную плоскость до пересечения с горизонтальной осевой поверхности. Строим окружность, которой принадлежит точка А.. По линии связи отмечаем ее местоположение с учетом видимости для горизонтальной плоскости, где точка является видимой. Аналогичные построения выполняются для наклонного (эллиптического) цилиндра.

Тема 4

Позиционные задачи

Все задачи начертательной геометрии условно могут быть разделены на метрические и позиционные. К метрическим задачам относятся задачи на измерение линейных и угловых величин. Решение этих задач будет рассмотрено ниже.

К позиционным задачам относятся задачи на принадлежность и взаимное пересечение геометрических фигур. По существу решение позиционных задач сводится к нахождению точек одновременно принадлежащих двум или более фигурам. Задачи на определение принадлежности одной геометрической фигуры к другой частично уже рассмотрены:

o принадлежность точки к прямой (рис. 1.23) .

o принадлежность линии к поверхности. Рис. 3.9 ;

o принадлежность точки к поверхности. Рис. 3.11

Задачи на построение линий пересечения геометрических фигур условно можно разделить на три группы:

o пересечение плоскости с поверхностью;

o пересечение прямой линии с плоскостью и с поверхностью.

o взаимное пересечение поверхностей.

Решение всех типов позиционных задач на пересечение подчиняются общему алгоритму. На рис. 4.1 представлена поверхность полусферы и усеченного конуса. Для построения точек, одновременно принадлежащих этим поверхностям, воспользуемся общим алгоритмом.

1. Вводится вспомогательная поверхность, в частном случае — плоскость. Эта вспомогательная поверхность назначается таким образом, чтобы она пересекла обе фигуры по простым для построения линиям — по прямым или по окружностям.

2. Строятся линии пересечения вспомогательной поверхности с каждой из заданных фигур.

3. Отмечаются точки взаимного пересечения построенных линий. Эти точки принадлежат обеим фигурам, следовательно, являются элементом пересечения фигур.

4. Соединяют точки в определенной последовательности и определяют видимость линии пересечения и фигур друг относительно друга.

Находить точки для построения линии взаимного пересечения фигур надо в определенной последовательности.

1. В первую очередь отмечают точки на контурных образующих или на ребрах, если поверхностигранные.

2. Находят экстремальные точки: наивысшую; наинизшую; самую левую; самую правую; самую ближнюю и самую дальнюю.

3. Отмечают точки на линиях среза (принадлежащие основаниям).

4. Если построенных точек недостаточно для выявления формы линии взаимного пересечения, строят ряд промежуточных (случайных) точек.

голоса

Рейтинг статьи