Эвольвентное зубчатое зацепление

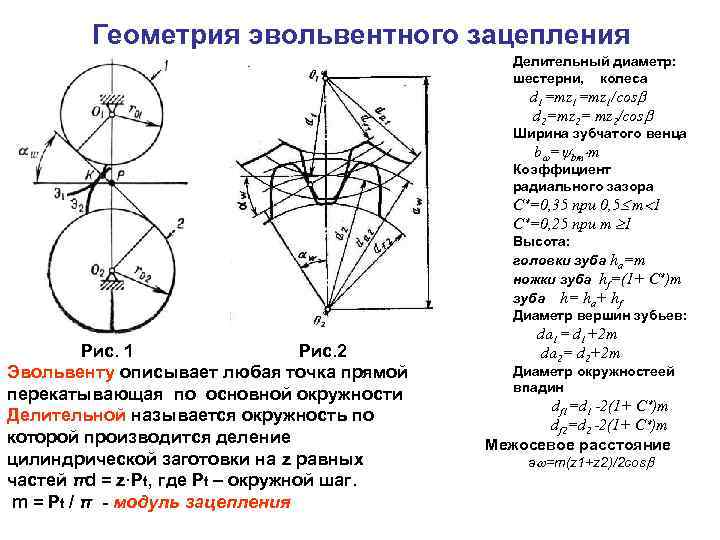
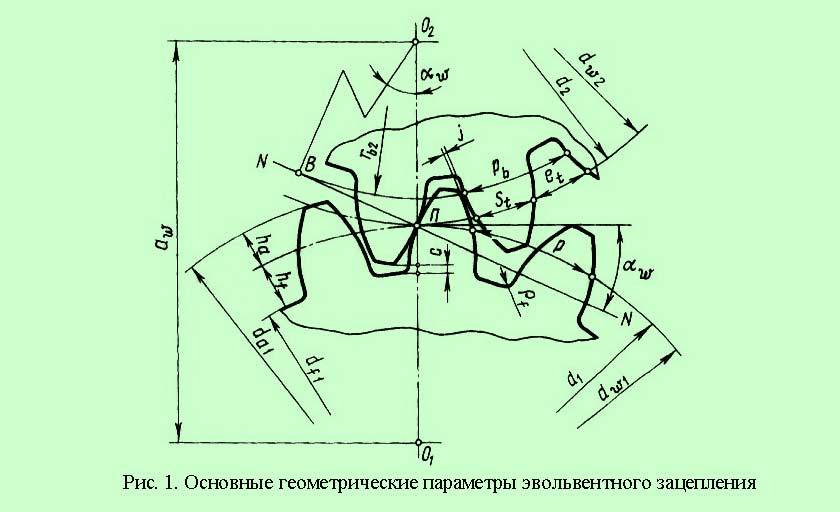
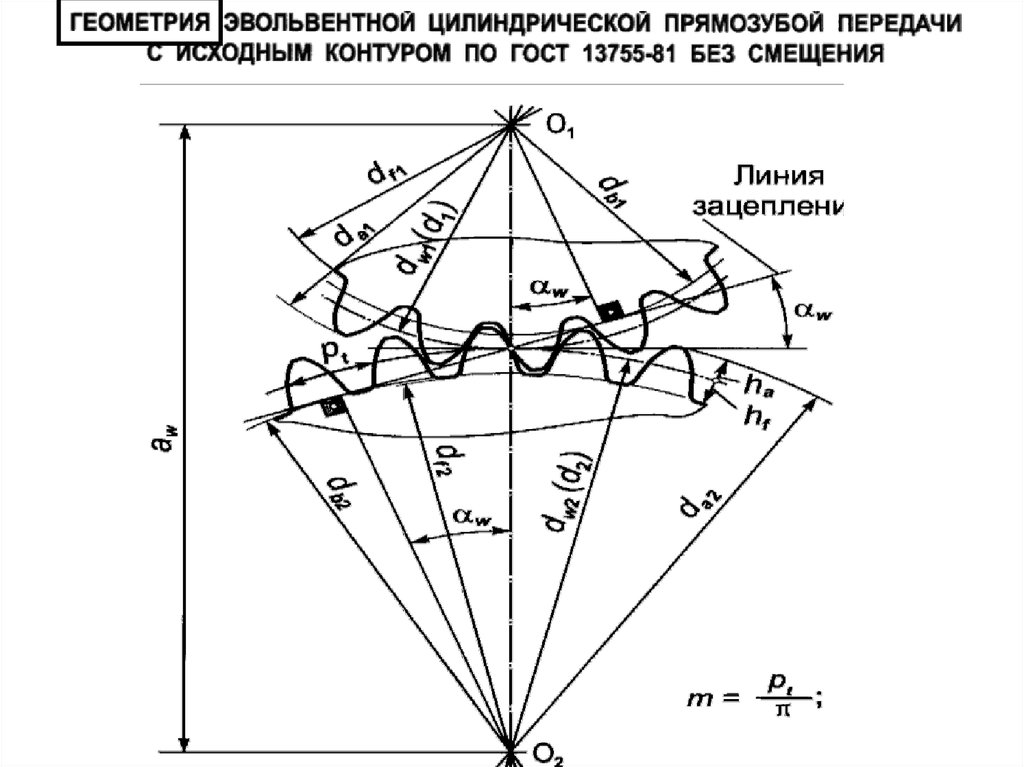
Обозначение шлицевых эвольвентных соединений

Варианты условных обозначений эвольвентных шли­цевых соединений на чертежах показаны на рис 17.

Центрирование по боковым сторонам

Рисунок 17. Шлицевое эвольвентное соединение при центрировании по боковым сторонам зубьев.

Шлицевое эвольвентное соединение с D = 65мм; т = 3 мм, при центрировании по боковым сторонам зубьев с посадкой 9H/9g.

Центрирование по наружному диаметру:

Центрирование по внутреннему диаметру:

здесь: D=65, m=3, центрирование по внутреннему диаметру с посадкой H7/g6, посадки остальных поверхностей предусмотрены в табл.5.

Предельные значения радиального биения должны соответствовать значениям табл…., а ориентировочно это половина суммарного допуска

T ( т.е. Fr = 0,5 T ).

Пример выбора параметров эвольвентного шлицевого соединения.

Для подвижного шлицевого соединения D = 50 мм, с модулем т = 2 мм, без повышенных требований к соосности, выбрать геометрические параметры, определить предельные размеры вала и втулки, представить схему расположения полей допусков с оценкой предельных зазоров.

Принимаем центрирование шлицевого соединения по боковым поверхностям зубьев. По номинальному (исходному) диаметру соединения D = 50 мм и модулю т = 2 мм, по табл. 2 определяем число зубьев z = 24.

• Геометрические параметры получаем в соответствии с табл. 1,
• где:
• для вала толщина зуба по делительной окружности
• s =(π/2) m+2 Xm tgα,
• здесь смещение исходного контура будет:

Xm=0.5(D — m z -1.1 m)

Xm=0.5 · (50 — 2·24 -1.1·2) = -0,1мм

1. Теперь:
2. s =(3,1415/2) · 2+2· (-0,1) · 0,5773
3. s =3,1415+(-0,11547)=3,026мм
4. для шлицевой втулки ширина впадины по делительной окружно­сти
5. s=e=3,026мм
6. диаметр окружности вершин зубьев:
7. da =d-0,2m
8. da =50-0,2·2=49,6 мм.
9. диаметр окружности вершин зубьев втулки
10. Da = D – 2m
11. Da = 50 – 2·2 = 46мм.
12. Диаметр делительной окружности вычисляем
13. d = mz = 2·24 =48мм.

Принимаем плоскую форму дна впадины и согласно примечанию к табл. 4. определяем, диаметр окружности впадин вала

• df тах = D­- 2,2т = 50 — 2,2·2 = 45,6 мм
• Диаметр окружности впадины втулки будет
• Df = D = 50 мм.

Учитывая заказанную подвижность соединения выбираем посадки с зазорами. на каждый размер шлицевых деталей по табл.4.

Для центрирования по боковым сторонам предусмотрены предпочтительные посадки 9H/9h и 9H/9g,больший зазор у 9H/9g, её принимаем и получаем формулу соединения.

По таблице приложения 22 выписываем параметры, для шлицевой втулки c полем 9H при D = 50 мм, и модуля т = 2 мм, ES=+71, ESe=+26, EI=0, для шлицевого вала c с полем 9g: es=-11, ese=-37, ei=-82.

Для большего диаметра примем посадку H16/d9 по таблице 4. Параметры шлицевой втулки по Df=50 ,будут определены по таблицам приложения: EI=0, ES=+1600, шлицевого вала по da= 49,6,es=-80,ei=-142.

Для меньшего диаметра по табл. 4 принимаем посадку H11/h16 определяя характеристики по таблицам допусков и посадок, приложения. Параметры шлицевой втулки при Da=46, будут EI=0, ES=+160, шлицевого вала при df= 45,6, es=0, ei=-1600мкм,

По полученным значениям отклонений не трудно получить предельные размеры поверхностей соединения. Результаты удобно представить в виде таблицы табл.6. Подсчитываем предельные размеры и допуски, занося в таблицу.

Таблица 6. Результаты.

Параметр мм	Поле допуска	Предельные отклонения мкм	Предельные размеры мм	Допуск мм
ES (es)	ESe (ese)	EI (ei)	max	min
Шлицевый вал
s=3,026	9g	-11	-37	-82	2,989	2,944	0.045
da=49,6	d9	-80	—	-142	49,520	49,458	0,062
df=45,6	h16	—	-1600	45,6	44,0	1,6
Шлицевая втулка
e=3,026	9H	+71	+26	3,097	3,052	0,045
Df=50	H16	+1600	—	51,6	50,0	1,6
Da=46	H11	+160	—	46,16	46,0	0,16

Схемы расположения полей допусков изображены на рис.9.

1. Рисунок 18. Графическое представление посадок шлицевого соединения 65x3x 9H/9g Гост 6033-60
2. Определяем наибольший Smax и наименьший Smin зазоры для посадки 9H/9g по боковым поверхностям зубьев:
3. Smax =eimax — Smin = 3,097 — 2,944 = 0,153мм;
4. Smin =eimin — Smax = 3,052 — 2,989 =0,063 мм.



Построение эвольвентного зацепления

Существует несколько способов построения эвольвентного зацепления, используемого для изготовления зубчатых колес, которые можно выполнять вручную или с помощью систем автоматического построения.

При проектировании зацепления зубчатых колес учитывают не только геометрические параметры, но и технологические процесс изготовления, а также желаемые динамические и прочностные показатели готового механизма.

Построение эвольвенты зубчатого колеса состоит из нескольких этапов:

1. Графическое построение окружности радиусов (определяется исходя из необходимого количества зубьев и прочностных характеристик готового механизма).
2. Через полюс зацепления проводится прямая в токе касания изначальных окружностей (строится под необходимым углом зацепления).
3. Окружности колес должны соприкасается по полученной прямой. Обкатывание ее по окружности первого колеса, точка, совпадающая с полюсом, образует первую эвольвенту. Такая же манипуляция с колесом 2, позволяет получить вторую эвольвенту.

При производстве шестерен зубья несколькими методами: копирования и обкатки. Если необходимо изготовить мелкую деталь, прибегают к методу формообразования, другими словами – горячей накатки. Такой способ менее точен, но форма фрезы при копировании не позволяет выполнить миниатюрные вырезы.

Метод копирования предусматривает вращение фрезы вдоль поверхности, образующее зубья. Она прорезает одну впадину за один проход между соседними зубьями. Затем фреза возвращается в базовое положение с одновременным поворотом заготовки на необходимый угол шага. Такой способ изготовления довольно точный, но производительность его низкая.

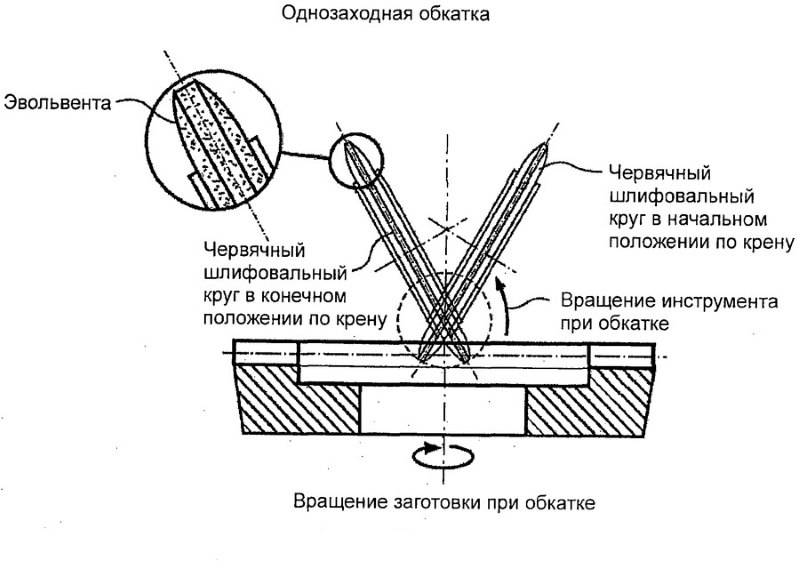
Более совершенным способом является метод обкатки. В его основе лежит огибающее движение, соответствующее желаемому движению зубчатого колеса при зацеплении. Процесс производства похож на движение шестерен в работе. Такое зацепление называется станочным. Рабочий инструмент в таком случае изготавливается в виде круглой, зубчатой фрезы или инструментной рейки.

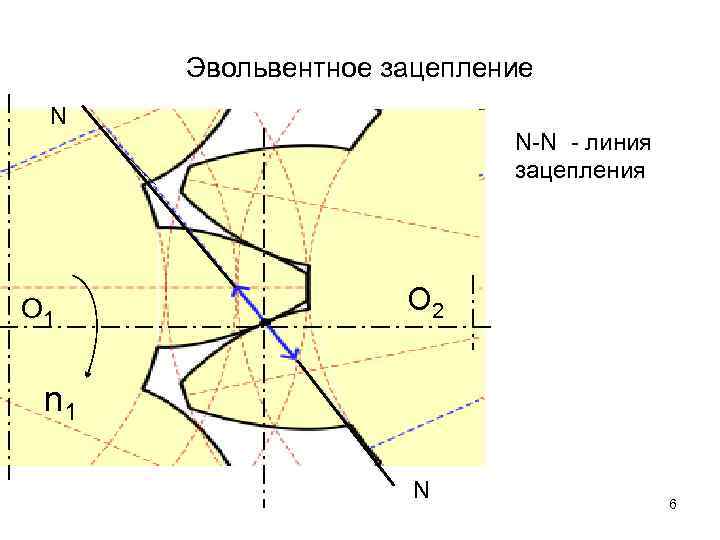
Построение эвольвентного зацепления

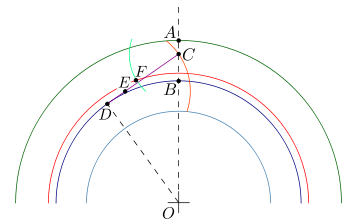
Способ приближённого построения эвольвентного зубчатого зацепления. Подходит для технических рисунков, построенных от руки или с помощью САПР.

Перед построением необходимо задать следующие размеры:

• высота ножки зуба hf{\displaystyle h_{f}} (на рис. обозначена a);
• высота головки зуба ha{\displaystyle h_{a}} (на рис. обозначена b);
• диаметр начальной окружности dw{\displaystyle d_{w}} (на рис. обозначен D);
• угол зацепления α{\displaystyle \alpha } (на рис. обозначен φ);
• окружная толщина зуба s_t;
• радиус кривизны переходной кривой в граничной точке профиля ρ_f.

	Изобразите начальную окружность (pitch circle) с диаметром D, и центром шестерни O. Окружность показана красным цветом. Изобразите окружность вершин зубьев (outside diameter) с центром в точке O с радиусом большим на высоту головки зуба(зелёного цвета). Изобразите окружность впадин зубьев (root diameter) с центром в точке O с радиусом меньшим на высоту ножки зуба (голубого цвета).
	Проведите касательную к начальной окружности (розовая). В точке касания под углом φ проведите линию зацепления (line of action), оранжевого цвета. Изобразите окружность, касательную к линии зацепления, с центром в точке O. Эта окружность является основной (base circle) и показана синим цветом.
	Отметьте точку A на окружности вершин зубьев. На прямой соединяющие точки A и O отметьте точку B находящуюся на основной окружности. Разделите расстояние AB на 3 части и отметьте точкой C полученное значение от точки A в сторону точки B на отрезке AB.
	От точки C проведите касательную к основной окружности. В точке касания отметьте точку D. Разделите расстояние DC на четыре части и отметьте точкой E полученное значение от точки D в сторону точки C на отрезке DC.
	Изобразите дугу окружности с центром в точке E, что проходит через точку C. Это будет часть одной стороны зуба (показана оранжевым цветом). Изобразите дугу окружности с центром в точке C и радиусом, равным толщине зуба. Место пересечения с начальной окружностью (pitch circle) отметьте точкой F. Эта точка находится на другой стороне зуба.
	Изобразите скругление (fillet) между стороною зуба и окружностью впадин зубьев (root diameter). Изобразите радиус профиля зуба — дугу окружности радиусом EC из точки F (отмечено темно зеленым). Отметьте место пересечения радиуса профиля зуба с основной окружностью точкой G (точка G на изображении показана не верно)
	Изобразите радиус профиля зуба — дугу окружности радиусом EC из точки G — это другая сторона зуба. Добавьте скругление у основания зуба к окружности впадин зубьев (как в предыдущем шаге)
	Зуб готов. Наружная окружность между двумя боковыми поверхностями – это вершина зуба. Повторите операцию для каждого зуба.

Перед построением эвольвентного зацепления необходимо рассчитать его геометрические параметры. Предположим, что даны числа зубьев колеса z1{\displaystyle z_{1}} и шестерни z2{\displaystyle z_{2}}, указан тип зацепления: нулевое, равносмещенное или неравносмещенное.
Сначала исходя из типа по таблицам или блокирующему контуру нужно выбрать коэффициенты смещения x1{\displaystyle x_{1}} и x2{\displaystyle x_{2}}.

Исходные данные и замеры

На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.

Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.

Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.

Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.

Результаты расчетов

Для более крупных потребуются измерения и вычисления.

Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:

m=De/(z+2)

Последовательность действий следующая:

• измерить диаметр штангенциркулем;
• сосчитать зубцы;
• разделить диаметр на z+2;
• округлить результат до ближайшего целого числа.

Зубец колеса и его параметры

Данный метод подходит как для прямозубых колес, так и для косозубых.

Построение эвольвенты окружности по заданному диаметру

Построение эвольвенты окружности.

1. Делим окружность на произвольное число равных частей.

2. Проводим касательные к окружности в точках деления. Направляем их в одну сторону.

3. На касательной, проведенной через последнюю точку деления, откладываем отрезок, равный длине окружности

4. Делим отрезок на то же число равных частей, что и окружность.

5. На первой касательной откладываем одно деление отрезка.

6. На второй касательной откладываем два деления отрезка.

7. На третьей касательной откладываем три деления отрезка и т. д.

Получаем точки I, II, III и т.д. Соединяем эти точки по лекалу.

Касательная к эвольвенте ( в примере в точке Х) перпендикулярна к касательной 10-Х окружности.

Эвольвента. Построение эвольвенты окружности.

Другие геометрические построения и формулы здесь.

Определение скоростей и угловых скоростей звеньев механизма.

1. Известны длины звеньев механизма, величина и направление угловой скорости ведущего звена, Расчет начинаем вести с ведущего звена механизма. Установив вид движения звена, записываем соответствующую зависимость. В нашем случае кривошип совершает вращательное движение.

Угловая скорость постоянна, поэтому скорость точки А определяется по формуле:

где . Из точки О, которая называется полюсом плана скоростей, откладываем перпендикулярно ОА отрезок оа, соответствующий скорости точки А.

. Так как для решения задачи будем использовать графический метод, то вводим масштаб скорости:

. Для определения скорости точки В записывается векторное уравнение , связывающее скорости точек А и В , используя теорему о сложении скоростей в переносном и относительных движениях.

Здесь и далее одной чертой подчеркнута скорость известная по направлению, и двумя чертами – скорость, известная по величине и направлению.

Уравнение имеет однозначное решение, если в нем два неизвестных. Поэтому на предварительном этапе необходимо зафиксировать четыре параметра из шести. В данном случае это удается сделать.

Строим план скоростей. Из точки o проводим направление скорости V_B, а из точки а – направление V_BA. Точка пересечения этих линий b определяет величины неизвестных скоростей:

Вопросы для самопроверки

– Что называется зубчатым колесом?

– Назовите основные достоинства и недостатки зубчатых передач?

– Каково взаимное расположение геометрических осей колес в цилиндрических, конических и гиперболоидных передачах?

– Как различаются зубчатые передачи по расположению зубьев относительно образующей тела заготовки колеса?

– Чем отличаются внешнее, внутреннее и реечное зацепления?

– Назовите различие рядовой и планетарной передач?

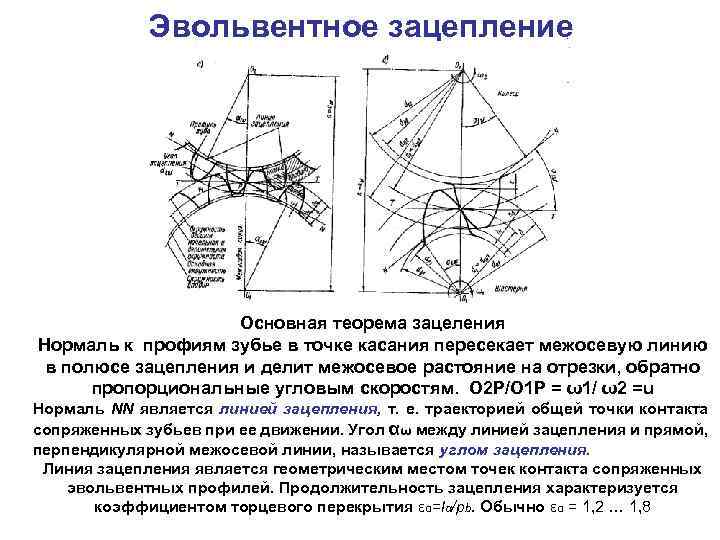
– В чем сущность основной теоремы зубчатого зацепления?

– Назовите элементы зубчатого колеса, какими линиями очерчивается профиль зуба?

– Назовите элементы зацепления пары колес.

– Что называется шагом колеса, модулем, головкой, ножкой зуба?

– Что такое полюс зацепления?

– Какой угол называется углом зацепления?

– Что такое линия зацепления, активная линия зацепления?

– Какая окружность колеса называется начальной окружностью?

– Какая окружность колеса называется основной?

– Какими свойствами обладает делительная окружность?

– Какие зубчатые колеса называются нулевыми, положительными и отрицательными?

– Что является центроидами относительного движения колес при постоянном передаточном отношении?

– Что такое удельное скольжение, почему возникает скольжение в контакте зубъев?

– Почему в полюсе зацепления удельное скольжение равно нулю?

– Происходит ли проскальзывание сопряженных профилей зубьев: в полюсе зацепления, в точках контакта, не совпадающих с полюсом?

– От чего зависит скорость относительного скольжения сопряженных профилей?

– На какой параметр работоспособности передачи влияет величина скорости скольжения?

– Что такое коэффициент удельного давления, где он применяется?

– Какие формы профиля зубьев отвечают основной теореме зубчатого зацепления?

– Дайте определение модуля зацепления.

– Что называется окружным шагом?

– Что такое передаточное число зубчатой передачи?

– Как определить передаточное отношение многоступенчатой зубчатой передачи?

– От чего зависит передаточное отношение рядовой передачи с последовательным соединением колес?

– Какая окружность зубчатого колеса называется делительной?

– Какая часть зуба называется головкой?

– Что такое коэффициент высоты головки зуба, чему он равен?

– Какая часть зуба называется ножкой?

– Могут ли два колеса, находящиеся в зацеплении иметь разный модуль?

– Какая окружность называется окружностью вершин?

– Какая окружность называется окружностью впадин?

– Чему равна высота головки зуба?

– Чему равна высота ножки зуба?

– Каково соотношение между высотой головки и и ножки зуба?

– В каком месте измеряется толщина зуба, ширина впадины колеса?

– Как рассчитать диаметр окружности вершин?

– Как рассчитать диаметр окружности впадин?

– Какая окружность называется эвольвентной?

– Какими свойствами обладает эвольвента окружности?

– Что такое эвольвентная функция?

– Назовите качественные характеристики эвольвентного зацепления?

– Какие профили зубъев колес называются сопряженными?

– Какими методами изготавливают эвольвентные зубъя, в чем заключается существо методов? Каковы основные достоинства и недостатки методов?

– Что такое реечный производящий исходный контур (инструментальная рейка)?

– Что такое коэффициент перекрытия? Каково его минимальное значение, необходимое для нормальной работы передачи?

– Для чего назначаются коэффициенты смещения при нарезании зубчатых колес?

– Какое число зубъев считается минимальным, от чего оно зависит?

– Чем определяется наименьшее число зубьев, обеспечивающее нормальную работу передачи?

– Что такое подрез зубчатого колеса?

– Как предотвратить подрез зубчатого колеса?

– Что такое коэффициент смещения исходного контура?

– Как изменится межосевое расстояние зубчатой передачи, если оба колеса имеют положительную коррекцию?

– Дайте определения окружного и углового шага эвольвентного зацепления.

– Запишите формулу для толщины зуба по окружности произвольного радиуса.

– Какие методы изготовления эвольвентных
зубчатых колес Вы знаете ?

– В чем заключается сущность изготовления эвольвентных колес методом огибания ?

– Выведите основные размеры зубчатого колеса (ra, s,h), используя схему
станочного зацепления.

– Запишите условие отсутствия подрезания в станочном зацеплении.

– Что такое x min ? Выведите формулу для определения x
min.

– Запишите формулу для определения угла зацепления эвольвентной зубчатой передачи.

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Теоретическая механика Сопротивление материалов

Прикладная механика Детали машин
Строительная механика

00:00:00

Геометрический расчет элементов цилиндрической зубчатой передачи

Исходные данные для расчета:

• Модуль m = 4 мм;
• Число зубьев шестерни Z1 = 18;
• Число зубьев колеса Z2 = 30;
• Диаметр вала (ведущий) DB1 = 22 мм;
• Тип шпонки – Призматическая;
• Число шлицев Z – 8;
• Внутренний диаметр шлицев d = 22 мм;
• Диаметр вала (ведомый) DB2 = 30 мм;
• Ширина шлица b = 6 мм;
• Тип – D.

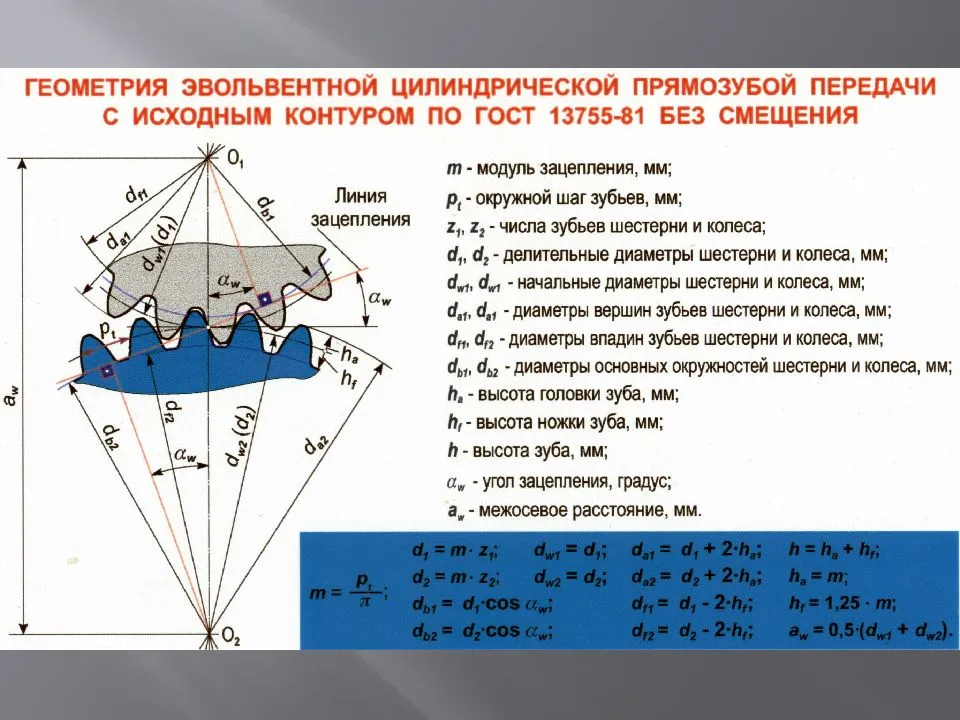
Результаты геометрического расчета цилиндрической зубчатой передачи

• Делительный диаметр шестерни d1=mz1=4×18=72 мм;
• Делительный диаметр колеса d2=mz2=4×30=120 мм;
• Высота головки зуба ha=m =4 мм;
• Высота ножки зуба hf=1,25m=1,25×4=5 мм;
• Высота зуба h=ha+hf=2,25m=2,25×4=9 мм;
• Диаметр вершин зубьев шестерни da1=d1+2ha1=72+2×4=80 мм;
• Диаметр впадин шестерни df1=d1-2hf=72-2×5=62 мм;
• Длина ступицы шестерни Lст1=1,5DB1=1,5×22=33 мм;
• Наружный диаметр ступицы шестерни Dст1=1,6DB1=1,6×22=35,2 мм;
• Диаметр вала шестерни D1=1,2×22=26,4 мм;
• Делительный диаметр колеса d2=mz2=4×30=120 мм;
• Диаметр вершин зубьев колеса da2=d2+2ha=120+2×4=128 мм;
• Диаметр впадин колеса df2=d2-2hf2=120-2×5=110 мм;
• Длина ступицы колеса Lст2=1,5DB2=1,5×30=45 мм;
• Наружный диаметр ступицы колеса Dст2=1,6DB2=1,6×30=48 мм;
• Диаметр вала колеса D2=1,2DB2=1,2×30=36 мм;
• Ширина зубчатого венца b=6m=6×4=24 мм;
• Толщина обода зубчатого венца δ1=2,25m=2,25×4=9 мм;
• Толщина диска δ2=1/3b=8 мм;
• Межосевое расстояние a=0,5(d1+d2)=0,5(72+120)=96 мм;
• Длина шлицев Lшл=(1,5. 2)Lст2=(1,5. 2)45=72 мм.

Достоинства и недостатки

При конструировании механизмов, передающих вращение с высокой нагрузкой, чаще всего останавливаются на выборе шлицевого соединения. Оно имеет в определенных случаях огромные преимущества и может заменить несколько шпоночных соединений. Недостатки также имеются. Надо взвешивать все аргументы за и против, выбирая способ соединения.

В сравнении со шпонками, к достоинствам шлицевых соединений относятся:

• надежность при ударных нагрузках и вибрации;
• возможность уменьшить длину ступицы;
• малые радиальные зазоры;
• увеличение срока эксплуатации;
• отсутствие нагрузки на срез и малая на изгиб благодаря большому пятну контакта;
• несколько линий приложения сил, возможность передавать большие усилия валами с малым диаметром;
• осевое перемещение;
• в соединении только 2 детали;
• компактность;
• точная центровка.

Шлицы изготавливаются по ГОСТ и Стандартам, имеют строго нормализованные размеры и детали для соединения легко подобрать. Упрощена сборка узлов и подгонка деталей.

К недостаткам шлицевых соединений относятся:

• высокая стоимость деталей;
• сложная технология изготовления;
• использование специального оборудования и инструмента.

При перегрузках шпонка просто срезается, не допуская передачи повышенной нагрузки на рабочий механизм и предотвращая его поломку. Деталь простая и дешевая, легко меняется.

В шлицевых соединениях при аварийной ситуации может сломаться зуб или весь станок. Замена деталей сложная и дорогостоящая.

Шлицевое соединение

Использование шлицевого соединения — один из способов жесткой передачи крутящего момента.

Шлицы, по сравнению со шпоночным соединением обладают несколькими преимуществами — лучшей прочностью, точностью и технологичностью.

Шпонки необходимо подгонять, поэтому их рекомендуется применять в единичном или мелкосерийном производстве. Шлицы, в отличае от шпонок, взаимозаменяемы, и рекомендуется использовать в крупносерийном и массовом производстве.

Шлицы считаются более технологичным соединением, чем шпонка, внутренние шлицы изготавливают протягиванием, наружные — фрезерованием (червячными фрезами), долблением, строганием.

В технике применяются прямоугольные, треугольные, трапецеидальные, эвольвентные шлицы.

Наибольшее распространение получили прямоугольные шлицы.

Заключение

Данный курсовой проект по теории машин и механизмов является первой самостоятельной расчетно-графической работой в процессе обучения в университете. Он научил нас самостоятельно решать инженерные задачи, связанные с анализом и синтезом механизмов.

В графической части проекта были спроектированы три механизма: зубчатый механизм, где производилось исследование эвольвентного зацепления зубьев и проектирование зубчатой передачи из условия получения наименьших её габаритов и определение некоторых характеристик этой передачи; шарнирно – рычажный механизм, где производился кинематический и динамический анализ конкретного плоского шарнирно-рычажного механизма и кривошипно-ползунный механизм, для которого были построены графики скорости и ускорения поршня, силы давления на поршень, силы действующей на палец шатуна и моментов, действующих на кривошип.

В расчетно-пояснительной записке был произведен расчет характеристик обоих механизмов. В исследовании эвольвентного зацепления зубьев мы нашли наименьшее число зубьев и определили скорости скольжения зубьев. В исследовании шарнирно-рычажного механизма мы определили скорости, угловые скорости, ускорения, угловые ускорения звеньев механизма и усилия в кинематических парах.

В целом нами была произведена объемная работа, и знания, полученные нами в ходе её выполнения, пригодятся в процессе дальнейшего обучения в университете.

Заключение

Данный курсовой проект по теории машин и механизмов является первой самостоятельной расчетно-графической работой в процессе обучения в университете. Он научил нас самостоятельно решать инженерные задачи, связанные с анализом и синтезом механизмов.

В графической части проекта были спроектированы три механизма: зубчатый механизм, где производилось исследование эвольвентного зацепления зубьев и проектирование зубчатой передачи из условия получения наименьших её габаритов и определение некоторых характеристик этой передачи; шарнирно – рычажный механизм, где производился кинематический и динамический анализ конкретного плоского шарнирно-рычажного механизма и кривошипно-ползунный механизм, для которого были построены графики скорости и ускорения поршня, силы давления на поршень, силы действующей на палец шатуна и моментов, действующих на кривошип.

В расчетно-пояснительной записке был произведен расчет характеристик обоих механизмов. В исследовании эвольвентного зацепления зубьев мы нашли наименьшее число зубьев и определили скорости скольжения зубьев. В исследовании шарнирно-рычажного механизма мы определили скорости, угловые скорости, ускорения, угловые ускорения звеньев механизма и усилия в кинематических парах.

В целом нами была произведена объемная работа, и знания, полученные нами в ходе её выполнения, пригодятся в процессе дальнейшего обучения в университете.

Итоги.

Для того чтобы начертить полный реальный контур зубчатого колеса следует взять координаты точек профиля одного зуба и в любой доступной CAD-программе по этим точкам построить сплайн. Затем нужно размножить его по окружности на количество зубьев, достроить диаметр впадин и получить DXF-чертеж. Имея чертеж, легко написать управляющую программу для станка с ЧПУ и изготовить деталь.

Многие CAD-программы могут выдать чертеж контура зубчатого колеса и без описанных действий, но контур, к сожалению, в большинстве случаев не будет реальным!

Есть интересная программа Gear Template Generator, которая генерирует DXF-файлы контуров зубчатых колес (http://woodgears.ca/gear/index.html). Однако исходные данные для построений какие-то нетрадиционные… да и впадины зубьев — без радиального зазора.

Хочу отметить, что предлагаемый к скачиванию файл Excel с расчетами профиля зуба в данном случае не является полноценной программой и требует от пользователя при работе основополагающих знаний MS Excel и понимания геометрии задачи.

В частности, меняя исходные данные, придется вручную подстраивать шкалы осей и следить за тем, чтобы масштаб по оси X был равен масштабу по оси Y (сетка линий должна образовывать квадратики, а не прямоугольники). Точку сопряжения эвольвенты и переходной кривой при переносе координат в CAD-программу придется корректировать вручную, обрезая ненужные части кривых.

Представленный алгоритм был написан (страшно подумать) в 1992 году для программируемого калькулятора и предназначался для вычерчивания на кульмане чертежей контрольных экранов для оптико-шлифовальных станков.

Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.

Ссылка на скачивание файла с расчетами: profil-zuba (xls 107KB).