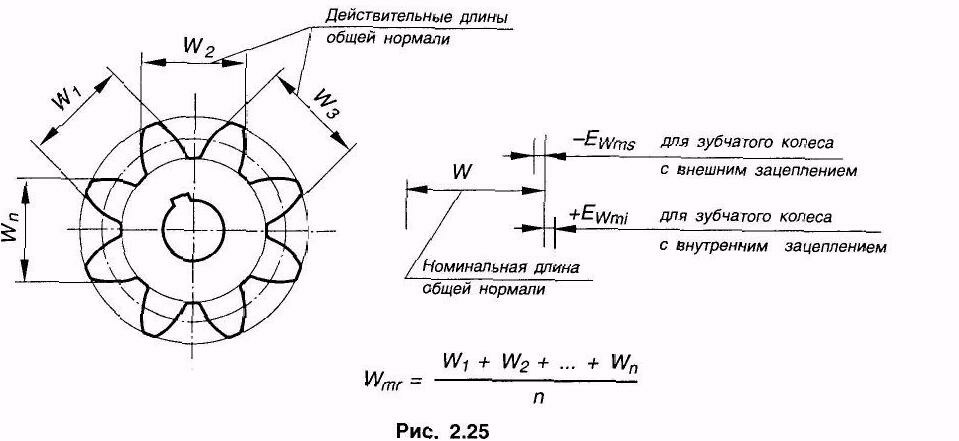
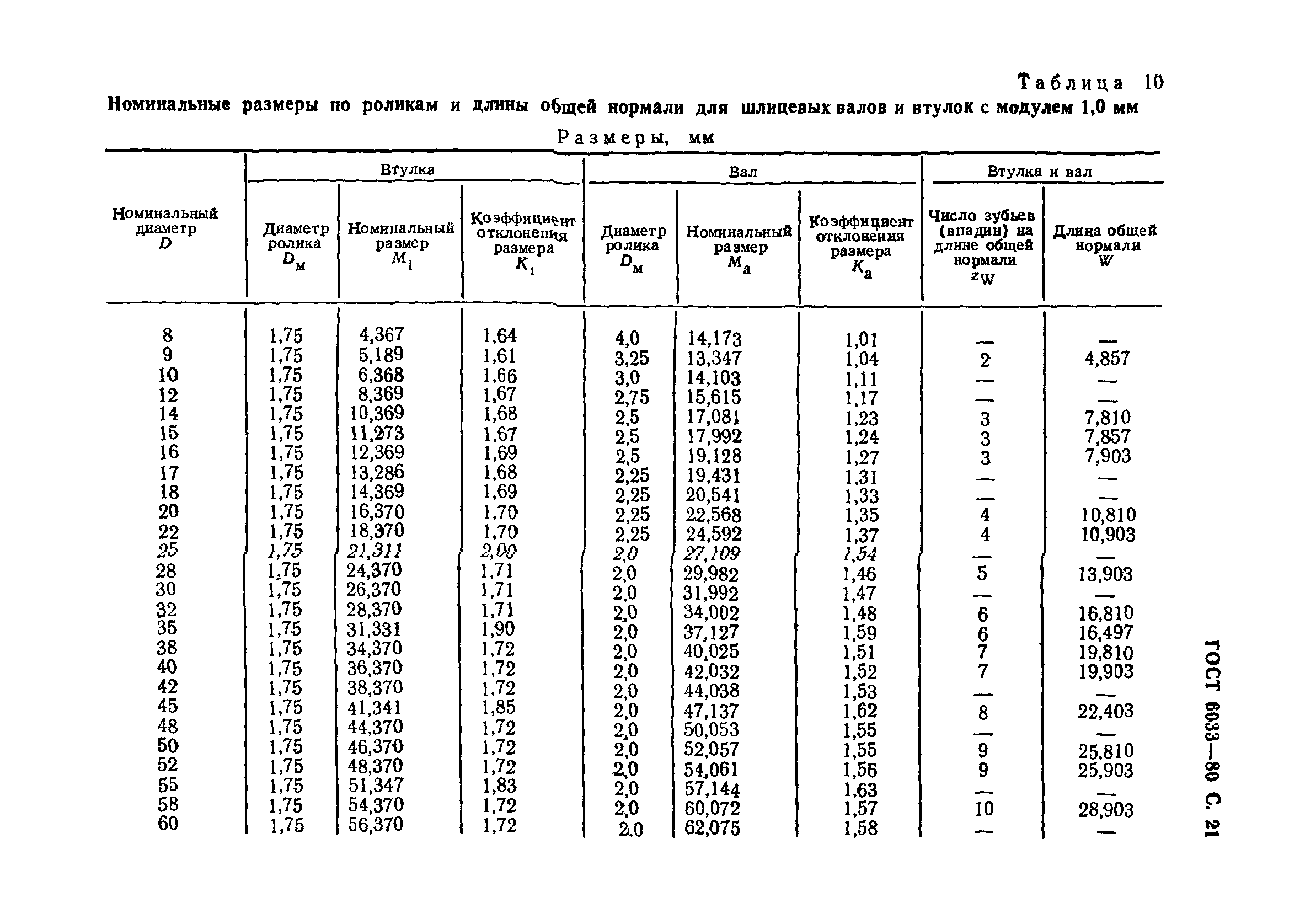
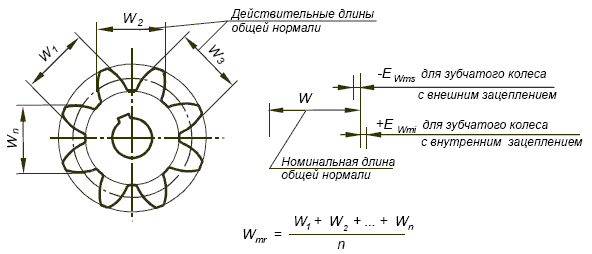
1.3. Допуски на измерительные размеры цилиндрических зубчатых колес
Рассмотренные выше формулы для вычисления номинальных измерительных размеров цилиндрических зубчатых колес гарантируют беззазорное зацепление колес в передаче. В реальных зубчатых передачах должен быть обеспечен гарантированный боковой зазор с целью устранения заклинивания зубьев при работе под нагрузкой в результате температурных деформаций деталей передачи, а также для размещения слоя смазки на рабочих профилях зубьев. Боковой зазор в зацеплении необходим также для компенсации погрешностей изготовления и монтажа передачи. Он определяется в основном величиной межосевого расстояния a w передачи и толщиной s зубьев колес.
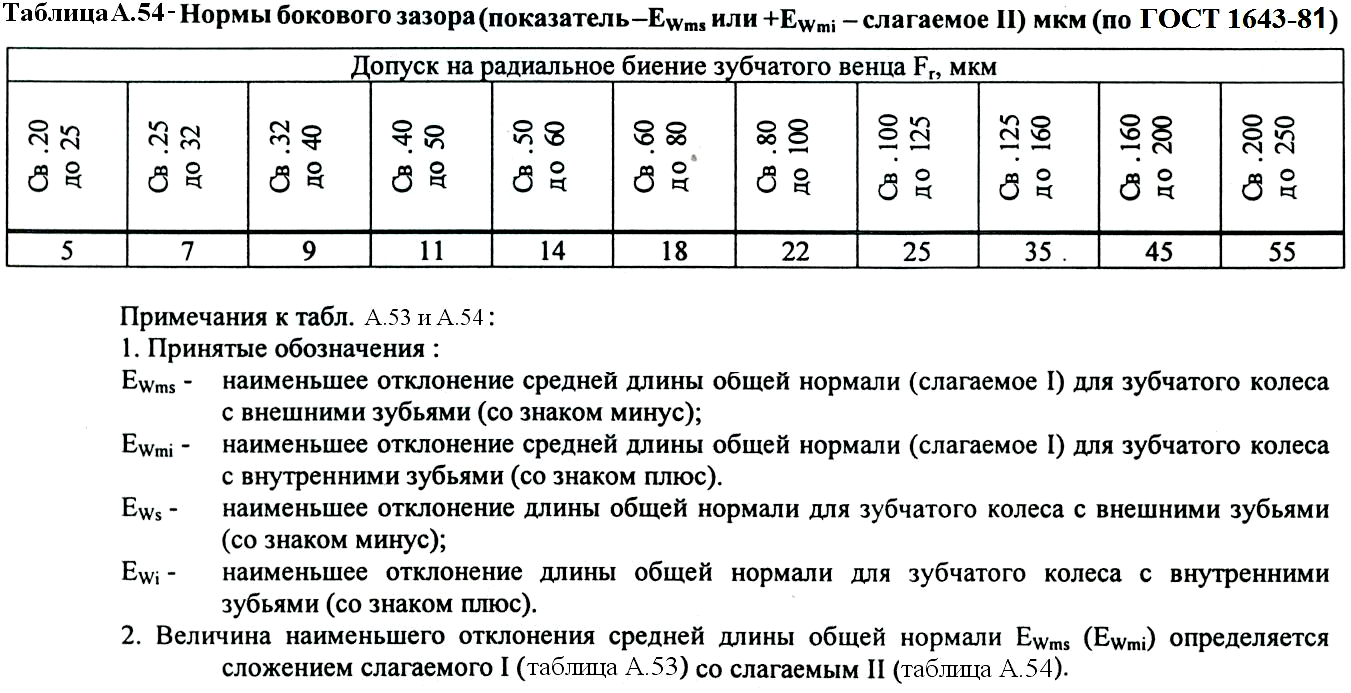
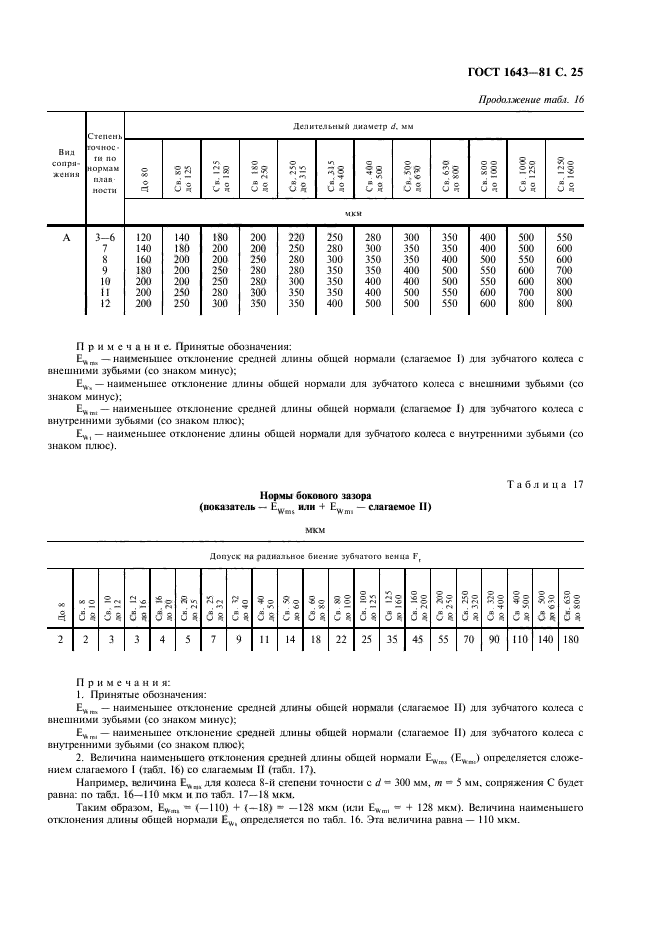
Стандартом на эвольвентные зубчатые цилиндрические передачи (ГОСТ 1643-81) установлено восемь видов допусков на боковой зазор: h, d, c, b, a, z, y, x (обозначения допусков расположены в порядке возрастания величины допуска). Принятая величина гарантированного бокового зазора является основой для назначения вида сопряжения зубчатых колес. Этим же стандартом предусмотрено шесть видов сопряжения: H– нулевой зазор, E – малый зазор, C и D – уменьшенный зазор, B – нормальный зазор, A – увеличенный зазор. Сопряжения видов Н, Е и С требуют повышенной точности изготовления зубьев колес. Их применяют для реверсируемых передач при высоких требованиях к кинематической точности передачи, а также при наличии крутильных колебаний валов передачи. Чаще всего в среднем машиностроении используют передачи с видами сопряжения В и С. При отсутствии специальных требований к зубчатой передаче с каждым видом сопряжения употребляется определенный вид допуска на боковой зазор, обозначаемый строчной буквой, аналогичной букве вида сопряжения (например, А– а, В – в, С – с и т. д.).
Поле допуска на измерительный размер зубчатого колеса всегда направлено в тело зуба, поэтому предельные отклонения измерительного размера (верхнее и нижнее) всегда имеют отрицательные значения .
Модуль шестерни
Шестерни используемые в Slot Car моделях
При конструировании Slot Car (трассовой модели), когда дело доходит до выбора шестерн, то перед нами открывается большой ассортимент на современном рынке с основной величиной модуля 0.3, 0.35 и 0.4. Основными характеристиками шестерни является количество зубьев, модуль шестерни, передаточное число. Если с количеством зубьев и передаточным числом (отношением количества зубьев ведомой к ведущей шестерни) все понятно, то с понятием модуль шестерни не совсем. К сожелению, в школах уже давно не тот уровень преподавания предмета черчения, а в большенстве случаях этот предмент не преподается.
И так, что такое модуль шестерни? Как вычисляется модуль шестерни и чем он обусловен? На этот вопрос нам помог учебник — Техническое черчение, изданный еще в 1972 году (как ни странно, на просторах современного интернета не так уж и много информации по данному вопросу).
Шестерни (на техническом языке — зубчатые колеса) служат для передачи движения от одного элемента машины к другому. Зубчатые колеса в зависимости от характера зацепления (внешнее или внутреннее), взаимного расположения вращающихся валов, способа передачи и т.д. могут быть самой различной конструкции. Наиболее распространенными являются цилиндрические и конические шестерни.
Рисунок 1 — Элементы зубчатого колеса (шестерни)
И так, из каких же элементов состоит шестерня (зубчатое колесо) изображенная на рисунке 1, а. Основным элементом шестерни является зуб (рисунок 1, б) — выступ определенной формы, предназначенный для передачи движения посредством воздействия на выступ другого элемента зубчатой передачи. Часть зубчатого колеса, в которую не входят зубья, называется телом зубчатого колеса (рисунок 1, в). Часть зубчатого колеса, состоящая из всех его зубьев и некоторой связывающей их части тела колеса, называется зубчатым венцом.
Впадиной называется пространство, заключенное между боковыми поверхностями соседних зубьев и поверхностями вершин и оснований впадин (рисунок 1, г).
Начальной поверхностью зубчатого колеса (рисунок 1, д) называется соосная поверхность, по которой катится без скольжения такая же поверхность друого колеа, находящегося в зацеплении с первым. Начальная поверхность колеса делит зуб на две части — головку и ножку.
На рисунке 1, е показано изображение на чертеже некоторых основных элементов зуба. Проекция поверхности выступв на плоскость, перпендикулярную оси зубчатого колеса, называется окружностью выступов, поверхность впадин — окружностью впадин, поверхность делительной поверхности — делительной окружностью. На этом чертеже обозначены высота зуба — h, головки зуба — h’ и ножки зуба — h’‘.
Торцовым шагом t3 называется расстояние по делительной окружности между одноименными профилями смежных зубьев. Диаметр делительной окружности — dд, диаметр окружности выступов — Dе, впадин — Di.
Модулем шестерни m называется отношение диаметра делительной окружности к числу зубьев Z:
Модуль шестерни (зубчатого колеса) можно выразить еще и как отношение торцового шага к числу π:
Высота головки зуба нормального зубчатого колеса примерно равна модулю h’=m, а высота ножки h»≈1,25 m. В соответствии с этими соотношениями можно установить следующую зависимость диаметра выступов De от модуля m и числа зубьев Z зубчатого колеса:
De = m (z + 2).
Рисунок 2 — Условное изображение конического зубчатого колеса (шестерни)
Для передачи движения между валами, оси которых пересекаются, применяются конические зубчатые колеса. Условное изображение конического зубчатого колеса показано на рисунке 2. В разрезе плоскостью, проходящей через ось колеса, зубья изображаются незаштрихованными. На виде, полученном проецированием на плоскость, перпендикулярную оси колеса, сплошными линиями изображаются окружности, соответствующие большому и малому выступу зубьев и штрих-пунктирной линией — окружность большого основания делительного конуса.
У конического зубчатого колеса имеются свои специфические элементы и соответствующие обозначения и размеры, отсутствующие у цилиндрического колеса:
Φ — угол делительного конуса;
Φе — угол конуса выступов;
Φi — угол конуса впадин;
L — конусное расстояние;
ν — угол внешнего дополнительного конуса.
Основные размеры некоррегированных конических зубчатых колес могут быть определены по следующим формулам.
Диаметр начальной окружности:
dд = m z.
Диаметр окружности выступов:
Dе = m (z + 2cos Φ).
Диаметр окружности впадин:
Di = m (z — 2,4cos Φ).
L= dд/(2cos Φ)
По материалам учебника «Техническое черчение» Авторы: Е.И Годик, В.М. Лысянский, В.Е. Михайленко, А.М. Пономарев. Киев. 1972г
§ 5. ЗУБЧАТЫЕ ПЕРЕДАЧИ.
Раздел: БИБЛИОТЕКА ТЕХНИЧЕСКОЙ ЛИТЕРАТУРЫ Короткий путь https://bibt.ru <<�Предыдущая страница Оглавление книги Следующая страница>>
Зубчатые передачи широко применяют в транспортных, сельскохозяйственных машинах и в промышленном оборудовании. С их помощью изменяют по величине и направлению скорости движущихся частей станков и передают от одного вала к другому усилия и крутящие моменты. Крутящий момент равен произведению силы на плечо, кГм.
Рис. 116. Основные элементы зубчатого колеса
Элементы зубчатого колеса.
В каждом зубчатом колесе (рис. 116) различают три окружности: делительную окружность, окружность выступов, окружность впадин, а следовательно, три соответствующих им диаметра.
Делительная, или начальная окружность зубчатого колеса делит зуб по высоте на две неравные части: верхнюю, называемую головкой зуба, и нижнюю, называемую ножкой зуба. Высоту головки обозначают h’, а высоту ножки h». Диаметр этой окружности обозначается Dд.
Окружность выступов зубчатого колеса — это окружность, ограничивающая сверху профили зубьев колеса. Обозначают ее De.
Окружность впадин зубчатого колеса проходит по основанию впадин зубьев и обозначается Di.
Расстояние между серединами двух соседних зубьев, измеренное по дуге делительной окружности, называется шагом зубчатого зацепления и обозначается буквой t.
Величина элемента зубчатого колеса задается в долях модуля (m). Модуль показывает долю диаметра начальной окружности в миллиметрах, приходящуюся на один зуб, т. е,
Dд/z=m,
где z — число зубьев зубчатого колеса.
Если шаг, выраженный в миллиметрах, разделить на число π=3,14, то также получим модуль, т. е. m=t/π мм, а тогда шаг будет t=mπ.
Дуга делительной окружности S в пределах зуба называется толщиной зуба зубчатого колеса, дуга S’ — шириной впадин. Размер b зуба по линии, параллельной оси колес, называется длиной зуба.
Радиальный зазор δ (см. рис. 118,б)-кратчайшее расстояние между вершиной зуба и основанием впадины сопряженного колеса.
Боковой зазор зубчатого колеса Сп (см. рис. 118, б)-кратчайшее расстояние между нерабочими профильными поверхностями смежных зубьев, когда их рабочие поверхности находятся в контакте.
С модулем связаны все элементы зубчатого колеса:
высота головки зуба h’ = m;
высота ножки зуба h» =1,25 m;
высота всего зуба h= h’+h»=m+1,25m = 2,25m.
Зная число зубьев z, с помощью модуля можно определить диаметр делительной окружности зубчатого колеса.
Dд=mz.
Диаметр окружности выступов (диаметр заготовки зубчатого колеса) вычисляют по формуле:
De=Dд+2h’=zm+2m=(z+2)m.
Формулы, с помощью которых можно определить параметры цилиндрических зубчатых колес в зависимости от модуля и числа зубьев z, приведены в табл. 8.
Таблица 8 Формулы для расчета параметров цилиндрических зубчатых колес
| Формулы | ||
| Наружный диаметр | De | (z+2)m; Dд+2m; (z2+2)(t/π) |
| Диаметр начальной окружности | Dд | mz; De-2m |
| Модуль | m | t/π; Dд/z; De/(z+2) |
| Шаг зацепления | t | mπ; (πDд)/z |
| Высота зуба (глубина впадины) | h | 2,25m; h’+h» |
| Высота головки зуба | h’ | m; t/π |
| Высота ножки зуба | h» | 1,25m; h-h’ |
| Измеренные по начальной окружности: Толщина зуба | S | t/2; (πm)/2 |
| Измеренные по начальной окружности: Ширина впадины | S’ | t/2; (πm)/2 |
| Межцентровое расстояние | A | ((z1+z2)/2)m |
| Радиальный зазор | δ | 0,25m; h»-h’ |
Для зубчатых колес применяются углеродистые и легированные стали с содержанием углерода от 0,2 до 0,6%.
Для литых колес применяют литейные стали марок 35Л, 50Л, а также легированные литейные стали — 40ХЛ, 30ХГСЛ, 40ХНЛ и др.
Для изготовления зубчатых колес применяют серый чугун марок СЧ 28-48; СЧ 32-52; СЧ 35-56 и модифицированный чугун МСЧ 32-52 и МСЧ 35-56.
Из неметаллических материалов для изготовления одного из зубчатых колес пары применяют текстолит, лигнофоль, нейлон, искусственную кожу и фибру. Второе колесо выполняют из стали или чугуна с твердостью рабочей поверхности не более НВ 250.
Перейти вверх к навигации
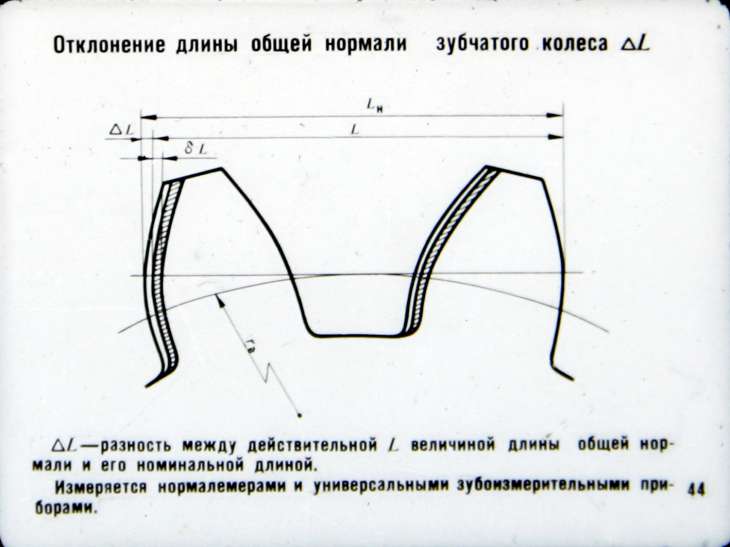
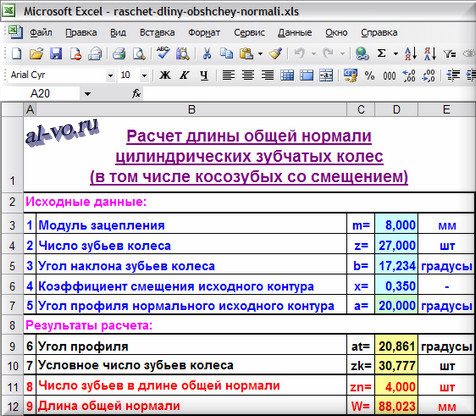
Колебание – длина – общая нормаль
Колебание длины общей нормали ( Д0Ь) определяется разностью между наибольшей и наименьшей длиной общей нормали, полученной при измерении ее по всей окружности проверяемого зубчатого колеса. Колебание длины общей нормали ( по окружности колеса) определяют как разность между наибольшей и наименьшей длиной нормали (
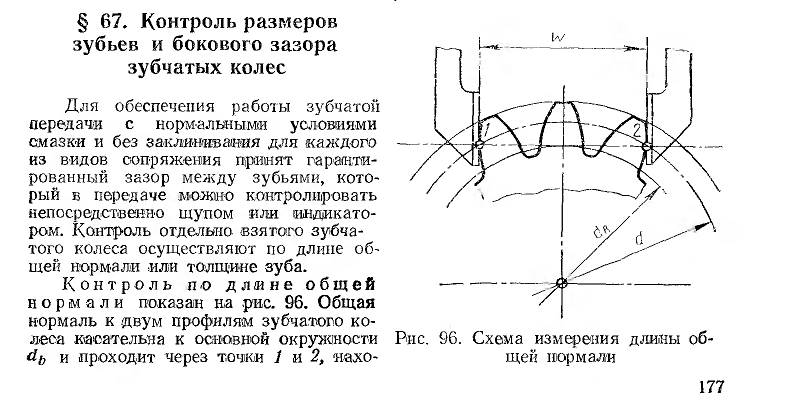
Колебание длины общей нормали L контролируют на приборах, имеющих два наконечника с параллельными плоскостями и в за-ьиеимости от требуемой точности отсчетное нониусное, микрометрическое 2 или индикаторное устройство. Особенностью контроля длины общей нормали является отсутствие необходимости базирования колеса по его оси.
Колебание длины общей нормали L контролируют на приборах, имеющих два наконечника о параллельными плоскостями и в зависимости от требуемой точности отсчетное нониусное, микрометрическое 2 или индикаторное устройство. Особенностью контроля длины общей нормали является отсутствие необходимости базирования колеса по его оси.
Колебание длины общей нормали Va r можно контролировать разным инструментом, у которого имеются две параллельные измерительные плоскости.
Колебание длины общей нормали F находят как разность между наибольшей и наименьшей действительными длинами общей нормали при последовательном измерении всех групп зубьев проверяемого колеса. Колебание длины общей нормали может быть показателем погрешности обката при зубообразовании.
| Кривая накопленной погрешности шага. |
Колебанием длины общей нормали FVWr называется расстояние между двумя параллельными плоскостями касательными к двум разноименным активным боковым поверхностям зубьев зубчатого колеса.
На колебание длины общей нормали влияют лишь тангенциальные составляющие погрешности окружных шагов и не влияют радиальные. Поэтому для полной оценки колеса в отношении кинематической точности необходимо проконтролировать колесо и по одному из параметров, учитывающих радиальные составляющие погрешностей окружных шагов, например измерить радиальное биение.
| Кривая накопленной погрешности шага. |
Измерение колебания длины общей нормали проводится любым прибором, имеющим измерительные поверхности в виде параллельных плоскостей, например штангенциркулями.
Контроль колебания длины общей нормали производится на станковых приборах, имеющих специальные приспособления, или накладными – нормалемерами и микрометрическими скобами для зубчатых колес.
Величина колебания длины общей нормали 1UL определяется как разность наибольшей и наименьшей длины общей нормали при последовательном измерении всех групп зубьев по окружности колеса. В этом случае настройки по блоку плиток не требуется.
Контроль колебания длины общей нормали прост и не требует иметь какой-либо промежуточной измерительной базы. Часто производится измерение длины общей нормали, а не ее колебания. Это осуществляется с целью выяснения толщины зуба и рассматривается ниже.
Контроль колебания длины общей нормали может осуществляться с помощью микрометров ( фиг. Кирове ( КРИН), у которых в отличие от обычного микрометра имеются тарельчатые измерительные поверхности. Недостатком микрометров является то, что одна измерительная поверхность вращается и при соприкосновении с контролируемой поверхностью несколько увлекает весь прибор. Для контроля колебаний длины общей нормали более удобен прибор конструкции завода ЛИЗ ( фиг. Для колес средних размеров контроль колебания длины общей нормали удобно производить с помощью индикаторных скоб ( фиг.
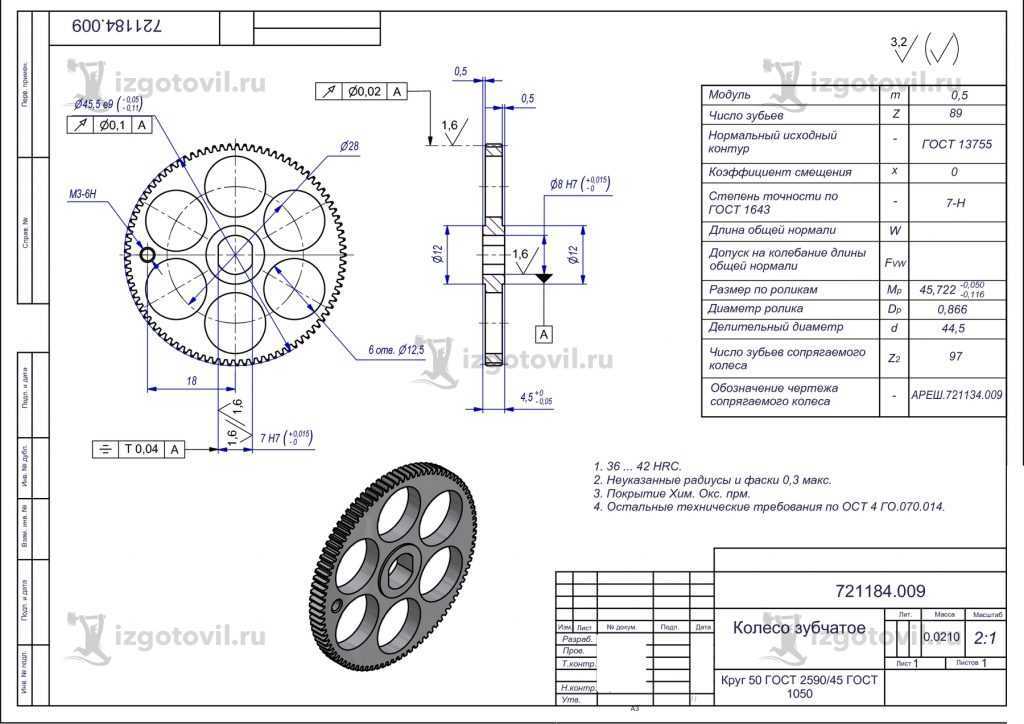
Конструкция зубчатого колеса
Несмотря на кажущуюся простоту, в технике принято выделять несколько отдельных частей зубчатого колеса. Как и любое другое колесо, зубчатый вариант в своей основе имеет диск необходимого диаметра. Основной частью является обод, на боковой или торцевой поверхности которого выполнены зубья. Все вместе они образуют так называемый венец зубчатого колеса. Геометрия зубьев различна у разных типов зубчатой передачи. Сам зуб условно разбивается на несколько частей. Наружная часть называется вершиной. Прилегающие к ней боковые поверхности носят название головки зуба. Внутренняя часть именуется ножкой зуба. Две соседние ножки образуют впадину зубчатого колеса.
Для крепления на валу механизма в центре диска изготавливается ступица со сквозным отверстием. Форма отверстия зависит от геометрии сечения вала и может быть цилиндрической, квадратной или многоугольной. При использовании цилиндрических валов, в ступице обычно выполняют шпоночный паз.
С целью уменьшения веса толщина диска колеса выполняется обычно меньше, чем толщина ступицы или обода. Также для этого в теле диска могут присутствовать окна разнообразной формы.
Основные параметры зубчатых цилиндрических передач
Стандарт распространяется на цилиндрические передачи внешнего зацепления для редукторов и ускорителей, в том числе и комбинированных (коническо-цилиндрических, цилиндро-червячных и др.), выполняемых в виде самостоятельных агрегатов. Стандарт не распространяется на передачи редукторов специального назначения и специальной конструкции Для встроенных передач стандарт является рекомендуемым
Межосевые расстояния
| 1 ряд | 40 | 50 | 63 | 80 | 100 | 125 | — | 160 | — | 200 | — | 250 | — | 315 | — | 400 |
| 2 ряд | — | — | — | — | — | — | 140 | — | 180 | — | 225 | — | 280 | — | 355 | — |
| 1 ряд | — | 500 | — | 630 | — | 800 | — | 1000 | — | 1250 | — | 1600 | — | 2000 | — | 2500 |
| 2 ряд | 450 | — | 560 | — | 710 | — | 900 | — | 1120 | — | 1400 | — | 1800 | — | 2240 | — |
1-й ряд следует предпочитать 2-му
Номинальные передаточные числа
| 1 ряд | 1,0 | — | 1,25 | — | 1,6 | — | 2,0 | — | 2,5 | — | 3,15 | |
| 2 ряд | — | 1,12 | — | 1,4 | — | 1,8 | — | 2,24 | — | 2,8 | — | |
| 1 ряд | — | 4,0 | — | 5,0 | — | 6,3 | — | 8,0 | — | 10 | — | 12,5 |
| 2 ряд | 3,55 | — | 4,5 | — | 5,6 | — | 7,1 | — | 9,0 | — | 11,2 | — |
1-й ряд следует предпочитать 2-му Фактические значения передаточных чисел не должны отличаться от номинальных более чем на 2,5% при номинальном меньше 4,5 и на 4% при номинальном больше 4,5
Коэффициент ширины зубчатых колес (отношение ширины зубчатого колеса к межосевому расстоянию) должен соответствовать: 0,100; 0,125; 0,160; 0,200; 0,315; 0,400; 0,500; 0,630; 0,800; 1,0; 1,25
Численные значения ширины зубчатых колес округляются до ближайшего числа из ряда Ra20 по ГОСТу 6636
При различной ширине сопряженных зубчатых колес значение коэффициента ширины зубчатых колес относится к более узкому из них
Коэффициент запаса прочности при работе зуба двумя сторонами
например: зубья реверсивных передач или зубья сателлитов в планетарных передачах
| Материал колес и термо- обработка | Отливки стальные и чугунные без термо- обработки | Отливки стальные и чугунные с термо- обработкой | Поковки стальные нормали- зованные или улучшенные | Поковки и отливки стальные с поверх- ностной закалкой (сердцевина вязкая) | Стальные, нормали- зованные или улучшенные, а также с поверх- ностной закалкой | Стальные с объемной закалкой | Стальные, подверг- нутые цементации, азоти- рованию, циани- рованию и др. | Чугунные и пласт- массовые колеса |
| Коэфф. | 1,9 | 1,7 | 1,5 | 2,2 | 1,4 — 1,6 | 1,8 | 1,2 | 1 — 1,2 |
Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 | 1800 | 2000 | 2240 | 2500 |
Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 |
| Промежуточная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 100 | 125 | 160 | 200 | 250 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 | 560 | 630 |
| Промежуточная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
Применение
Высокие свойства зубчатых передач нашли отражение в широком спектре применений. Во многих промышленных механизмах используются редукторы, призванные понизить число оборотов вращения вала двигателя, для передачи на технологическое оборудование. Помимо изменения скорости, такое устройство также увеличивает механический момент. В итоге маломощный двигатель с большой скоростью вращения, способен приводить в движение медленный и тяжелый механизм.
С целью уменьшения габаритов редуктора его часто выполняют многоступенчатым. Большое количество зубчатых колес входят в последовательное зацепление между собой, обеспечивая высокое передаточное число. Классическим примером подобного устройства являются обычные механические часы. Благодаря множеству специально подобранных передач, скорости движения секундной, минутной и часовой стрелок отличаются друг от друга ровно в 60 раз.
Меняя один комплект на другой, можно получить разные скорости выходного вала. Этот принцип действия лег в основу коробок переключения передач, широко используемых в автомобилестроении, станкостроении и других отраслях.
Обычное зубчатое колесо допускает применение и для повышения скорости выходного вала относительно входного. В общем случае для этого достаточно развернуть редуктор или поменять местами точки подключения двигателя и конечного механизма. Называется подобное устройство мультипликатор. Из особенностей его применения необходимо учитывать запас по мощности двигателя, сопоставимый с передаточным числом механизма.
Зубчатые колеса используются также для изменения направления движения. Две цилиндрические шестерни с одинаковым числом зубьев реализуют функцию смены направления вращения вала. Передачи конической или корончатой конструкции используются в случае необходимости смены положения оси в пространстве. Ведущая и ведомая шестерни в таких механизмах развернуты друг относительно друга на какой-либо угол, значение которого может достигать 90 градусов. При этом передаточное отношение часто равно единице, что обеспечивает одинаковые скорости валов.
Наряду с простыми вариантами передач, содержащих зубчатые колеса, разработаны несколько специальных моделей. С целью снижения материалоемкости, в механизмах с ограниченным углом поворота, используют только часть зубчатого колеса. Такой сектор, обладая всеми основными свойствами зубчатого зацепления, отличается более низкой массой и стоимостью.
Еще один вариант, называемый планетарной передачей, также характеризуется малым весом и габаритами. При этом устройство обеспечивает высокое значение передаточного числа и пониженный уровень шума в процессе работы. Конструктивно такая передача состоит из нескольких шестерен, имеющих разную степень свободы. За счет этого механизм может не только передавать вращение, но и складывать или выделять угловые скорости разных валов, находящихся на одной оси. Сегодня разработано большое число вариантов планетарных передач, отличающихся типом и взаимным расположением зубчатых колес. Планетарные передачи широко применяются в автомобильной и авиационной технике, тяжелом металлорежущем оборудовании. Среди недостатков, сдерживающих распространение передач данного типа, следует отметить низкий КПД и высокие конструктивные требования к точности изготовления отдельных деталей.
Важные замечания
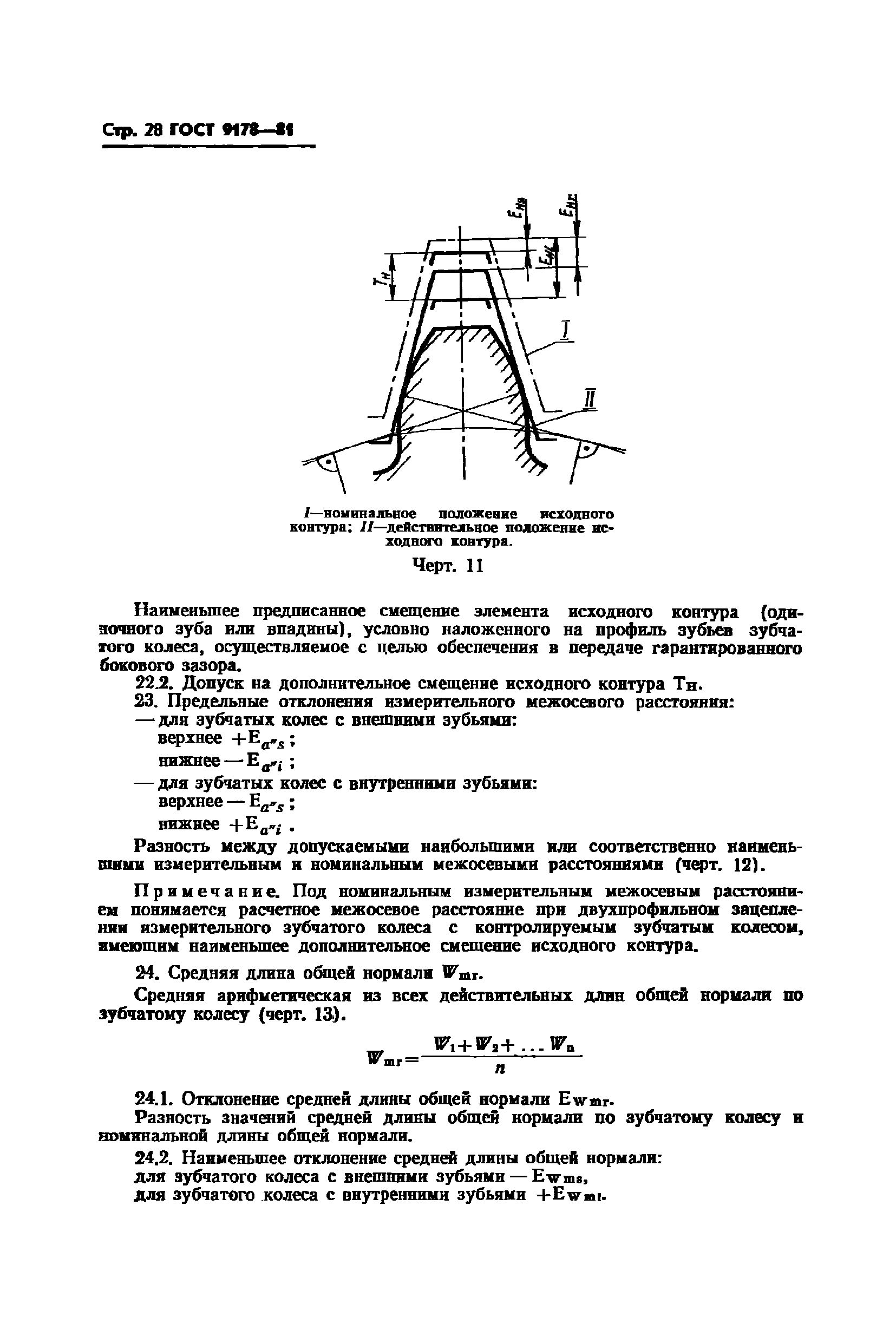
Смещение исходного контура при нарезке зубьев применяют для восстановления изношенных поверхностей зубьев колеса, уменьшения глубины врезания на валах-шестернях, для увеличения нагрузочной способности зубчатой передачи, для выполнения передачи с заданным межосевым расстоянием не равным делительному расстоянию, для устранения подрезания ножек зубьев шестерни и головок зубьев колеса с внутренними зубьями.
Различают высотную коррекцию (xΣ(d)=) и угловую (xΣ(d)≠).
Смещение производящего контура на практике применяют обычно при изготовлении прямозубых колес и очень редко косозубых. Это обусловлено тем, что по изгибной прочности косой зуб прочнее прямого, а необходимое межосевое расстояние можно обеспечить соответствующим углом наклона зубьев. Если высотную коррекцию изредка применяют для косозубых передач, то угловую практически никогда.
Косозубая передача работает более плавно и бесшумно, чем прямозубая. Как уже было сказано, косые зубья имеют более высокую прочность на изгиб и заданное межосевое расстояние можно обеспечить углом наклона зубьев и не прибегать к смещению производящего контура. Однако в передачах с косыми зубьями появляются дополнительные осевые нагрузки на подшипники валов, а диаметры колес имеют больший размер, чем прямозубые при том же числе зубьев и модуле. Косозубые колеса менее технологичны в изготовлении, особенно колеса с внутренними зубьями.
Подписывайтесь на анонсы статей в окнах, расположенных в конце каждой статьи или вверху каждой страницы.
Прошу уважающих труд автора скачивать файл после подписки на анонсы статей!
Ссылка на скачивание файла: modul-zubchatogo-kolesa (xls 41,0KB).
Другие статьи автора блога
На главную