Деформация растяжения-сжатия

Формулы и способы расчета пружин из стали круглого сечения по ГОСТ 13765

Пружина сжатия                                                                                                                           Пружина растяжения

Наименование параметра	Обозначение	Расчетные формулы и значения
Сила пружины при предварительной деформации, Н	F 1	Принимается в зависимости от нагрузки пружины
Сила пружины при рабочей деформации (соответствует наибольшему принудительному перемещению подвижного звена в механизме), Н	F 3	Принимается в зависимости от нагрузки пружины
Рабочий ход пружины, мм	h	Принимается в зависимости от нагрузки пружины
Наибольшая скорость перемещения подвижного конца пружины при нагружении или разгрузке, м/с	v max	Принимается в зависимости от нагрузки пружины
Выносливость пружины, число циклов до разрушения	N F	Принимается в зависимости от нагрузки пружины
Наружный диаметр пружины, мм	D 1	Предварительно принимаются с учетом конструкции узла. Уточняются по таблицам ГОСТ 13766…ГОСТ 13776
Относительный инерционный зазор пружины сжатия. Для пружин растяжения служит ограничением максимальной деформации	δ	δ = 1 — F 2 / F 3 (1) Для пружин сжатия классов I и II δ = 0,05 — 0,25 для пружин растяжения δ = 0,05 — 0,10 для одножильных пружин класса III δ = 0,10 — 0,40 для трехжильных класса III δ = 0,15 — 0,40
Сила пружины при максимальной деформации, Н	F 3	Уточняется по таблицам ГОСТ 13766 ÷ ГОСТ 13776
Сила предварительного напряжения (при навивке из холоднотянутой и термообработанной проволоки), Н	F	(0,1 ÷ 0,25) F 3
Диаметр проволоки, мм	d	Выбирается по таблицам ГОСТ 13764 ÷ ГОСТ 13776
Диаметр трехжильного троса, мм	d 1	Выбирается по таблицам ГОСТ 13764 ÷ ГОСТ 13776
Жесткость одного витка пружины, Н/мм	c 1	Выбирается по таблицам ГОСТ 13764 ÷ ГОСТ 13776
Максимальная деформация одного витка пружины, мм	s’ (при F = 0) s» (при F > 0)	Выбирается по таблицам ГОСТ 13764 ÷ ГОСТ 13776
Максимальное касательное напряжение пружины, МПа	τ 3	Для трехжильных пружин
Критическая скорость пружины сжатия, м/с	v k	Для трехжильных пружин
Модуль сдвига, МПа	G	Для пружинной сталиG = 7,85 х 104
Динамическая (гравитационная) плотность материала, Н • с2/м4	ρ	ρ = γ / g, где g — ускорение свободного падения, м/с2 γ — удельный вес, Н/м3 Для пружинной стали ρ = 8•103
Жесткость пружины, Н/мм	с	Для пружин с предварительным напряжением Для трехжильных пружин
Число рабочих витков пружины	n
Полное число витков пружины	n 1	где n2 — число опорных витков
Средний диаметр пружины, мм	D	Для трехжильных пружин
Индекс пружины	i	Для трехжильных пружин Рекомендуется назначать от 4 до 12
Коэффициент расплющивания троса в трехжильной пружине, учитывающий увеличение сечения витка вдоль оси пружины после навивки	Δ	Для трехжильного троса с углом свивки β = 24° определяется по таблице i 4,0 4,5 5,0 5,5 6,0 7,0 и более Δ 1,029 1,021 1,015 1,010 1,005 1,000
Предварительная деформация пружины, мм	s 1
Рабочая деформация пружины, мм	s 2
Максимальная деформация пружины, мм	s 3
Длина пружины при максимальной деформации, мм	l 3	где n3 — число обработанных витков Для трехжильных пружин Для пружин растяжения с зацепами
Длина пружины в свободном состоянии, мм	l
Длина пружины растяжения без зацепов в свободном состоянии, мм	l’
Длина пружины при предварительной деформации, мм	l 1	Для пружин растяжения
Длина пружины при рабочей деформации, мм	l 2	Для пружин растяжения
Шаг пружины в свободном состоянии, мм	t	Для трехжильных пружин Для пружин растяжения
Напряжение в пружине при предварительной деформации, МПа	τ 1
Напряжение в пружине при рабочей деформации, МПа	τ 2
Коэффициент, учитывающий кривизну витка пружины	k	Для трехжильных пружин
Длина развернутой пружины (для пружин растяжения без зацепов), мм	l
Масса пружины (для пружин растяжения без зацепов), кг	m
Объем, занимаемый пружиной (без учета зацепов пружины), мм 3	V
Зазор между концом опорного витка и соседним рабочим витком пружины сжатия, мм	λ	Устанавливается в зависимости от формы опорного витка
Внутренний диаметр пружины, мм	D 2
Временное сопротивление проволоки при растяжении, МПа	R m	Устанавливается при испытаниях проволоки или по ГОСТ 9389  и ГОСТ 1071
Максимальная энергия, накапливаемая пружиной, или работа деформации, мДж		Для пружин сжатия и растяжения без предварительного напряжения Для пружин растяжения с предварительным напряжением

Напряжения при растяжении сжатии

Применяя гипотезу Бернулли для продольной упругой деформации стержня, можно определить продольную силу N как равнодействующую всех рассредоточенных по сечению внутренних усилий. Догадка Бернулли одновременно с гипотезой о ненадавливании волокон позволяет сказать, что ? в произвольной точке разреза будут постоянны, т.к. реакция продольных волокон одинакова на всем поперечном разрезе. Для определения величины нормального напряжения ? применяется следующая формула:

Напряжение для упруго деформированного стержня описывается как отношение внутренней силы N к площади сечения A. Считается позитивным при растяжении, при сжатии рассматривается как отрицательное.

Безоговорочная дефармация зависит от жесткости сечения, величины продольной силы и длины бруса. Зависимость можно описать по следующей формуле:

Аналогичным образом, методика расчета величины полного изменения длины такая: нужно высчитать отношение значения продольной силы N помноженной на длину стержня l и жесткости сечения (творение модуля Юнга E на площадь сечения A).

В настоящих расчетах на брус действует очень много разнонаправленных сил, с целью решения этих задач требуется построение эпюр, которые могут воочию показать какие напряжения работают на различных участках, чем вызвана дефармация при растяжении и сжатии.

В рамках такой квазистатической (условно статической) системы, как брус или стержень с переменным сечением или отверстием, вероятная энергия растяжения может быть рассмотрена как сумма энергий гомогенных участков

При проведении расчетов важно правильно поделить стержень на участки и создать все участвующие в процессе силы и напряжения. Для настоящих расчетов построение эпюр – непосильная задача, которая просит от инженера отличного понимания действующих на деталь нагрузок

К примеру, вал со шкивами разнообразного диаметра просит в первую очередь определения критических точек и разбивки на необходимые участки, после построения графиков по ним.

Деформация изгиба

Рассмотрим примеры деформации данного вида. В случае изгиба, выпуклая часть тела подвергается некоторому растяжению, а вогнутый фрагмент сжимается. Внутри тела, подвергающегося данному варианту деформации, есть слой, который не испытывает ни сжатия, ни растяжения. Его принято называть нейтральным участком деформируемого тела. Вблизи него можно уменьшить площадь тела.

В технике примеры деформации данного типа используют для экономии материалов, а также для уменьшения веса возводимых конструкций. Сплошные брусья и стержни заменяют трубами, рельсами, двутавровыми балками.

Испытание на сжатие:

Испытание на сжатие – это определение поведения материала при сжимающей нагрузке.

Испытание на сжатие обычно используется для камня и бетона. Испытание на сжатие показывает напряжение и деформацию материала. Экспериментальный результат должен подтвердить теоретические выводы.

Виды компрессионного тестирования: 

• Испытание на изгиб
• Весенний тест
• Испытание на раздавливание

Испытание на сжатие предназначено для определения параметров целостности и безопасности материала путем выдерживания сжимающего напряжения. Также обеспечивается сохранность готовой продукции, комплектующих, изготавливаемого инструмента. Он определяет, подходит ли материал для этой цели и соответствующим образом изготовлен.

Тесты сжатия предоставляют данные для следующих целей:

• Для измерения качества партии
• Чтобы понять последовательность в производстве
• Помочь в процедуре проектирования
• Уменьшить цену материала
• Гарантировать качество по международным стандартам и т. Д.

Напряжения при растяжении-сжатии.

Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:

где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.

Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

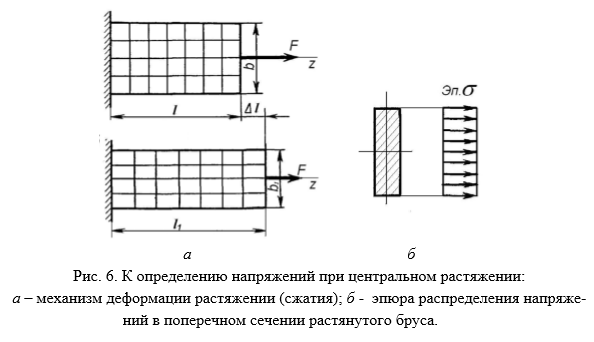
Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:

Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.

для углеродистых и низколегированных сталей

Ст3, 09Г2С, 16ГС, 20, 20К, 10, 10Г2, 09Г2, 17ГС, 17Г1С, 10Г2С1:

1. При расчетных температурах ниже 20°С допускаемые напряжения принимают такими же, как и при 20°С, при условии допустимого применения материала при данной температуре.
2. Для промежуточных расчетных температур стенки допускаемое напряжение определяют линейной интерполяцией с округлением результатов до 0,5 МПа в сторону меньшего значения.
3. Для стали марки 20 при Re/20e/20 / 220.
4. Для стали марки 10Г2 при Rр0,2/20р0,2/20 / 270.
5. Для стали марок 09Г2С, 16ГС классов прочности 265 и 296 по ГОСТ 19281 допускаемые напряжения независимо от толщины листа определяют для толщины свыше 32 мм.
6. Допускаемые напряжения, расположенные ниже горизонтальной черты, действительны при ресурсе не более 105 ч. Для расчетного срока эксплуатации до 2*105 ч допускаемое напряжение, расположенное ниже горизонтальной черты, умножают на коэффициент: для углеродистой стали на 0,8; для марганцовистой стали на 0,85 при температуре < 450 °С и на 0,8 при температуре от 450 °С до 500 °С включительно.

Примеры деформации разных видов

1. Играем на гитаре — кратковременно растягиваем струны

2. Садимся в автомобиль — пружины подвески сжимаются

3. Сидим на тонкой доске — доска прогибается

4. Затягиваем шуруп — происходит кручение отвёртки (хоть мы и не видим деформацию отвёртки)

5. Двигаем расшатанный стул — происходит сдвиг сиденья относительно пола

{"questions":,"explanations":,"answer":}},"hints":},{"content":"Какому виду деформации подвергается мяч при ударе?`choice-7`","widgets":{"choice-7":{"type":"choice","options":,"explanations":,"answer":}},"hints":},{"content":"Упругую дощечку сломали пополам. Какой вид деформации произошёл?`choice-16`","widgets":{"choice-16":{"type":"choice","options":,"explanations":,"answer":}},"hints":}]}

Деформации при растяжении сжатии

При растяжении/сжатии бруса могут возникать 2 вида деформации. Первый – упругая, второй – пластическая. Для упругой деформации характерно восстановление первоначальных параметров после прекращения воздействия. В случае пластической стадии деформации материала он утрачивает и не восстанавливает форму и размеры. Величина воздействия для перехода одного вида в другой называется пределом текучести.

Для расчета перемещения при растяжении бруса или стержня следует использовать метод разделения на участки, в рамках которых осуществляется приложение внешних воздействий. В точках воздействия силы следует вычислить величину изменения длины, используя формулу: Δl=Nl/EA. Как видно она зависит от жесткости сечения, длины бруса или стержня и величины действующей продольной силы. Итоговым перемещением для бруса целиком будет сумма всех частичных перемещений, рассчитанных для точек приложения силы.

Поперечные деформации бруса (становится более толстым при сжатии и тонким при растяжении) также характеризуются абсолютной и относительной величиной деформации. Первая – разность между размером сечения после и до приложения внешних воздействий, вторая – отношение абсолютной деформации к его исходному размеру. Коэффициент Пуассона, отражающий линейную зависимость продольной и поперечной деформаций, определяет упругие качества материалов и считается неизменным для растяжения и сжатия. Продольные наиболее наглядно отражают процессы, происходящие в брусе или стержне при внешнем воздействии. Зная величину любой из них (продольной или поперечной) и используя коэффициент Пуассона, можно рассчитать значение неизвестной.

Для определения величины деформации пружины при растяжении можно применить закон Гука для пружин:

F=kx

В данном случае х – увеличение длины пружины, k – коэффициент жесткости (единица измерения Н/м), F – сила упругости, направленная в противоположную от смещения сторону. Величина абсолютной деформации будет равна отношению силы упругости к коэффициенту жесткости. Коэффициент жесткости определяет упругие свойства материала, используемого для изготовления, может быть использован для выбора материала изготовления в условиях решения конкретной задачи.

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Сила — это физическая векторная величина, которая является мерой действия одного тела на другое.

Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат действия этой силы.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Расчёты на прочность при изгибе

Особую важность при проектировании конструкций и их отдельных элементов играют предварительные расчёты на прочность при возникающих изгибах. По результатам проведенных расчётов устанавливают фактические (реальные) и допустимые напряжения, которые способны выдержать элементы и вся конструкция в целом

Это позволит определить реальный срок службы разработать рекомендации по правильной эксплуатации разработанного объекта

Это позволит определить реальный срок службы разработать рекомендации по правильной эксплуатации разработанного объекта.

Условие прочности выводится в результате сравнения двух показателей. Наибольшего напряжения, которое возникает в поперечном сечении при эксплуатации и допустимого напряжения для конкретного элемента. Прочность зависит от применённого материала, размера детали, способа обработки и его физико-механических и химических свойств.

Для решения поставленной задачи применяются методы и математический аппарат, разработанный в дисциплинах техническая механика, материаловедение и сопротивление материалов. В этом случае применяются:

• дифференциальные зависимости Журавского (семейство дифференциальных уравнений связывающие основные параметры при деформации и их производные);
• способы определения перемещения (наиболее эффективными считаются метод Мора и правило Верещагина);
• семейство принятых гипотез;
• разработанные правила построения графических изображений (построение эпюр).

Расчёт параметров производится в три этапа:

• при проверочном расчёте (вычисляют величину максимального напряжения);
• на этапе проектирования (производится выбор толщины и параметров сечения бруса);
• во время вычисления допустимой нагрузки.

Полученные знаки величин напряжений определяются на основании оценки протекающих физических процессов и направления проекций векторов сил и моментов.

Наиболее наглядными результатами расчёта являются построенные эпюры на поверхности разрабатываемого изделия. Они отражают влияние всех силовых факторов на различные слои деталей. При чистом изгибе эпюры имеют следующие особенности:

• на участке исследуемой балки с отсутствием нагрузки, которая носит распределённый характер, эпюра изображается прямой линией;
• на участке приложения так называемых сосредоточенных сил на эпюре наблюдается изменение направления в форме скачка в том месте к которому приложен вектор силы;
• в точке появления приложенного момента, скачок равен величине этого параметра;
• на участке с распределённой нагрузкой интенсивность воздействия изменяется по линейному закону, а поперечные нагрузки носят степенной характер изменения (чаще всего по параболической кривой, с направлением выпуклости в сторону приложенной нагрузке);
• в границах исследуемого участка функция изгибающего момента приобретает экстремум (на основании методов исследования функций с помощью дифференциального исчисления можно установить характер экстремума – максимум или минимум).

На практике решение систем дифференциальных уравнений может вызвать определённые трудности. Поэтому при расчётах допускаются некоторые прощения, которые не влияют на точность определяемых параметров. К этим упрощениям относятся:

• расчёт производят с учётом нормальных напряжений;
• в качестве основного предположения принимают гипотезу о плоских сечениях;
• продольные волокна не производят дополнительного давления между собой (это позволяет считать, что процессы изгиба носят линейный характер);
• деформация волокон не зависит от их ширины (значения нормальных напряжений постоянные по всей ширине);
• для расчётной балки задают одну плоскость симметрии (все внешние силы лежат в этой плоскости);
• физико-механические характеристики материала подчиняются закону Гука (модуль упругости имеет постоянную величину);
• процессы в балке подчиняются законам плоского изгиба (это допущение вытекает из соотношений геометрических размеров изделия).

Современные методы исследования воздействия внешних сил, внутренних напряжений и моментов позволяют с высокой степенью точности рассчитать прочность каждой детали и всей конструкции в целом. Применение компьютерных методов расчёта, фрактальной геометрии и 3D графики позволяет получить подробную картину происходящих процессов.

Механические свойства

Только при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала. А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры:

1. Жёсткостью называют произведение поперечного сечения профиля на модуль упругости. По этой величине можно судить о пластичности узла конструкции в целом, а не о материале отдельно. Единицей измерения являются килограммы силы.
2. Продольное относительное удлинение — это отношение абсолютного удлинения материала-образца к его общей длине. К примеру, на стержень, длина которого равна 200 миллиметров, приложили некоторую силу. В результате он стал короче на 5 миллиметров. В результате относительное удлинение будет равняться 0,05. Эта величина безразмерная. Для более удобного восприятия иногда её переводят в проценты.
3. Поперечное относительное удлинение рассчитывается точно так же, как и продольное относительное удлинение, но вместо длины берут диаметр стержня. Опытным путём было установлено, что для большего количества материала поперечное меньше продольного удлинения приблизительно в 4 раза.
4. Коэффициент Пуассона. Это отношения относительной продольной к относительной поперечной деформации. При помощи этой величины можно полностью описать под воздействием нагрузки изменения формы.
5. Модуль сдвига описывает упругие свойства под воздействием касательных свойств на образец. Иными словами, когда вектор силы направляется к поверхности тела под 90 градусов. Примером подобных нагрузок служит работа гвоздей на смятие, заклёпок на срез и пр. Этот параметр связан с вязкостью материала.
6. Модуль упругости объёмной характеризует изменение объёма образца для разностороннего равномерного приложения нагрузки. Эта величина является отношением давления объёмного к деформации сжатия объёмной. Как пример можно рассматривать опущенный в воду материал, на который воздействует давление жидкости по всей его площади.

Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства. Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.

У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.

Деформации при растяжении-сжатии

Рассмотрим деформации, возникающие при растяжении (сжатии) стержня. Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l

Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:

При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:

где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии.

Модуль продольной упругости для различных материалов

При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:

Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5.

Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:

Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:

Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).

Расчеты на прочность при кручении

При кручении расчеты на прочность в принципе схожи с теми, что проводятся при растяжении. Только здесь вместо нормальных напряжений появляются касательные напряжения.

На кручение работают, чаще всего, детали, которые называются валами. Их назначение заключается в передаче крутящего момента от одного элемента к другому. При этом вал по всей длине имеет круглое поперечное сечение. Условие прочности для круглого поперечного сечения можно записать  так:

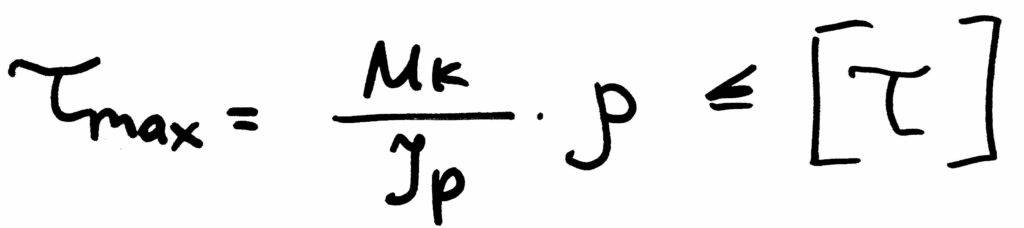
где Ip — полярный момент сопротивления, ρ — радиус круга. Причем по этой формуле можно определить касательное напряжение в любой точке сечения, варьируя значение ρ. Касательные напряжения распределены неравномерно по сечению, их максимальное значение находится в наиболее удаленных точках сечения:

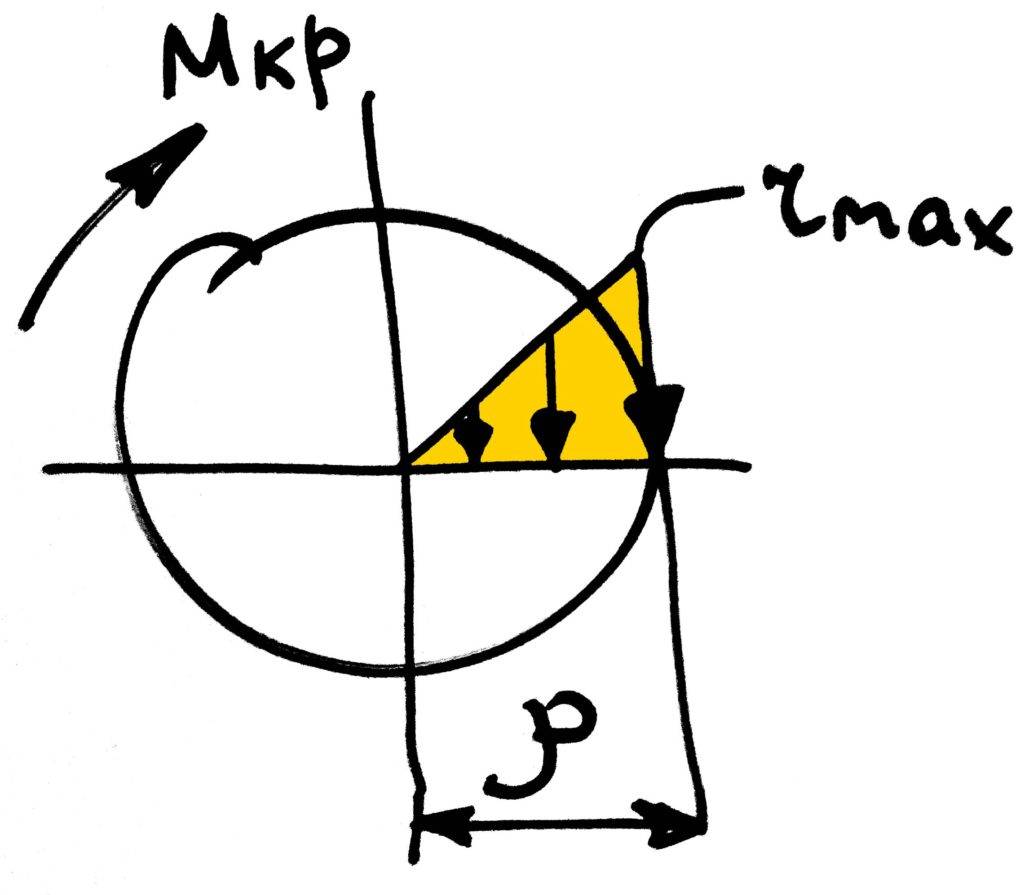
Условие прочности, можно записать несколько проще, используя такую геометрическую характеристику как момент сопротивления:

То бишь максимальные касательные напряжения равны отношению крутящего момента к полярному моменту сопротивления и должны быть меньше либо равны допустимому напряжению. Геометрические характеристики для круга, упомянутые выше можно найти вот так:

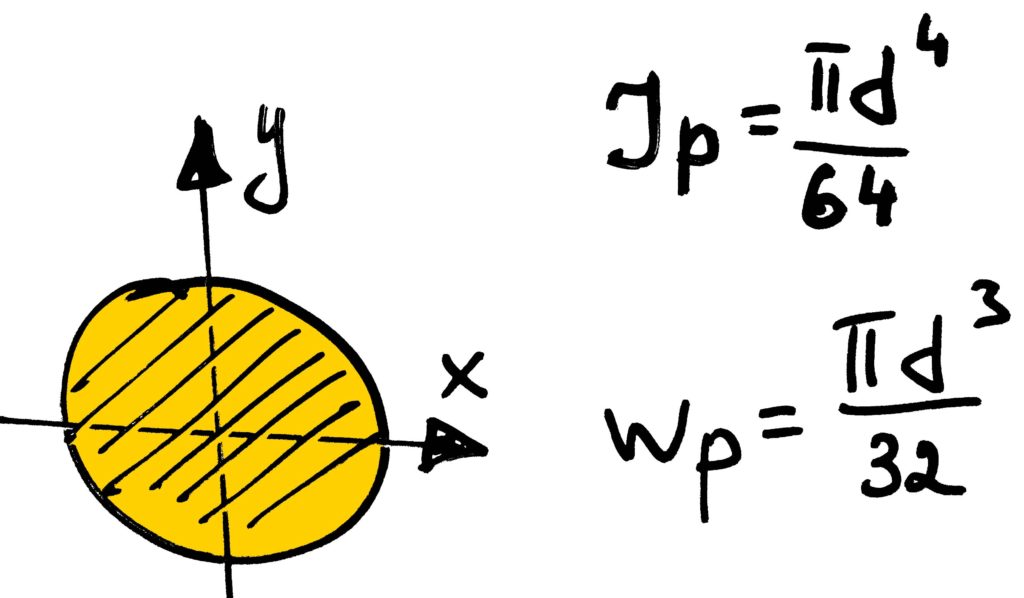
Иногда в задачах встречаются и прямоугольные сечения, для которых момент сопротивления определяется несколько сложнее, но об этом я расскажу в другой статье.

Предел прочности

Предел прочности – максимальное напряжение, которое способно выдержать твердое тело, не разрушаясь.

Если диаграмма напряжения материала имеет вид, соответствующий тому, что показан на графике, то такой материал называется пластичным. У них обычно деформация, при которой происходит разрушение, заметно больше области упругих деформаций. К пластичным материалам относится большинство металлов.

Если материал разрушается при деформации, которая превосходит область упругих деформаций незначительно, то он называется хрупким. Такими материалами считаются чугун, фарфор, стекло и др.

Деформация сдвига имеет аналогичные закономерности и свойства. Ее отличительная особенность состоит в направлении вектора силы: он направлен по касательной относительно поверхности тела. Для поиска величины относительной деформации нам нужно найти значение Δxl, а напряжения – FS (здесь буквой S обозначена та сила, которая действует на единицу площади тела). Для малых деформаций действует следующая формула:

∆xl=1GFS

Буквой G в формуле обозначен коэффициент пропорциональности, также называемый модулем сдвига. Обычно для твердого материала он примерно в 2-3 раза меньше, чем модуль Юнга. Так, для меди E=1,1·1011 Нм2, G=,42·1011 Нм2.

Когда мы имеем дело с жидкими и газообразными веществами, то важно помнить, что у них модуль сдвига равен. При деформации всестороннего сжатия твердого тела, погруженного в жидкость, механическое напряжение будет совпадать с давлением жидкости (p). Чтобы вычислить относительную деформацию, нам нужно найти отношение изменения объема ΔV к первоначальному объему V тела

При малых деформациях

Чтобы вычислить относительную деформацию, нам нужно найти отношение изменения объема ΔV к первоначальному объему V тела. При малых деформациях

При деформации всестороннего сжатия твердого тела, погруженного в жидкость, механическое напряжение будет совпадать с давлением жидкости (p). Чтобы вычислить относительную деформацию, нам нужно найти отношение изменения объема ΔV к первоначальному объему V тела. При малых деформациях

∆VV=1Bp

Буквой B обозначен коэффициент пропорциональности, называемый модулем всестороннего сжатия. Такому сжатию можно подвергнуть не только твердое тело, но и жидкость и газ. Так, у воды B=2,2·109 Нм2, у стали B=1,6·1011Нм2. В Тихом океане на глубине 4 км давление составляет 4·107 Нм2, а относительно изменения объема воды 1,8 %. Для твердого тела, изготовленного из стали, значение этого параметра равно ,025 %, то есть оно меньше в 70 раз. Это подтверждает, что твердые тела благодаря жесткой кристаллической решетке обладают гораздо меньшей сжимаемостью по сравнению с жидкостью, в которой атомы и молекулы связаны между собой не так плотно. Газы могут сжиматься еще лучше, чем тела и жидкости.

От значения модуля всестороннего сжатия зависит скорость, с которой звук распространяется в данном веществе.

Предел упругости и прочности

Если приложенное напряжение превысило допустимое значение, сохраняющее способность тела восстановить первоначальную форму, то после его снятия параметры тела останутся деформированными. Такой исход называется пластической деформацией, а происходит она в результате разрыва межатомных связей. Максимальное напряжение, обеспечивающее допустимую удалённость атомов, что сохраняет связь между ними, а значит и способность тела восстановить исходную форму (упругая деформация), называется пределом упругости. Величина данного показателя делит вещества на упругие и пластичные.

Возврат телу исходной формы производится под влиянием силы упругости, которая подчиняется Закону Гука, выраженному формулой \, где \ – сила упругости, \ — коэффициент жёсткости, x – изменение длины тела. Формула показывает, что сила упругости находится в пропорциональной зависимости с абсолютным изменением длины деформированного тела.

Больший лимит величины, действующей на тело силы, имеет предел прочности, который представлен максимальным значением напряжения, выдерживаемым твёрдым телом, не разрушаясь. В зависимости от показателя этого предела, популярные материалы делятся на прочные и хрупкие. К первым относятся многие металлы, например, титан или хром, а хрупким считается чугун.

Относительная деформация напрямую связана с механическим напряжением тела, которое представлено отношением модуля силы к единице площади воздействия, что отражается в формуле \, где \ – напряжение, \ – сила, \ – площадь. Механическое напряжение представлено давлением и измеряется в Паскалях. Полезность свойств материалов в виде пластичности или упругости, прочности или хрупкости заключена в его деформационных способностях в целом, и широко применяется в строительстве, машиностроении и других инженерных отраслях. Особое значение имеют упругие деформации, которые подлежат тщательному измерению тензометром – прибором, очень точно определяющим деформацию маленькой величины.