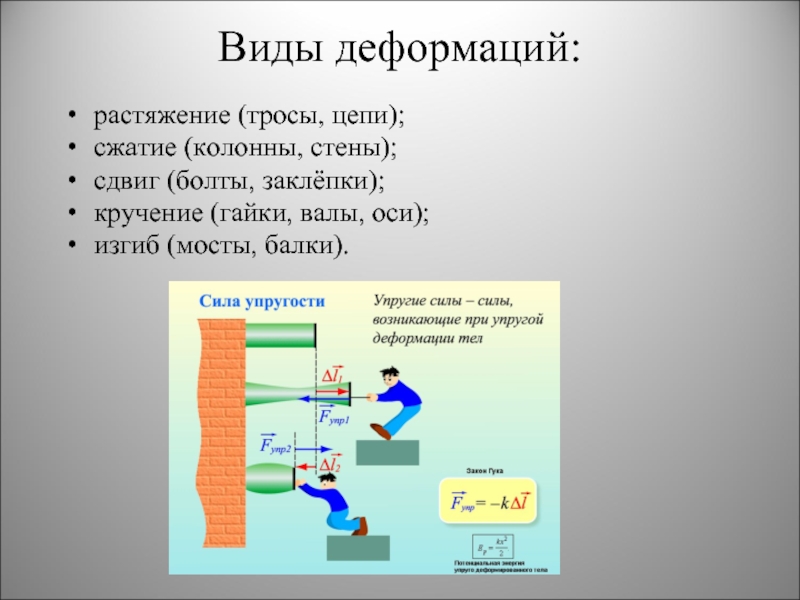
Деформации на примере организма человека
Тело человека подвергается серьезным механическим нагрузкам от собственных усилий и веса, появляющихся по мере физической деятельности. Вообще, деформация (сдвиг) характерна для человеческого организма:
- Сжатие испытывает позвоночник, покровы ступней, нижние конечности.
- Растяжению подвергаются связки, верхние конечности, мышцы, сухожилья.
- Изгиб характерен для конечностей, костей таза, позвонков.
- Кручениям подвергается во время поворота шея, при вращении ее испытывают кисти рук.
Но при превышении показателей предельного напряжения, возможен разрыв, например костей плеча, бедра. В связках же ткани соединяются настолько эластично, что допускается растягивание их в два раза. Кстати, деформация сдвига объясняет всю опасность передвижения женщин на высоких каблуках. Вес тела будет переноситься на пальцы, что приведет к повышению нагрузки на кости в два раза.
По результатам медицинских осмотров, проводимых в школах, из десяти детей лишь одного можно считать здоровым. Как деформации связаны с детским здоровьем? Сдвиг, кручение, сжатие – основные причины нарушения осанки у детей и подростков.
Тестирование сварных швов и расчет деформаций
С целью определения прочности и надежности шва, и выявления возникших дефектов проводится тестирование сварных соединений. Такой контроль позволяет своевременно обнаружить браки и оперативно их устранить.
Для выявления изъянов используют следующие типы контроля:
- разрушающий. Позволяет исследовать физические качества сварного шва, активно применятся на производственных предприятиях;
- неразрушающий. Проводится посредством внешнего осмотра, капиллярного метода, магнитной или ультразвуковой дефектоскопии, контролем на проницаемость и другими способами.
При производстве конструкций с применением сварки одним из важных нюансов является точное определение возможных деформаций и напряжений. Их наличие приводит к отклонениям от первоначальных размеров и форм изделий, понижает прочность конструкций и ухудшает эксплуатационные качества.

Расчет сварочных напряжений и деформаций позволяет проанализировать разные варианты проведения сварочных операций и спланировать их последовательность так, чтобы в процессе работ конструкция подвергалась минимальным напряжениям и образованию дефектов.
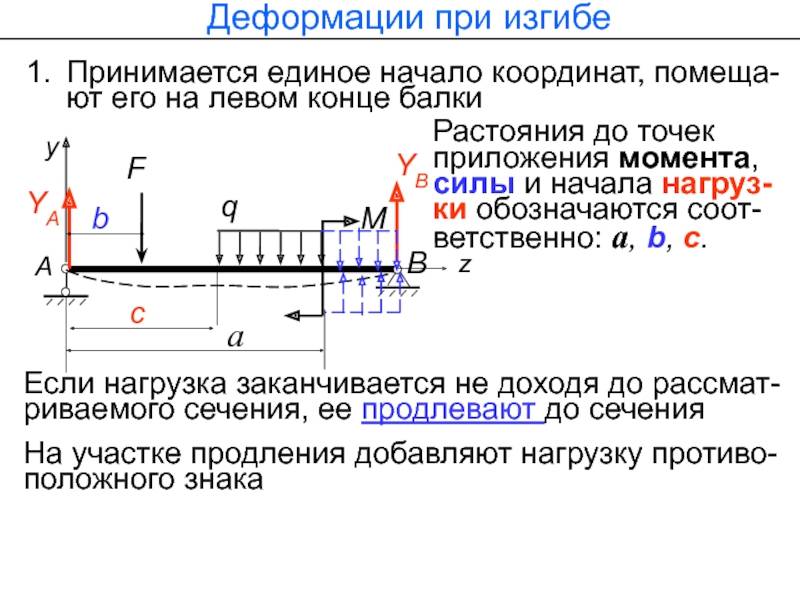
Определение деформаций при изгибе
Касательная к оси кривой стержня в любой точке стержня находится под углом, равным углу поворота сечения в этой точке относительно исходной оси. Тангенс тангенса наклона tg9 = dy / dx. Однако, поскольку фактическое значение угла поворота поперечного сечения при изгибе невелико (порядка 1/1000 радиан), тангенс угла угла равен yuia (tg0 «0), а угол поворота поперечного сечения и зависимости 0 ~ Вы можете найти отношение отклонения в виде dyldx.
Mi> 0 Y Ми <0 О тебе «> у «<О y «> ОМ„ <0 у «<О М> 0 г Рисунок 5.24 Из математического процесса известна следующая зависимость кривизны линии L «в плоскости XOY. K = ± (d2 yIdx2) / (1+ (dy / dx) 2) 3/2. (5,41) Однако, поскольку (dy / dx) 2 = tg20 = b2 «1, формула (5.41) имеет вид K = ± (d2y / dx2). (5,42) Используя зависимость (5.34), соедините кривизну оси стержня с изгибающим моментом Mn и жесткостью сечения E1 {. (5,43) (5,44) K = \ / p = MJ (EIz). Сравнивая уравнения кривизны, полученные в зависимостях (5.42) и (5.43), можно получить дифференциальное уравнение оси изгиба стержня. ± (d2y / dx2) = МДж (EIz),
Его интеграция не сложная. Выбор знака в уравнении (5.44) определяется используемой системой координат. Ранее принятый символ Л / и изгибающего момента (рисунок 5.24, б — е) не зависит от направления осей. Кривизна линии положительна, т. Е. Y «= ^ y / cbc2> 0, когда вогнутая поверхность кривой совпадает с положительным направлением оси ОА (рис. 5.24, б, д), и наоборот (рис. 5.24, в, г) В направлении приема оси ОК знак слева и справа.
Уравнение (5.44) всегда одинаково. Если y «> 0 и Mn> 0, а f ‘
Пример 5.4. Нагрузка приложена к концу силой концентрации F. Жесткость стержня постоянна с длиной, равной EI. Получите начало координат в точке B, которая является жесткой фиксированной точкой стержня. Ось OK направлена вверх, а ось находится справа от OX ~. Для любого сечения на расстоянии x от начала координат изгибающий момент равен L / и = -F (l-x). Дифференциальное уравнение (5.45) оси кривой принимает вид EI (d2y / dx2) -F (l-x).
Интегрирование этого уравнения дает EI (dy / dx) = -F (lx-x2 / 2) + C. При дальнейшей интеграции получается уравнение отклонения. Ely-F (lx2 / 2-x / 6) + Cx + D dO / dx = MK / (EIZ). Чтобы найти уравнения, определяющие деформацию стержней или их угловые и линейные перемещения, необходимо интегрировать уравнение (5.45). После интеграции вы получите уравнение угла поворота Учитывая, что точка взгляда в точке x = 0, прогиб y и угол поворота Q = dy / dx сечения равны нулю, можно видеть, что константы интегрирования C-0 и Z> = 0. Далее свободный конец стержня в точке x = 1 y = -Lg / (ZEG) и угол поворота Q-dy / dx = -Fl2 / (2EI) конца. Знак «-» в представлении угла отклонения и поворота указывает на то, что отклонение выполняется в направлении, противоположном положительному направлению оси OY. Если вы установите его, край будет вращаться по часовой стрелке.
| Определение нормальных напряжений при изгибе | Понятие о теориях прочности |
| Определение касательных напряжений при изгибе | Изгиб с кручением стержней круглого поперечного сечения |
Если вам потребуется помощь по прикладной механике вы всегда можете написать мне в whatsapp.
Испытание на прочность на изгиб
Это испытание создает растягивающее напряжение на выпуклой стороне образца и сжимающее напряжение на противоположной стороне. Отношение пролета к глубине контролируется для минимизации напряжения сдвига. Для большинства материалов считается отношение L / d равным 16.
По сравнению с испытанием на изгиб при трехточечном изгибе, при испытании на изгиб при четырехточечном изгибе не наблюдаются сдвиговые силы в зоне между двумя нагружающими штифтами. Таким образом, испытание на четырехточечный изгиб наиболее подходит для хрупких материалов, которые не могут выдерживать напряжения сдвига.
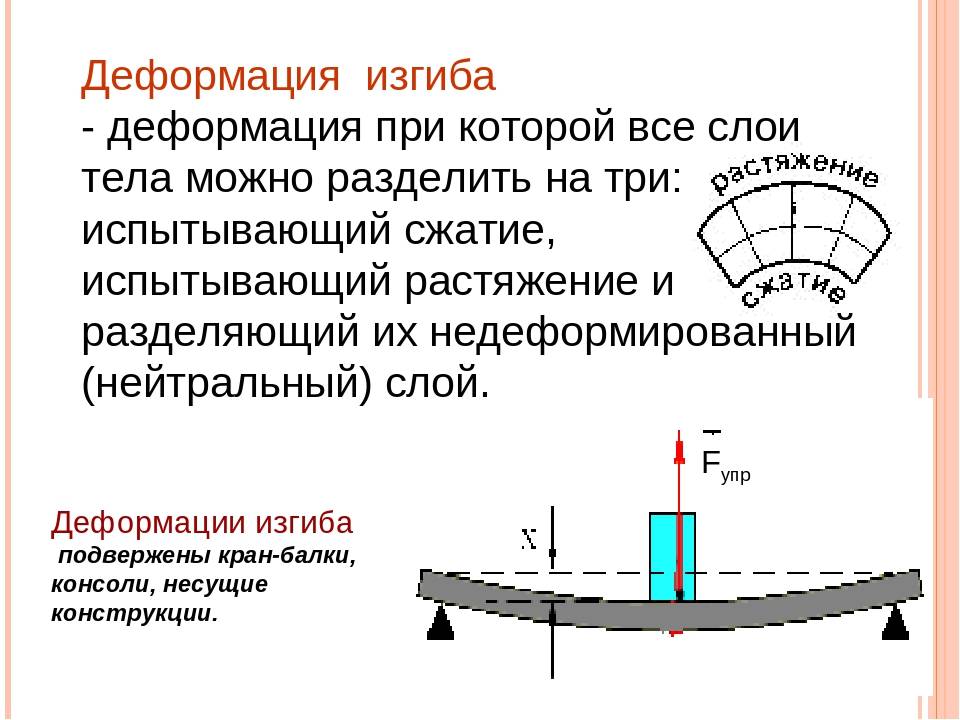
Чистый и поперечный изгиб балки
Если единственным внешним воздействием является сила, вызывающая изгибающий момент, такой изгиб называется чистым. Собственным весом изделия можно пренебречь.
При изгибе балки вводят следующие допущения:
- Во всех сечениях присутствуют только нормальные напряжения.
- Их разбивают на два слоя. Один называются растянутым, другой сжатым. Границей этих зон является линия сечения. Величина нормальных напряжений нейтрального слоя равны нулю.
- Продольный элемент детали подвержен осевому напряжению. Оно вызывает растяжение или сжатие. Соседние слои не вступают во взаимодействие друг с другом.
- При сохранении геометрической формы верхнего слоя все внутренние слои сохраняют прежнюю форму. Воздействие внешней силы остаётся перпендикулярным к поверхности детали.
Если на поверхность детали производится воздействие под углом к поверхности — такой изгиб называется поперечным. При поперечном изгибе в слоях детали (например, балки) возникают два вида напряжений. Одни называются нормальными, другие касательными. В этом случае все сечения не будут плоскими, но искривлёнными. На определённых уровнях искривления при изгибе не достаточно большие. Это позволяет при расчёте применять все формулы, справедливые для чистого изгиба.
Чистый и поперечный изгиб балки
Если единственным внешним воздействием является сила, вызывающая изгибающий момент, такой изгиб называется чистым. Собственным весом изделия можно пренебречь.
При изгибе балки вводят следующие допущения:
- Во всех сечениях присутствуют только нормальные напряжения.
- Их разбивают на два слоя. Один называются растянутым, другой сжатым. Границей этих зон является линия сечения. Величина нормальных напряжений нейтрального слоя равны нулю.
- Продольный элемент детали подвержен осевому напряжению. Оно вызывает растяжение или сжатие. Соседние слои не вступают во взаимодействие друг с другом.
- При сохранении геометрической формы верхнего слоя все внутренние слои сохраняют прежнюю форму. Воздействие внешней силы остаётся перпендикулярным к поверхности детали.


Если на поверхность детали производится воздействие под углом к поверхности — такой изгиб называется поперечным. При поперечном изгибе в слоях детали (например, балки) возникают два вида напряжений. Одни называются нормальными, другие касательными. В этом случае все сечения не будут плоскими, но искривлёнными. На определённых уровнях искривления при изгибе не достаточно большие. Это позволяет при расчёте применять все формулы, справедливые для чистого изгиба.
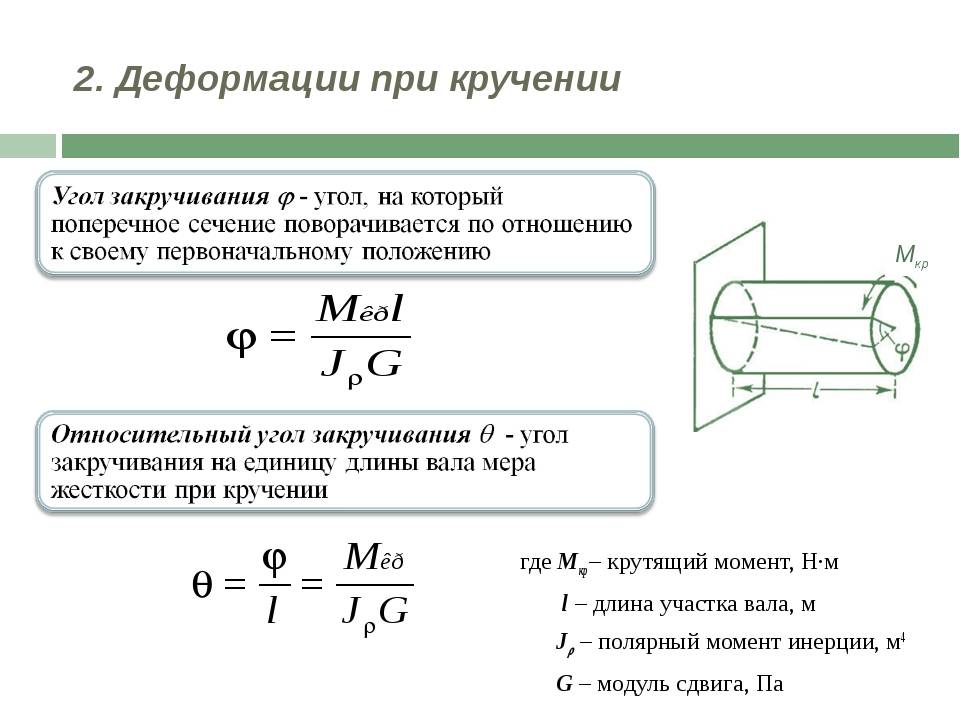
Дифференциальные зависимости Журавского.
Между интенсивностью q распределенной нагрузки, выражениями для поперечной силы Q и изгибающего момента М установлены дифференциальные зависимости:
На основе этих зависимостей можно выделить следующие общие закономерности эпюр поперечных сил Q и изгибающих моментов М:
Особенности эпюр внутренних силовых факторов при изгибе.
1.
На участке балки, где нет распределенной нагрузки, эпюра Q представленапрямой линией , параллельной базе эпюре, а эпюра М — наклонной прямой (рис. а).
2.
В сечении, где приложена сосредоточенная сила, на эпюре Q должен бытьскачок , равный значению этой силы, а на эпюре М —точка перелома (рис. а).
3.
В сечении, где приложен сосредоточенный момент, значение Q не изменяется, а эпюра М имеетскачок , равный значению этого момента, (рис. 26, б).
4.
На участке балки с распределенной нагрузкой интенсивности q эпюра Q изменяется по линейному закону, а эпюра М — по параболическому, причемвыпуклость параболы направлена навстречу направлению распределенной нагрузки (рис. в, г).
5.
Если в пределах характерного участка эпюра Q пересекает базу эпюры, то в сечении, где Q = 0, изгибающий момент имеет экстремальное значение Mmax или Mmin (рис. г).
Прогноз
Патология поддается лечению, удается восстановить функции желчного пузыря и избежать развития заболеваний органов пищеварительного тракта.
При своевременном выявлении нарушения, адекватном лечении и диете полное выздоровление примерно у 95% пациентов с перегибами желчного пузыря наступает через 3-6 месяцев.
Прогноз может быть неблагоприятным в случае полного перекрытия оттока желчи. Может произойти разрыв стенок с вытеканием желчи в брюшную полость. В таких случаях происходит удаление органа. Эта ситуация опасна инфицированием. Открытые перфорации возникают редко, но в 30% заканчиваются летальным исходом.
Внутренние силовые факторы при изгибе балки.
При плоском поперечном изгибе в сечениях балки возникают два внутренних силовых фактора: поперечная сила Q и изгибающий момент М. Для их определения используют метод сечений. Поперечная сила Q в сечении балки равна алгебраической сумме проекций на плоскость сечения всех внешних сил, действующих по одну сторону от рассматриваемого сечения.
Правило знаков для поперечных сил Q:
Изгибающий момент М в сечении балки равен алгебраической сумме моментов относительно центра тяжести этого сечения всех внешних сил, действующих по одну сторону от рассматриваемого сечения.
Правило знаков для изгибающих моментов M:
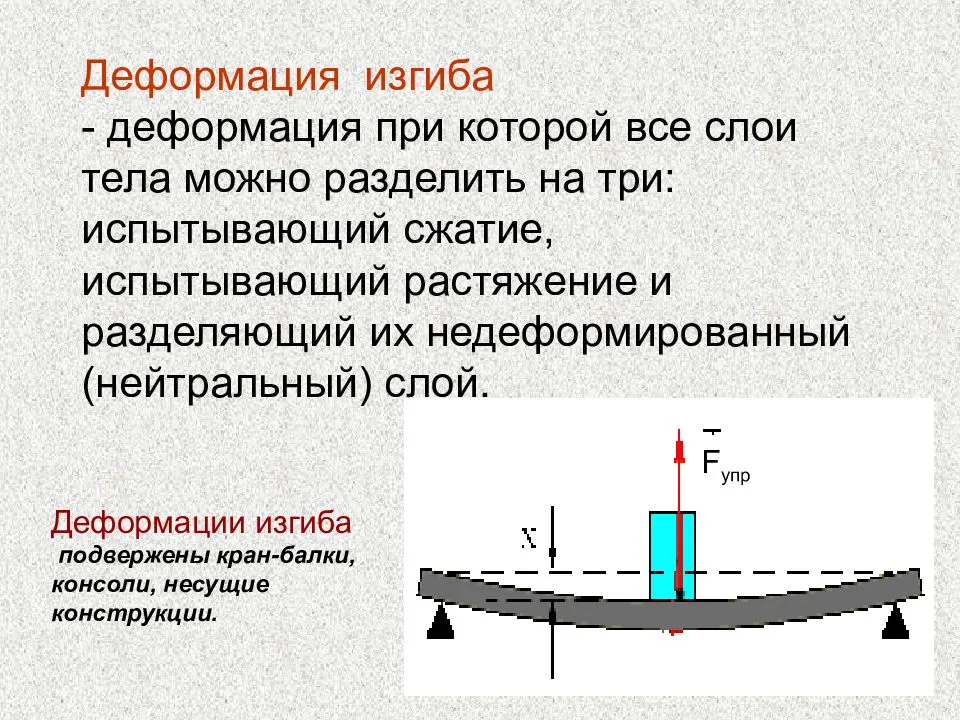
Чистый и поперечный изгиб балки
Если единственным внешним воздействием является сила, вызывающая изгибающий момент, такой изгиб называется чистым. Собственным весом изделия можно пренебречь.
При изгибе балки вводят следующие допущения:
- Во всех сечениях присутствуют только нормальные напряжения.
- Их разбивают на два слоя. Один называются растянутым, другой сжатым. Границей этих зон является линия сечения. Величина нормальных напряжений нейтрального слоя равны нулю.
- Продольный элемент детали подвержен осевому напряжению. Оно вызывает растяжение или сжатие. Соседние слои не вступают во взаимодействие друг с другом.
- При сохранении геометрической формы верхнего слоя все внутренние слои сохраняют прежнюю форму. Воздействие внешней силы остаётся перпендикулярным к поверхности детали.
Если на поверхность детали производится воздействие под углом к поверхности — такой изгиб называется поперечным. При поперечном изгибе в слоях детали (например, балки) возникают два вида напряжений. Одни называются нормальными, другие касательными. В этом случае все сечения не будут плоскими, но искривлёнными. На определённых уровнях искривления при изгибе не достаточно большие. Это позволяет при расчёте применять все формулы, справедливые для чистого изгиба.
Прочность и деформации
Несмотря на многообразие живого и неживого мира, на создание человеком многочисленных материальных объектов, у всех предметов и живых существ есть общее свойство – прочность. Под ней принято понимать способность материала сохраняться на протяжении длительного временного промежутка без видимых разрушений. Существует прочность конструкций, молекул, сооружений. Эта характеристика уместна для кровеносных сосудов, человеческих костей, кирпичной колонны, стекла, воды. Деформация сдвига – вариант проверки сооружения на прочность.
Применение разных видов деформаций человеком имеет глубокие исторические корни. Все начиналось с желания соединить между собой палку и острый наконечник, чтобы охотиться на древних животных. Уже в те далекие времена человека интересовала деформация. Сдвиг, сжатие, растяжение, изгиб помогали ему создавать жилища, орудия труда, готовить пищу. По мере развития техники человечеству удалось использовать различные виды деформаций так, чтобы они приносили весомую пользу.

Расчёты на прочность при изгибе
Особую важность при проектировании конструкций и их отдельных элементов играют предварительные расчёты на прочность при возникающих изгибах. По результатам проведенных расчётов устанавливают фактические (реальные) и допустимые напряжения, которые способны выдержать элементы и вся конструкция в целом
Это позволит определить реальный срок службы разработать рекомендации по правильной эксплуатации разработанного объекта
Это позволит определить реальный срок службы разработать рекомендации по правильной эксплуатации разработанного объекта.
Условие прочности выводится в результате сравнения двух показателей. Наибольшего напряжения, которое возникает в поперечном сечении при эксплуатации и допустимого напряжения для конкретного элемента. Прочность зависит от применённого материала, размера детали, способа обработки и его физико-механических и химических свойств.
Для решения поставленной задачи применяются методы и математический аппарат, разработанный в дисциплинах техническая механика, материаловедение и сопротивление материалов. В этом случае применяются:
- дифференциальные зависимости Журавского (семейство дифференциальных уравнений связывающие основные параметры при деформации и их производные);
- способы определения перемещения (наиболее эффективными считаются метод Мора и правило Верещагина);
- семейство принятых гипотез;
- разработанные правила построения графических изображений (построение эпюр).
Расчёт параметров производится в три этапа:
- при проверочном расчёте (вычисляют величину максимального напряжения);
- на этапе проектирования (производится выбор толщины и параметров сечения бруса);
- во время вычисления допустимой нагрузки.
Полученные знаки величин напряжений определяются на основании оценки протекающих физических процессов и направления проекций векторов сил и моментов.
Наиболее наглядными результатами расчёта являются построенные эпюры на поверхности разрабатываемого изделия. Они отражают влияние всех силовых факторов на различные слои деталей. При чистом изгибе эпюры имеют следующие особенности:
- на участке исследуемой балки с отсутствием нагрузки, которая носит распределённый характер, эпюра изображается прямой линией;
- на участке приложения так называемых сосредоточенных сил на эпюре наблюдается изменение направления в форме скачка в том месте к которому приложен вектор силы;
- в точке появления приложенного момента, скачок равен величине этого параметра;
- на участке с распределённой нагрузкой интенсивность воздействия изменяется по линейному закону, а поперечные нагрузки носят степенной характер изменения (чаще всего по параболической кривой, с направлением выпуклости в сторону приложенной нагрузке);
- в границах исследуемого участка функция изгибающего момента приобретает экстремум (на основании методов исследования функций с помощью дифференциального исчисления можно установить характер экстремума – максимум или минимум).
На практике решение систем дифференциальных уравнений может вызвать определённые трудности. Поэтому при расчётах допускаются некоторые прощения, которые не влияют на точность определяемых параметров. К этим упрощениям относятся:
- расчёт производят с учётом нормальных напряжений;
- в качестве основного предположения принимают гипотезу о плоских сечениях;
- продольные волокна не производят дополнительного давления между собой (это позволяет считать, что процессы изгиба носят линейный характер);
- деформация волокон не зависит от их ширины (значения нормальных напряжений постоянные по всей ширине);
- для расчётной балки задают одну плоскость симметрии (все внешние силы лежат в этой плоскости);
- физико-механические характеристики материала подчиняются закону Гука (модуль упругости имеет постоянную величину);
- процессы в балке подчиняются законам плоского изгиба (это допущение вытекает из соотношений геометрических размеров изделия).
Современные методы исследования воздействия внешних сил, внутренних напряжений и моментов позволяют с высокой степенью точности рассчитать прочность каждой детали и всей конструкции в целом. Применение компьютерных методов расчёта, фрактальной геометрии и 3D графики позволяет получить подробную картину происходящих процессов.
Деформации при растяжении сжатии
При растяжении/сжатии бруса могут возникать 2 вида деформации. Первый – упругая, второй – пластическая. Для упругой деформации характерно восстановление первоначальных параметров после прекращения воздействия. В случае пластической стадии деформации материала он утрачивает и не восстанавливает форму и размеры. Величина воздействия для перехода одного вида в другой называется пределом текучести.
Для расчета перемещения при растяжении бруса или стержня следует использовать метод разделения на участки, в рамках которых осуществляется приложение внешних воздействий. В точках воздействия силы следует вычислить величину изменения длины, используя формулу: Δl=Nl/EA. Как видно она зависит от жесткости сечения, длины бруса или стержня и величины действующей продольной силы. Итоговым перемещением для бруса целиком будет сумма всех частичных перемещений, рассчитанных для точек приложения силы.

Поперечные деформации бруса (становится более толстым при сжатии и тонким при растяжении) также характеризуются абсолютной и относительной величиной деформации. Первая – разность между размером сечения после и до приложения внешних воздействий, вторая – отношение абсолютной деформации к его исходному размеру. Коэффициент Пуассона, отражающий линейную зависимость продольной и поперечной деформаций, определяет упругие качества материалов и считается неизменным для растяжения и сжатия. Продольные наиболее наглядно отражают процессы, происходящие в брусе или стержне при внешнем воздействии. Зная величину любой из них (продольной или поперечной) и используя коэффициент Пуассона, можно рассчитать значение неизвестной.
Для определения величины деформации пружины при растяжении можно применить закон Гука для пружин:
F=kx
В данном случае х – увеличение длины пружины, k – коэффициент жесткости (единица измерения Н/м), F – сила упругости, направленная в противоположную от смещения сторону. Величина абсолютной деформации будет равна отношению силы упругости к коэффициенту жесткости. Коэффициент жесткости определяет упругие свойства материала, используемого для изготовления, может быть использован для выбора материала изготовления в условиях решения конкретной задачи.
Методы расчета перемещений
Существует несколько способов расчета линейных y и угловых θ перемещений при изгибе:
Метод начальных параметров (МНП)
Перемещения рассчитываются по уравнениям МНП
 Считается относительно простым методом расчета перемещений в прямых балках с постоянной жесткостью сечения. Данный способ не применим для расчета прогибов и углов наклона в балках переменного сечения, с изогнутой или ломаной осью и в рамах.Подробнее >>
Считается относительно простым методом расчета перемещений в прямых балках с постоянной жесткостью сечения. Данный способ не применим для расчета прогибов и углов наклона в балках переменного сечения, с изогнутой или ломаной осью и в рамах.Подробнее >>
Интеграл Мора
Интеграл Мора относится к энергетическим методам расчета перемещений. В отличие от МНП позволяет определять линейные и угловые перемещения для любых систем. Подробнее >>
Способ Верещагина
Данный способ расчета перемещений представляет собой графическую интерпретацию интеграла Мора, особенностью которой является «перемножение эпюр» грузовой и единичных схем. Подробнее >>
Метод интегрирования дифференциального уравнения упругой линии балки
Непосредственное интегрирование дифференциального уравнения упругой линии является одним из наиболее универсальных способов расчета перемещений в балках. Может применяться без ограничений к балкам любой формы.
По результатам расчета перемещений сечений балки строится линия изогнутой оси балки (либо эпюра прогибов), с указанием числовых значений прогибов и углов наклона в характерных сечениях.
 Эти вычисления и построения необходимы для проверки балок на жесткость.
Эти вычисления и построения необходимы для проверки балок на жесткость.
Примеры решения задач >Лекции по сопромату >
Дифференциальные зависимости Журавского.
Между интенсивностью q распределенной нагрузки, выражениями для поперечной силы Q и изгибающего момента М установлены дифференциальные зависимости:
На основе этих зависимостей можно выделить следующие общие закономерности эпюр поперечных сил Q и изгибающих моментов М:
Особенности эпюр внутренних силовых факторов при изгибе.
1.
На участке балки, где нет распределенной нагрузки, эпюра Q представленапрямой линией , параллельной базе эпюре, а эпюра М — наклонной прямой (рис. а).
2.
В сечении, где приложена сосредоточенная сила, на эпюре Q должен бытьскачок , равный значению этой силы, а на эпюре М —точка перелома (рис. а).
3.
В сечении, где приложен сосредоточенный момент, значение Q не изменяется, а эпюра М имеетскачок , равный значению этого момента, (рис. 26, б).
4.
На участке балки с распределенной нагрузкой интенсивности q эпюра Q изменяется по линейному закону, а эпюра М — по параболическому, причемвыпуклость параболы направлена навстречу направлению распределенной нагрузки (рис. в, г).
5.
Если в пределах характерного участка эпюра Q пересекает базу эпюры, то в сечении, где Q = 0, изгибающий момент имеет экстремальное значение Mmax или Mmin (рис. г).
Методы расчета перемещений
Существует несколько способов расчета линейных y и угловых θ перемещений при изгибе:
Метод начальных параметров (МНП)
Перемещения рассчитываются по уравнениям МНП
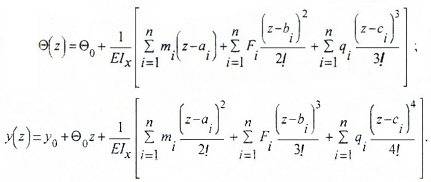
Считается относительно простым методом расчета перемещений в прямых балках с постоянной жесткостью сечения. Данный способ не применим для расчета прогибов и углов наклона в балках переменного сечения, с изогнутой или ломаной осью и в рамах.Подробнее >>
Интеграл Мора
Интеграл Мора относится к энергетическим методам расчета перемещений. В отличие от МНП позволяет определять линейные и угловые перемещения для любых систем. Подробнее >>
Способ Верещагина
Данный способ расчета перемещений представляет собой графическую интерпретацию интеграла Мора, особенностью которой является «перемножение эпюр» грузовой и единичных схем. Подробнее >>
Метод интегрирования дифференциального уравнения упругой линии балки
Непосредственное интегрирование дифференциального уравнения упругой линии является одним из наиболее универсальных способов расчета перемещений в балках. Может применяться без ограничений к балкам любой формы.
По результатам расчета перемещений сечений балки строится линия изогнутой оси балки (либо эпюра прогибов), с указанием числовых значений прогибов и углов наклона в характерных сечениях.
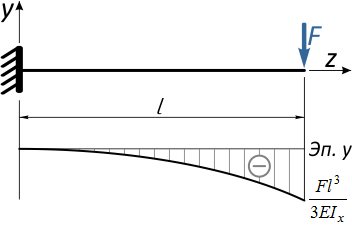
Эти вычисления и построения необходимы для проверки балок на жесткость.
Примеры решения задач >Лекции по сопромату >
Деформация твёрдого тела: её виды, измерение
Под воздействием внешних сил твёрдые тела меняют свою форму и объем, т.е. деформируются.
В результате действия приложенных к телу сил частицы, из которых оно состоит, перемещаются. Изменяются расстояния между атомами, их взаимное расположение. Это явление называют деформацией.
Если после прекращения действия силы тело возвращает свою первоначальную форму и объём, то такая деформация называется упругой, или обратимой. В этом случае атомы снова занимают положение, в котором они находились до того, как на тело начала действовать сила.
Если мы сожмём резиновый мячик, он изменит форму. Но тут же восстановит её, как только мы его отпустим. Это пример упругой деформации.
Если же в результате действия силы атомы смещаются от положений равновесия на такие расстояния, что межатомные связи на них уже не действуют, они не могут вернуться в первоначальное состояние и занимают новые положения равновесия. В этом случае в физическом теле происходят необратимые изменения.
Сдавим кусочек пластилина. Свою первоначальную форму он не сможет вернуть, когда мы прекратим воздействовать на него. Он деформировался необратимо. Такую деформацию называют пластичной, или необратимой.
Необратимые деформации могут также происходить постепенно с течением времени, если на тело воздействует постоянная нагрузка, или под влиянием различных факторов в нём возникает механическое напряжение. Такие деформации называются деформациями ползучести.
Например, когда детали и узлы каких-то агрегатов во время работы испытывают серьёзные механические нагрузки, а также подвергаются значительному нагреву, в них со временем наблюдается деформация ползучести.
Под воздействием одной и той же силы тело может испытывать упругую деформацию, если сила приложена к нему на короткое время. Но если эта же сила будет воздействовать на это же тело длительно, то деформация может стать необратимой.
Величина механического напряжения, при которой деформация тела всё ещё будет упругой, а само тело восстановит свою форму после снятия нагрузки, называется пределом упругости. При значениях выше этого предела тело начнёт разрушаться. Но разрушить твёрдое тело не так-то просто. Оно сопротивляется. И это его свойство называется прочностью.
Когда два автомобиля, соединённые буксировочным тросом, начинают движение, трос подвергается деформации. Он натягивается, а его длина увеличивается. А когда они останавливаются, натяжение ослабевает, и длина троса восстанавливается. Но если трос недостаточно прочный, он просто разорвётся.