Модуль зубьев зубчатого колеса

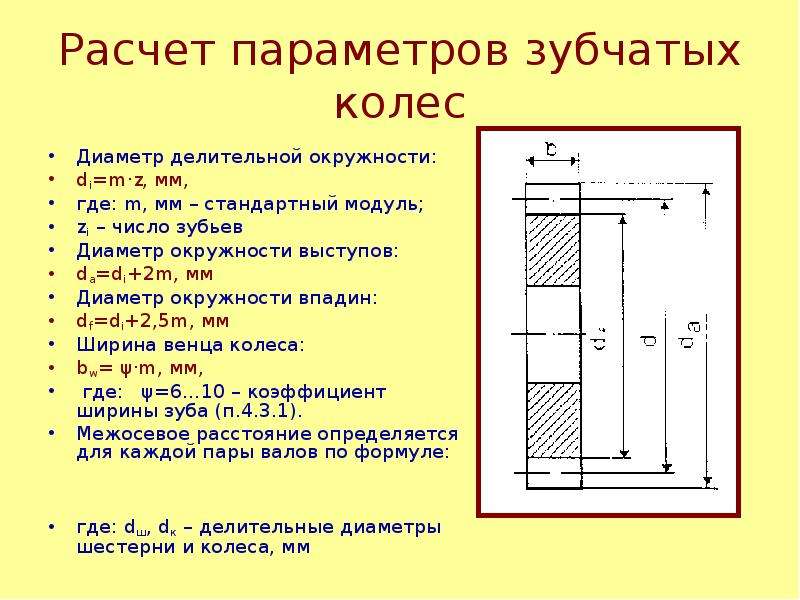
Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D_e получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

Диаметр окружности впадин D_i соответствует D_e за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

что соответствует формуле:

и если выполнить подстановку, то получим:

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s_в, получаем формулы для ширины впадины

• для отлитых зубцов: s_в=πm-1,53m=1,61m:
• для выполненных путем фрезерования- s_в= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D_e получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

Диаметр окружности впадин D_i соответствует D_e за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

что соответствует формуле:

и если выполнить подстановку, то получим:

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s_в, получаем формулы для ширины впадины

• для отлитых зубцов: s_в=πm-1,53m=1,61m:
• для выполненных путем фрезерования- s_в= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Что такое модуль зубчатого колеса

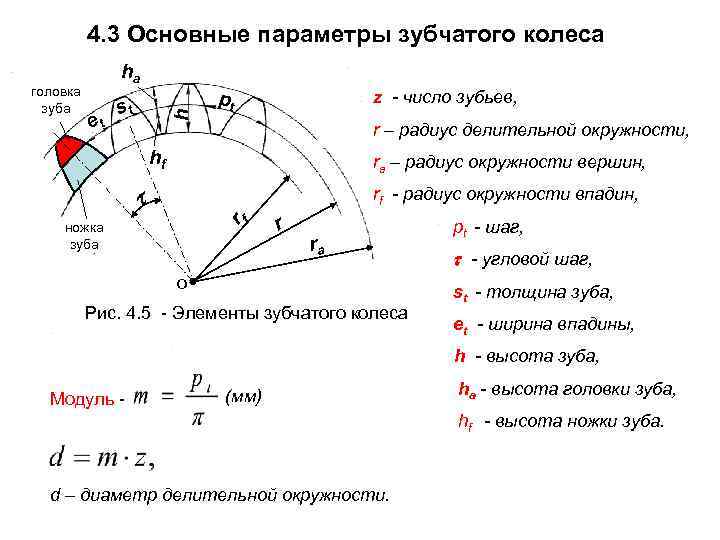
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров

• диаметр;
• число зубьев;
• шаг;
• высота зубца;
• и некоторые другие.

Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.

В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.

Для расчета этого параметра применяют следующие формулы:

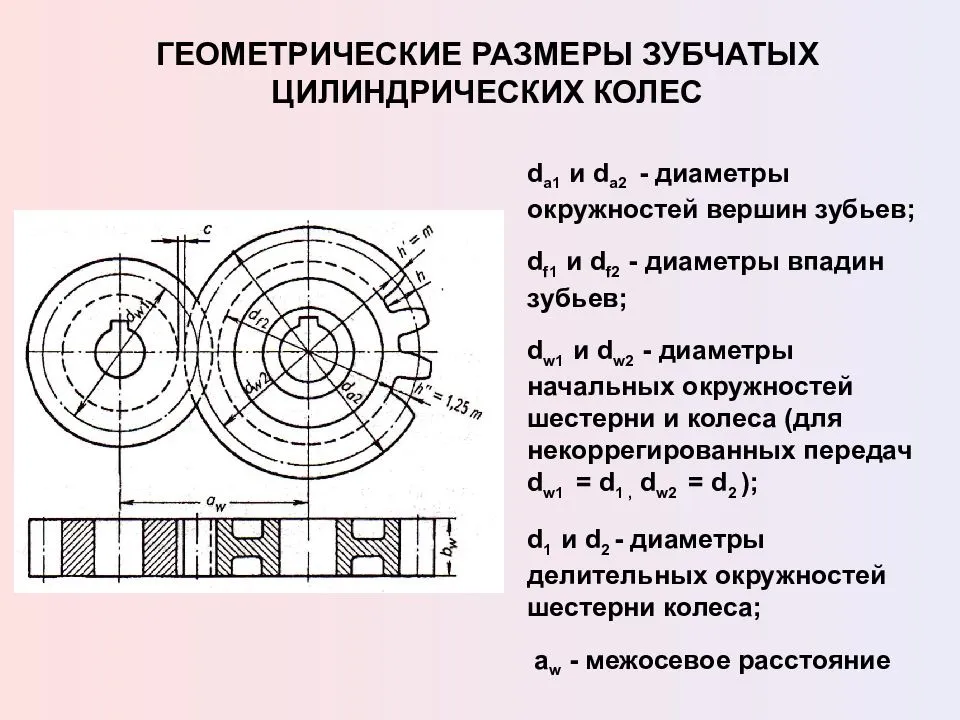
Параметры зубчатых колес

Модуль зубчатого колеса можно рассчитать и следующим образом:

где h — высота зубца.

где De — диаметр окружности выступов,а z — число зубьев.

Что же такое модуль шестерни?

это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.

Конструкция

Червячная передача получила свое название по ведущей детали, передающей крутящий момент. Ведомая деталь имеет зуб с косой нарезкой. По ободу радиальное занижение поверхности. Это увеличивает линию контакта нити резьбы и зуба.

Оси вращение деталей располагаются под углом. Обычно это 90°, но может быть 45°. Применяется такое расположение деталей в сильно нагруженных тихоходных передачах, со скоростью движения точки на наружной поверхности менее 5 м/сек.

При взаимодействии передачи поверхность резьбы не толкает зубья в направлении вращения, а скользит по эвольвенте, как бы отодвигая ее. В результате возникает сильное трение и нагрев деталей в месте контакта.

Червячная пара должна хорошо смазываться, охлаждаться и обладать антифрикционными свойствами. Материал червяка изменять нельзя, он нарезается из хромистой стали и проходит закалку, шлифовку поверхности резьбы или шугаровку – обработку пластиной с малой глубиной реза. Инструмент скорее продавливает поверхность резьбы, чем режет ее. Создается на верхнем слое наклеп, упрочняющий рабочую поверхность, делающий ее гладкой.

Материал для венца

Венец зубчатого колеса выполняется из относительно мягкого материала с высоким сопротивлением стиранию. В основном применяются оловянные бронзы и латунь. Для низкоскоростных передач с ручным управлением можно делать венец из серого чугуна. В зависимости от скорости вращения зубчатый венец изготавливается из материала:

• 5 – 25 м/сек – оловянистые бронзы ОФ10-1, ОНФ;
• ≤ 5 м/сек – Бр.АЖ9-4, алюминиево-железистая бронза;
• ≤ 2 м/сек – венец может быть из чугуна.

Бронза стоит значительно дороже стали и мягче. Полностью из нее делаются детали, размеры которых в пределах 160 мм. Большие детали вытачиваются из стали и бронзовый на них только венец. Он на горячо сажается на вал и закрепляется штифтами по линии соединения, чтобы венец не прокручивался. После остывания производится чистовая обработка колеса и нарезается зуб.

Расчет диаметра

Диаметр колеса рассчитывается по средней линии зуба – ширины зуба и впадины равны. Наружный, используемый для изготовления и расчетов радиус, определяется теоретически. После завершения обработки, он находится за пределами фактического обода колеса.

Скольжение происходит по линии делительного диаметра – середина зуба по высоте. Он рассчитывается по формуле:

где d₂ — делительный диаметр шестерни; m – модуль; z₂ – количество зубьев колеса.

Наружный радиус зуба имеет один центр с осью червяка.

Ширина зубчатого венца

Ширину венца червячного колеса определяют по числу витков винта по формуле:

где b₂ – ширина венца; 0,315 и 0,355 – расчетный коэффициент; Z₁ – количество заходов винтовой резьбы; a – межцентровое расстояние; a_w – расстояние с учетом смещения червяка относительно зубчатого колеса.

Расстояние смещения определяет размер зазора между рабочими элементами деталей.

В чем заключаются отличия между шестеренкой и зубчатым колесом

Между шестеренкой и зубчатым колесом при детальном рассмотрении имеются определенные различия:

1. Зубчатые колеса используются в механизмах посложнее, тогда как шестеренки – это, как говорится, мастера на все руки.
2. Используются шестеренки преимущественно парами, тогда как зубчатое колесо можно использовать в том или ином механизме в единственном экземпляре.
3. Размеры ведомых шестерен и зубчатых колес могут сильно отличаться друг от друга. Зачастую зубчатое колесо имеет больший диаметр, чем шестеренка, особенно, если используется в мощных системах.

Исходя из всех вышеприведенных фактов, можно сказать, что по своему функционалу шестеренка и зубчатое колесо является примерно одним и тем же элементом. Различия между ними могут быть заметны только в каких-то сложных механизмах, так как они по-разному воздействуют на результат, однако большинство людей, имевших с этим дело, нередко утверждают, что формальной разницы между данными элементами нет.

Электроника и техникаКомментировать

Что такое модуль зубчатого колеса

Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров

• диаметр;
• число зубьев;
• шаг;
• высота зубца;
• и некоторые другие.

Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.

В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.

Для расчета этого параметра применяют следующие формулы:

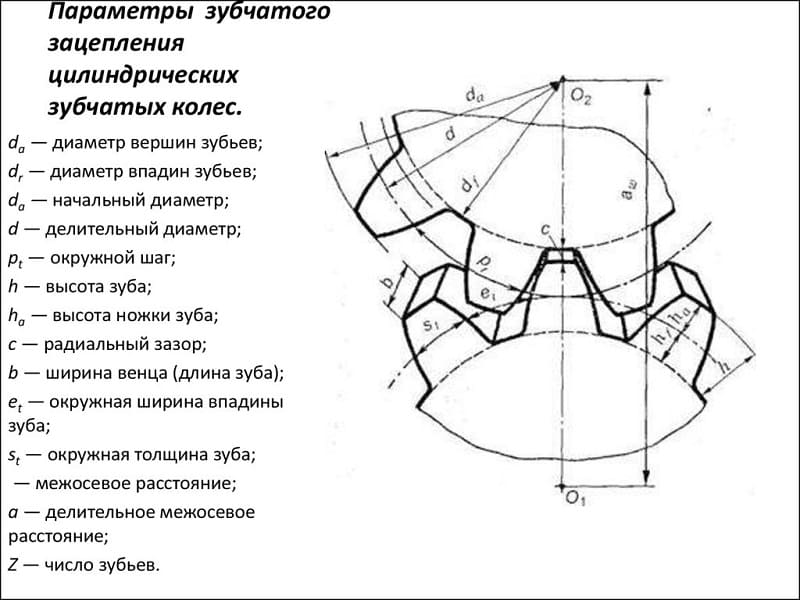
Параметры зубчатых колес

Модуль зубчатого колеса можно рассчитать и следующим образом:

где h — высота зубца.

где De — диаметр окружности выступов,а z — число зубьев.

Что же такое модуль шестерни?

это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.

Подытожим

Расчетные чертежи и схемы для шестеренок различных конфигураций преимущественно совпадают для косых и прямозубчатых версий. Основные различия возникают при расчетах на прочность. В графических отображениях применяются характеристики, ориентированные на типовые габаритные размеры шестеренок. Среди представленного ассортимента на рынке вполне реально подобрать зубчатое колесо с необходимыми характеристиками и прочностными показателями.

Не редко на конвейерных линиях из строя выходят узлы и агрегаты. Ремонт конвейерных лент от специалистов быстро вернет ваше оборудование в строй.

Прямозубые и косозубые колесики

Модуль и диаметр шестерни прямозубого типа — один из самых востребованных видов. Зубцы размещаются в радиальных плоскостях, а площадь контакта пары колес параллельна оси вращения. Аналогичным образом располагаются оси обеих шестерен.

Косозубые колесики представляют собой усовершенствованную вариацию вышеуказанной модификации. Зубцы находятся под определенным углом к вращательной оси. Зацепление осуществляется плавней и тише, что позволяет эксплуатировать элементы в малошумных приспособлениях, гарантируя передачу большего крутящего момента на высокой скорости. К минусам относят увеличенную площадь контакта зубцов, провоцирующую повышенное трение и нагрев деталей. Это чревато ослаблением мощности и повышенным расходом смазки. Кроме того, механическое воздействие вдоль оси шестерни требует использования упорных подшипников для монтажа вала.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

Читать также: Измерение твердости металла по бринеллю

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

что соответствует формуле:

и если выполнить подстановку, то получим:

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины

• для отлитых зубцов: sв=πm-1,53m=1,61m:
• для выполненных путем фрезерования- sв= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Стандарты зубчатых передач США

Вместо модуля для стандартизации зубча­тых передач в США используется показатель количества зубьев на 1 дюйм (25,4 мм) диа­метра делительной окружности или диамет­ральный модуль (питч) (Р):

Р = z/d = z/(z • m/25,4) =25,4/m

Для перевода стандарта США в европейский стандарт служит зависимость:

m = 25,4 мм / P

Размещение зубьев в пределах диаметраль­ного модуля называется окружным шагом зацепления (CP):

CP = (25,4 мм / P) π.

Табл. Стандарты зубчатых передач

Полная высота зуба

В стандартах США полная высота зуба обо­значается как высота головки h_a = т, что соответствует величине т в стандартах Гер­мании.

Ножка зуба

Обозначается так же, как и полная вы­сота зуба, но расчет головки зуба основы­вается на использовании своего модуля. Пример обозначения:

Обозначение (пример): Р 5 /7

Р = 7 для расчета головки зуба,

Р = 5 для расчета других параметров.

Система обозначений и преобразований

Диаметр окружности выступов: OD = d_a.

Диаметр делительной окружности: PD = N/P = d (в дюймах) или PD = Nm = d (в мм).

Диаметр окружности впадин: RD = d_f

Начальный диаметр:

LD =(N+2x) / P (в дюймах)

или

LD= (N+2x)·m (в мм).

LD ≈ d_w,

где d_w — диаметральный модуль.

История

Сама по себе идея механической передачи восходит к идее колеса. Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.

В Древнем Египте для орошения земель уже использовались приводимые в действие быками устройства, состоявшие из деревянной зубчатой передачи и колеса с большим числом ковшей.

Вместо зубьев первоначально использовали деревянные цилиндрические или прямоугольные пальцы, которые устанавливали по краю деревянных ободьев.

Изготовленный в I веке до н.э. Антикитерский механизм состоял из десятков металлических зубчатых колес .

Важные замечания.

Смещение исходного контура при нарезке зубьев применяют для восстановления изношенных поверхностей зубьев колеса, уменьшения глубины врезания на валах-шестернях, для увеличения нагрузочной способности зубчатой передачи, для выполнения передачи с заданным межосевым расстоянием не равным делительному расстоянию, для устранения подрезания ножек зубьев шестерни и головок зубьев колеса с внутренними зубьями.

Различают высотную коррекцию ( x_Σ(d) =) и угловую ( x_Σ(d) ≠).

Смещение производящего контура на практике применяют обычно при изготовлении прямозубых колес и очень редко косозубых. Это обусловлено тем, что по изгибной прочности косой зуб прочнее прямого, а необходимое межосевое расстояние можно обеспечить соответствующим углом наклона зубьев. Если высотную коррекцию изредка применяют для косозубых передач, то угловую практически никогда.

Косозубая передача работает более плавно и бесшумно, чем прямозубая. Как уже было сказано, косые зубья имеют более высокую прочность на изгиб и заданное межосевое расстояние можно обеспечить углом наклона зубьев и не прибегать к смещению производящего контура. Однако в передачах с косыми зубьями появляются дополнительные осевые нагрузки на подшипники валов, а диаметры колес имеют больший размер, чем прямозубые при том же числе зубьев и модуле. Косозубые колеса менее технологичны в изготовлении, особенно колеса с внутренними зубьями.

Подписывайтесь на анонсы статей в окнах, расположенных в конце каждой статьи или вверху каждой страницы.

Прошу уважающих труд автора скачивать файл после подписки на анонсы статей!

Ссылка на скачивание файла: modul-zubchatogo-kolesa (xls 41,0KB).

Обозначения для расчёта шестерней по формулам.

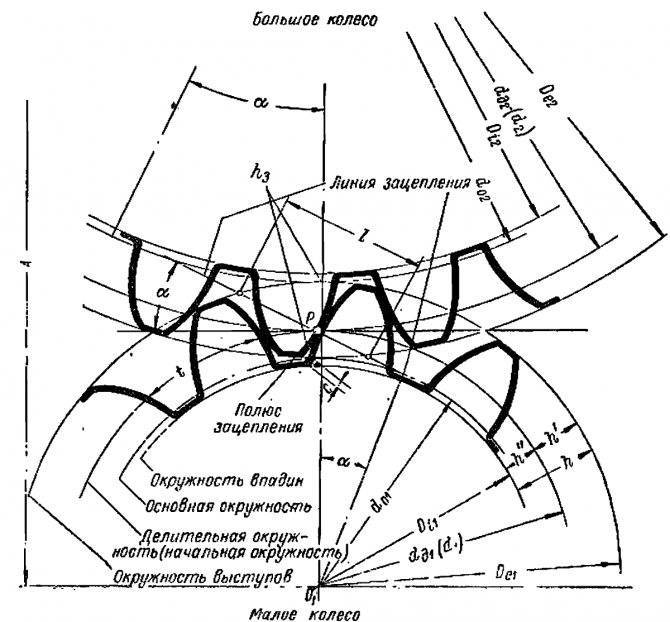
К вашему вниманию все обозначения какие вам понадобятся для расчета по формулам параметров шестерней. В данной таблице представлены основные обозначения параметров цилиндрических зубчатых колес:

• Высота зуба (полная).
• Высота головки зуба от окружности выступов до делительной окружности.
• Высота ножки зуба от делитель-ной окружности до окружности впадин.
• Глубина замера толщины зуба.
• Глубина захода зубьев, равная сумме высот головок зубьев (рабочая высота зуба).
• Диаметр начальной окружности.
• Диаметр делительной окружности.
• Диаметр основной окружности.
• Диаметр окружности выступов.
• Диаметр окружности впадин.
• Длина зацепления.
• Зазор радиальный в зубчатой паре.
• Зазор боковой в зубчатой паре.
• Зазор боковой в торцовом сечении.
• Зазор боковой в нормальном сечении.
• Коэффициент сдвига осей.
• Коэффициент высоты зуба инструмента (исходного контура).
• Коэффициент высоты зуба инструмента по отношению к модулю в нормальном, сечении.
• Коэффициент высоты зуба инструмента по отношению к модулю в торцовом сечении.
• Коэффициент сдвига исходного контура (инструмента).
• Коэффициент сдвига исходного контура (инструмента) минимальный при котором нет подрезания.
• Коэффициент сдвига исходного контура максимальный.
• Коэффициент сдвига исходного контура (инструмента) при заостренных зубьях.
• Коэффициент перекрытия.
• Коэффициент перекрытия в торцовой плоскости для косозубых колес.
• Модуль торцовый.
• Модуль нормальный.
• Межцентровое (межосевое) расстояние сцепляющейся пары колес.
• Межцентровое расстояние фаузацепления .
• Питч диаметральный.
• Питч окружной.
• Половина угловой толщины зуба на делительной окружности.
• Разность сдвигов—разность коэффициентов коррекции при внутреннем зацеплении.
• Сумма сдвигов исходного контура.
• Сумма коэффициентов коррекции сцепляющихся колес.
• Сумма чисел зубьев сцепляющихся колес при внутреннем зацеплении.
• Сумма чисел зубьев сцепляющихся колес при наружном зацеплении.
• Толщина зуба номинальная по хорде делительной окружности.
• Толщина зуба по дуге делительной окружности номинальная (без обязательного утонения) — для прямозубых колес.
• Толщина зуба номинальная по постоянной хорде для прямозубых колес.
• Толщина зуба номинальная по постоянной хорде для косозубых колес в нормальном сечении.
• Толщина зуба номинальная по постоянной хорде для косозубых колес в торцовом сечении.
• Толщина зуба по дуге окружности выступов.
• Толщина, зуба по постоянной хорде верхний предельный размер.
• Толщина зубьев по общей нормали для прямозубых колес .
• Толщина зубьев по общей нормали для прямозубых колес (или реек) — верхний предельный размер.
• Толщина зубьев по общей нормали для косозубых колес в нормальном сечении.
• Толщина зубьев по общей нормали для косозубых колес в нормальном сечении — верхний предельный размер.
• Угол зацепления пары колес.
• Угол зацепления косозубых колес в торцовом сечении.
• Угол инструмента профильный (исходного контура).
• Угол инструмента в нормальном сечении профильный.
• Угол инструмента в,торцовом сечении профильный.
• Угол наклона зубьев на основном цилиндре.
• Угол наклона зубьев на делительном цилиндре.
• Число зубьев.
• Число зубьев колеса, свободного от подрезания, минимальное.
• Число зубьев колеса практически допускаемое минимальное.
• Число зубьев, охватываемых размером.
• Шаг по делительной окружности.
• Шаг основной.
• Шаг торцовый.
• Шаг нормальный.
• Ширина зубчатого венца.

Заказ: Шестерня, диск. Модуль шесть.

Предыдущая запись

Исходный контур зубчатых колёс.

Следующая запись

Цилиндрические зубчатые колёса [ править | править код ]

Профиль зубьев колёс как правило имеет эвольвентную боковую форму. Однако существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.

Параметры эвольвентного зубчатого колеса:

m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб. Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:

>> >

• z — число зубьев колеса
• p — шаг зубьев (отмечен сиреневым цветом)
• d — диаметр делительной окружности (отмечена жёлтым цветом)
• d_a — диаметр окружности вершин тёмного колеса (отмечена красным цветом)
• d_b — диаметр основной окружности — эвольвенты (отмечена зелёным цветом)
• d_f — диаметр окружности впадин тёмного колеса (отмечена синим цветом)
• h_aP+h_fP — высота зуба тёмного колеса, x+h_aP+h_fP — высота зуба светлого колеса

В машиностроении приняты определённые значение модуля зубчатого колеса m для удобства изготовления и замены зубчатых колёс, представляющие собой целые числа или числа с десятичной дробью: 0,5; 0,7; 1; 1,25; 1,5; 1,75; 2; 2,5; 3; 3,5; 4; 4,5; 5 и так далее до 50. (подробнее см. ГОСТ 9563-60 Колеса зубчатые. Модули)

Высота головки зуба — h_aP и высота ножки зуба — h_fP — в случае т. н. нулевого зубчатого колеса (изготовленного без смещения, зубчатое колесо с «нулевыми» зубцами) (смещение режущей рейки, нарезающей зубцы, ближе или дальше к заготовке, причем смещение ближе к заготовке наз. отрицательным смещением, а смещение дальше от заготовки наз. положительным) соотносятся с модулем m следующим образом: h_aP = m; h_fP = 1,25 m, то есть:

h f P h a P = 1 , 25 >>>=1,25> >

Отсюда получаем, что высота зуба h (на рисунке не обозначена):

h = h f P + h a P = 2 , 25 m >+>=2,25m> >

Вообще из рисунка ясно, что диаметр окружности вершин d_a больше диаметра окружности впадин d_f на двойную высоту зуба h. Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр d_a и результат разделить на число зубьев z плюс 2:

m = d a z + 2 >> >

Продольная линия зуба

Зубчатые колеса классифицируются в зависимости от формы продольной линии зуба на:

17. Длина общей нормали цилиндрических прямозубых колес

Измерение толщины зубьев при длине общей нормали W имеет то преимущество перед измерением по постоянной хорде, что не требуется более точного изготовления зубчатых колес по наружному диаметру.

Для прямозубых колес без смещения

для колес со смешением (при коэффициенте смещения х)

здесь W’ — длина общей нормали цилиндрических прямозубых колес при m_n = 1. Значения W’ в зависимости от числа зубьев колеса и числа зубьев, охватываемых при измерении, указаны в таблице, приведенной ниже.

Дайна общей нормали W’ цилиндрических прямозубых колес при m_n = 1 мм