Кинетическая энергия пружины

Физика

3.4. Механическая энергия

3.4.2. Потенциальная энергия

Потенциальная энергия — это механическая энергия системы тел, определяемая их (или частей одного тела) взаимным расположением.

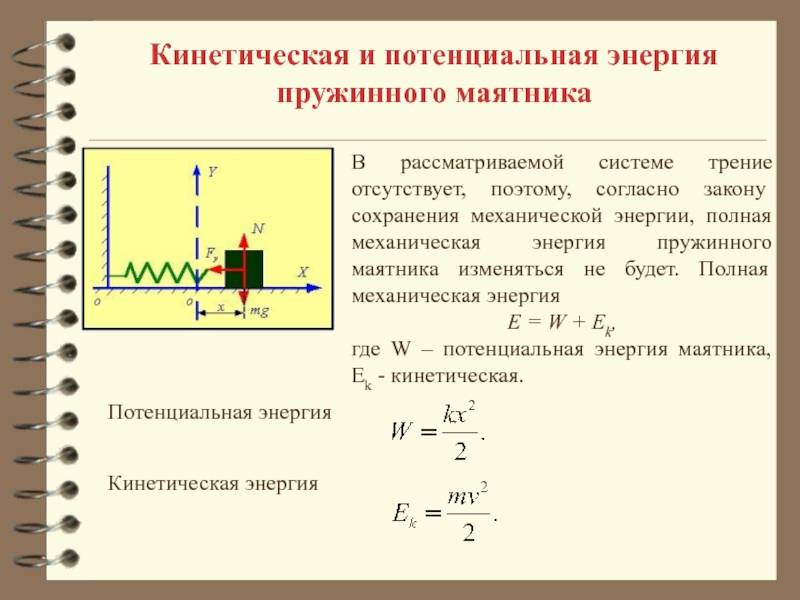
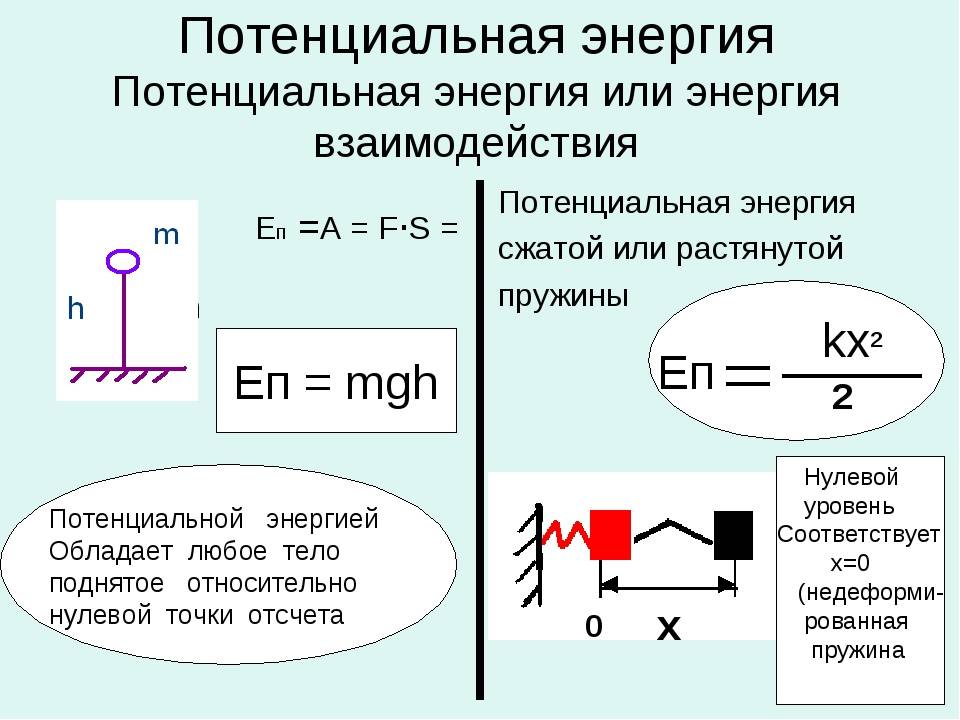
Потенциальная энергия деформированной пружины

Деформированная пружина (сжатая или растянутая) (рис. 3.7) обладает потенци­альной энергией, которая определяется формулой

W p = k ( Δ l ) 2 2 ,

где k — коэффициент жесткости (упругости) пружины; ∆l — величина абсолютной деформации пружины (удлинения или сжатия).

Рис. 3.7

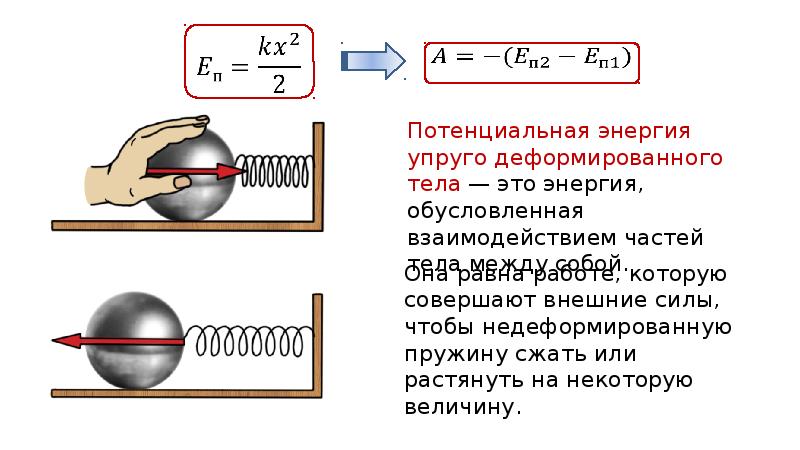
Потенциальная энергия недеформированной пружины равна нулю.

Следует отметить, что потенциальная энергия деформированной пружины всегда является положительной величиной.

В Международной системе единиц потенциальная энергия деформированной пружины измеряется в джоулях (1 Дж).

Потенциальная энергия взаимодействия тела и Земли

Тело, расположенное на расстоянии h над поверхностью Земли (или под ее поверхностью), обладает потенциальной энергией, которая определяется формулой

Wp = mgh + C,

где m — масса тела; g — модуль ускорения свободного падения.

Выбор константы C является условным и зависит от конкретной задачи; часто указанную константу выбирают таким образом, чтобы на поверхности планеты потенциальная энергия взаимодействия тела и планеты обращалась в ноль.

Следует отметить, что потенциальная энергия взаимодействия тела и Земли может быть как положительной, так и отрицательной величиной.

В Международной системе единиц потенциальная энергия тела, поднятого на некоторую высоту относительно поверхности Земли, измеряется в джоулях (1 Дж).

Пример 26. Две пружины с одинаковыми коэффициентами жесткости по 1,0 кН/м соединили последовательно. Составную пружину растянули на 10 см. Во сколько раз увеличится потенциальная энергия деформации, если эти же пружины соединить параллельно, а величину деформации системы оставить прежней? Рассчитать потенциальную энергию пружин при последовательном и параллельном соединении, считая деформацию составной пружины одинаковой и равной 10 см.

Решение. Потенциальная энергия составной пружины определяется формулой

W p = k общ ( Δ l ) 2 2 ,

где kобщ — общий коэффициент жесткости составной пружины; ∆l — величина деформации пружины.

Коэффициент жесткости составной пружины определяется по-разному:

для N одинаковых пружин, соединенных последовательно,

k общ 1 = k 0 N ;

для N одинаковых пружин, соединенных параллельно,

kобщ2 = Nk0,

где k0 — коэффициент жесткости одной пружины; N = 2 — количество соединенных пружин.

Потенциальная энергия составной пружины вычисляется по формулам:

для N одинаковых пружин, соединенных последовательно,

W p 1 = k общ 1 ( Δ l ) 2 2 = k 0 ( Δ l ) 2 2 N ;

для N одинаковых пружин, соединенных параллельно,

W p 2 = k общ 2 ( Δ l ) 2 2 = N k 0 ( Δ l ) 2 2 .

Отношение потенциальных энергий

W p 1 W p 2 = k 0 ( Δ l ) 2 2 N 2 N k 0 ( Δ l ) 2 = 1 N 2

определяется только количеством пружин и не зависит от деформации составной пружины.

Рассчитаем потенциальную энергию составной пружины, состоящей из двух одинаковых пружин,

соединенных последовательно:

W p 1 = k 0 ( Δ l ) 2 2 N = 1,0 ⋅ 10 3 ( 10 ⋅ 10 − 2 ) 2 2 ⋅ 2 = 2,5 Дж;

соединенных параллельно:

W p 2 = N k 0 ( Δ l ) 2 2 = 2 ⋅ 1,0 ⋅ 10 3 ( 10 ⋅ 10 − 2 ) 2 2 = 10 Дж.

Отношение указанных потенциальных энергий равно

W p 1 W p 2 = 1 N 2 = 1 2 2 = 4 .

Следовательно, при одинаковой деформации потенциальная энергия пружины, составленной из двух одинаковых параллельно соединенных пружин, в 4 раза больше потенциальной энергии пружины, составленной из двух одинаковых последовательно соединенных пружин.

Пример 27. Какой энергией обладает тело массой 500 г на вершине горы относительно дна озера, находящегося у подножия горы? Высота горы составляет 1,50 км, а глубина озера 250 м.

Решение. Потенциальная энергия тела, поднятого на некоторую высоту, определяется формулой

Wp = mgh,

где m — масса тела; g — модуль ускорения свободного падения; h — высота, на которую поднято тело над определенным уровнем, характеризуемым нулевым значением потенциальной энергии.

Выберем нулевой уровень потенциальной энергии (Wp = 0) на дне озера так, как показано на рисунке.

Тогда высота, на которую поднято тело над указанным уровнем, является суммой:

h = h2 + h2,

где h2 = 1,50 км — высота горы; h2 = 250 м — глубина озера.

Потенциальная энергия тела относительно дна озера определяется выражением

Wp = mg(h2 + h2).

Расчет дает значение:

W p = 500 ⋅ 10 − 3 ⋅ 10 ⋅ ( 1,50 + 0,25 ) ⋅ 10 3 = 8,75 ⋅ 10 3 Дж = 8,75 кДж.

Виды деформации

Деформация – это изменение формы, или размеров тела.

Есть несколько видов деформации:

• сдвиг;
• кручение;
• изгиб;
• сжатие/растяжение;

Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.

Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.

Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.

Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)

В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.

Что такое пружинный маятник

Пружинным маятником в физике называют систему, совершающую колебательные движения под действием силы упругости. 

Приняты следующие обозначения:

• m – масса тела;

• k – коэффициент жесткости пружины.

Общий вид маятника:

Особенностями пружинных маятников являются:

1. Сочетание тела и пружины. Массой пружины обычно в расчетах пренебрегают. Роль тела могут играть различные объекты. На них оказывают действие внешние силы. Груз может крепиться разными способами. Витки пружины, которыми она начинается и заканчивается, изготавливают с учетом повышенной нагрузки;

2. У любой пружины есть исходное положение, предел сжатия и растяжения. При максимальном сжатии зазора между витками нет. Когда она максимально растянута, возникает необратимая деформация;

3. Полная механическая энергия появляется с началом процесса обратимого деформирования. В этот момент на объект не оказывает действие сила упругости;

4. Колебательные движения происходят под влиянием силы упругости. Масштаб влияния определяется несколькими причинами (тип сплава, расположение витков и т. д.). Так как может происходить и сжатие и растяжение, можно сделать вывод, что сила упругости действует в двух противоположных направлениях;

5. От массы тела, величины и направления прикладываемой силы зависит скорость в плоскости его перемещения. Например, если подвесить груз к пружине и, растянув её, отпустить, то груз будет перемещаться в двух плоскостях: вертикально и горизонтально.

Теорема об изменении кинетической энергии

Опираясь на ранее приведенный пример, сформулируем теорему об изменении кинетической энергии тела, совершающего движение.

Теорема

Работа, произведенная в результате воздействия силы на определенное тело, эквивалентна изменениям его кинетической энергии. Это утверждение абсолютно применимо и к ситуации, когда на движущееся тело оказывается действие силы, с изменяющимся направлением и модулем.

\

Исходя из этого можно резюмировать, что показатель кинетической энергии тела с определенной массой(m), совершающего движение со скоростью \, соответствует значению работы, которую сила производит для разгона тела до данной скорости.

Дополнительные вопросы и задания

6. С высоты 20 м над поверхностью земли свободно без начальной скорости падает камень массой 300 г. За нулевой уровень потенциальной энергии камня примите уровень земли.

а) Чему равна потенциальная энергия камня в начальный момент? б) Чему равна потенциальная энергия камня через 1 с после начала движения?

в) Через какое время после начала движения потенциальная энергия камня уменьшилась в 2 раза по сравнению с ее начальным значением? 7. Шар массой 1 кг брошен с поверхности земли с начальной скоростью 20 м/с под углом 30º к горизонту. Считайте, что сопротивлением воздуха при движении шара можно пренебречь. а) До какой максимальной высоты поднялся шар?

None б) потенциальная энергия плота? 9. Когда сжатую пружину сжали еще на 2 см, ее потенциальная энергия увеличилась в 9 раз. а) Во сколько раз модуль конечной деформации пружины больше, чем модуль начальной деформации?

б) Чему равен модуль начальной деформации пружины? 10. Две пружины жесткостью 100 Н/м и 400 Н/м соединены последовательно. Систему соединенных пружин растянули на 5 см. а) Чему равна деформация более мягкой пружины? б) Чему равна деформация более жесткой пружины?

в) Потенциальная энергия упругой деформации какой пружины больше, и во сколько раз?

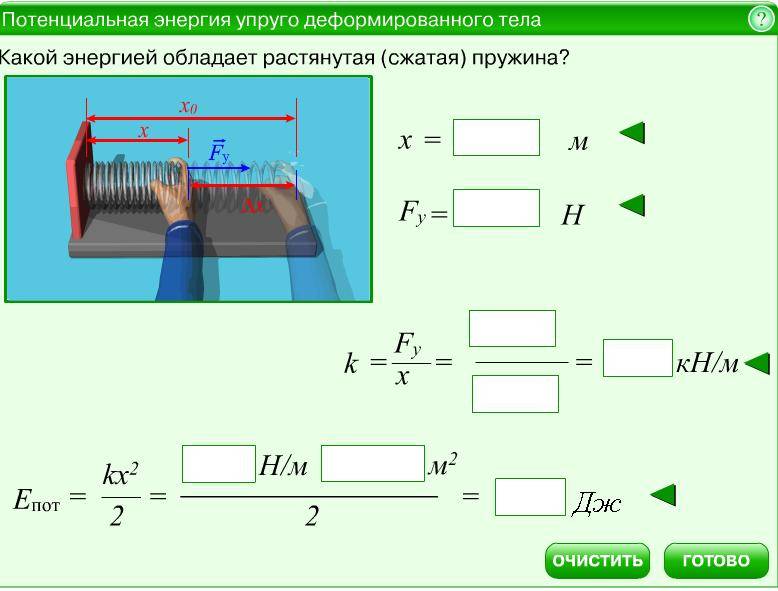
Деформированное упругое тело (например, растянутая или сжатая пружина) способно, возвращаясь в недеформированное состояние, совершить работу над соприкасающимися с ним телами. Следовательно, упруго деформированное тело обладает потенциальной энергией. Она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина, зависит от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к нерастянутому состоянию, т. е. найдем потенциальную энергию растянутой пружины. Пусть растянутая пружина закреплена одним концом, а второй конец, перемещаясь, совершает работу. Нужно учитывать, что сила, с которой действует пружина, не остается постоянной, а изменяется пропорционально растяжению. Если первоначальное растяжение пружины, считая от нерастянутого состояния, равнялось , то первоначальное значение силы упругости составляло , где — коэффициент пропорциональности, который называют жесткостью пружины. По мере сокращения пружины эта сила линейно убывает от значения  до нуля. Значит, среднее значение силы равно . Можно показать, что работа  равна этому среднему, умноженному на перемещение точки приложения силы: . Таким образом, потенциальная энергия растянутой пружины                                                                                  (98.1) Такое же выражение получается для сжатой пружины. В формуле (98.1) потенциальная энергия выражена через жесткость пружины и через ее растяжение . Заменив  на , где  — упругая сила, соответствующая растяжению (или сжатию) пружины , получим  выражение ,                                                                         (98.2) которое определяет потенциальную энергию пружины, растянутой (или сжатой) силой . Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, т.е. чем больше ее упругость, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной растягивающей, силе. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на перемещение точки приложения силы, т. е. работа. Эта закономерность имеет большое значение, например, при устройстве различных рессор и амортизаторов: при посадке на землю самолета амортизатор шасси, сжимаясь, должен произвести большую работу, гася вертикальную скорость самолета. В амортизаторе с малой жесткостью сжатие будет больше, зато возникающие силы упругости будут меньше и самолет будет лучше предохранен от повреждений. По той же причине при тугой накачке шин велосипеда дорожные толчки ощущаются резче, чем при слабой накачке.

Пружину можно назвать довольно распространенным изделием, которое применяется в самых различных случаях

Для правильного выбора пружины уделяется внимание проведению различных расчетов, некоторые из них предусматривает вычисление основных параметров, характеризующих работу. Потенциальная и кинетическая сила – два довольно распространенных показателя, которые касаются не только пружины, но и многих других тел

Рассмотрим особенности кинетической подробнее.

Задачи по теме с подробными решениями

Задача 1

Самолет, масса которого составляет 50 тонн, пролетает на высоте 10 километров. Скорость транспортного средства равна 900 км/ч. Требуется рассчитать, какова полная механическая энергия самолета.

Решение

Первым шагом является перевод искомых данных, согласно системе СИ. В таком случае масса самолета составит 50 000 кг, скорость – 250 м/с, а высота – 10 000 м.

Самолет обладает запасом полной энергии, которая включает и потенциальную, и кинетическую.

E = E_п + Е_к

E_п = m * g * h

Е_к = m * v2 / 2

Таким образом, полная энергия составит:

\(E=m\times g\times h\times \frac{mv^{2}}{2}\)

Если подставить в полученную формулу числовые значения величин из условия задачи, то получим полную энергию:

\(E=6.5625\times 10^{9}\) Дж

Если записать ответ сокращенно, то он примет такой вид:

\(Е = 6,5625\) Гдж.

Ответ: в рассмотренной системе отсчета значение полной механической энергии самолета составит 6.5625 Гдж.

Однако, данную задачу можно решить, принимая за нулевой уровень отметку в 10 километров. Тогда транспортное средство будет характеризоваться лишь запасом кинетической энергии, а значение потенциальной энергии будет равно нулю.

Задача 2

Пружину закрепили к стене и поместили на гладкую поверхность. На конце пружины зафиксировали тело. Растяжение пружины, которая обладает жесткостью в 400 Н/м, происходит при воздействии силы в 80 Н. Требуется рассчитать запас энергии в пружине.

Решение

Согласно условию задачи, поверхность обладает гладкостью, что позволяет сделать вывод о нулевом значении силы трения. Таким образом, потери энергии исключены. Воздействуя на пружину, можно наблюдать ее деформацию. Весь запас энергии будет сосредоточен в ней. Найти данную величину можно по формуле:

\(E=\frac{k(\Delta x)^{2}}{2}\)

Сила упругости равна произведению жесткости на изменение длины пружины:

\(k\times \Delta x=F\)

Деформацию пружины можно рассчитать таким образом:

\(\Delta x=\frac{F}{k}\)

Используя последнее равенство, можно преобразовать формулу для расчета энергии:

\(E=\frac{k(\frac{F}{k})^{2}}{2}=\frac{kF^{2}}{2k^{2}}=\frac{F^{2}}{2k}\)

Далее следует подставить числовые значения в полученное выражение:

\(E=\frac{80^{2}}{2\times 400}=8\) Дж

Ответ: запас энергии в пружине составляет 8 Дж.

Задача 3

Масса пули составляет 9 грамм. Ее выпустили из оружия вертикально в верхнем направлении. Скорость пули при этом составила 700 м/с. Требуется рассчитать ее кинетическую энергию.

Решение

Условия задачи удобно представить в виде рисунка.

Расчет нужно выполнить по формуле:

\(E=\frac{mv^{2}}{2}\)

Перед тем, как подставить в уравнение числовые значения, требуется перевести их в систему СИ. Тогда масса пули составит 0,009 кг. Выражение будет записано следующим образом:

\(E=\frac{0.009\times 49\times 10^{4}}{2}=2200\) Дж

Ответ: запас кинетической энергии пули равен 2200 Дж.

Задача 4

Масса ракеты составляет 0,2 кг. Ее выпустили из орудия вертикально вверх. После этого ракета достигла высоты в 60 метров. Требуется рассчитать значение потенциальной энергии ракеты, характерной для этой отметки.

Решение

Условие задачи можно представить с помощью рисунка.

Для того чтобы рассчитать потенциальную энергию, требуется воспользоваться формулой:

E = m * g * h

Далее необходимо подставить в выражение числовые значения:

Е = 0,2 * 9,8 * 60 = 118 Дж

Ответ: потенциальная энергия ракеты на заданной высоте составит 118 Дж.

Задача 5

Пружину растянули на 5 мм. Коэффициент ее жесткости составляет 10000 Н/м. Требуется вычислить, какова энергия пружины.

Решение

Следует представить условия задачи на рисунке.

Уравнение, с помощью которого можно рассчитать энергию пружины, имеет такой вид:

\(E=\frac{k(\Delta x)^{2}}{2}\)

Далее необходимо привести к системе СИ расстояние, на которое растянули пружину. Оно составит 0,005 м.

После преобразований можно подставить числовые значения в искомую формулу:

\(E=\frac{10^{4}\times 25\times 10^{-6}}{2}=0.125\) Дж

Ответ: энергия пружины составляет 0,125 Дж.

Знание основных формул для расчета кинетической, потенциальной и полной энергии тела позволит решить задачи любой сложности. Наиболее простым способом является выполнение последовательных действий, включая запись условий задачи, графическое изображение системы, представление формул для вычисления энергии, решение уравнения с помощью подстановки числовых значений

Важно отметить, что механическая энергия представляет собой сумму потенциальной и кинетической энергии

Максимальная кинетическая энергия груза на пружине

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.

Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:

В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:

Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .

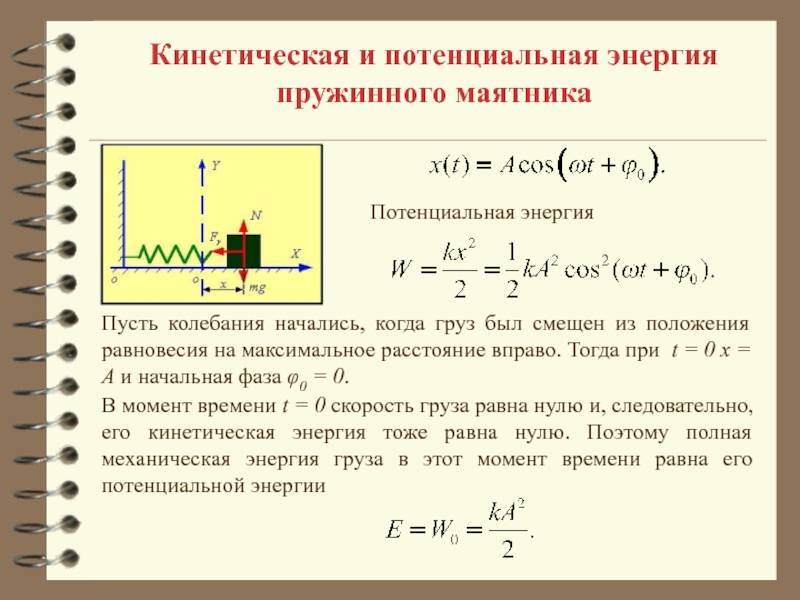
При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины.

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.

Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.

Для груза на пружине:

Запуск колебательного движения тела осуществляется с помощью кнопки Старт . Остановить процесс в любой момент времени позволяет кнопка Стоп .

Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени

Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия

Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k. Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.

Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

1) амплитуда колебаний скорости

2) циклическая частота колебаний

3) максимальная кинетическая энергия груза

4) период колебаний

А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле

Б) Для пружинного маятника известны формулы кинетической энергии

Пру­жин­ный ма­ят­ник, со­сто­я­щий из груза и лёгкой пру­жи­ны, со­вер­ша­ет ко­ле­ба­ния. В мо­мент, когда груз на­хо­дит­ся в край­нем по­ло­же­нии, его не­мно­го под­тал­ки­ва­ют вдоль оси пру­жи­ны в на­прав­ле­нии от по­ло­же­ния

рав­но­ве­сия. Как в ре­зуль­та­те этого из­ме­ня­ют­ся мак­си­маль­ная ки­не­ти­че­ская энер­гия груза ма­ят­ни­ка и ча­сто­та его ко­ле­ба­ний?

Для каж­дой ве­ли­чи­ны опре­де­ли­те со­от­вет­ству­ю­щий ха­рак­тер из­ме­не­ния:

3) не из­ме­ня­ет­ся

За­пи­ши­те в таб­ли­цу вы­бран­ные цифры для каж­дой фи­зи­че­ской ве­ли­чи­ны. Цифры в от­ве­те могут по­вто­рять­ся.

Мак­си­маль­ная ки­не­ти­че­ская энер­гия груза ма­ят­ни­ка

Ча­сто­та ко­ле­ба­ний ма­ят­ни­ка

Груз под­толк­ну­ли от по­ло­же­ния рав­но­ве­сия, от­ку­да сле­ду­ет, что ам­пли­ту­да ко­ле­ба­ний груза уве­ли­чит­ся. При этом уве­ли­чит­ся также и мак­си­маль­ная по­тен­ци­аль­ная энер­гия пру­жи­ны. По за­ко­ну со­хра­не­ния энер­гии, это при­ве­дет к уве­ли­че­нию мак­си­маль­ной ки­не­ти­че­ской энер­гии груза ма­ят­ни­ка.

Пе­ри­од и ча­сто­та пру­жин­но­го ма­ят­ни­ка за­ви­сят толь­ко от массы груза и жест­ко­сти пру­жи­ны. Таким об­ра­зом, при уве­ли­че­нии ам­пли­ту­ды ко­ле­ба­ний груза, ча­сто­та ко­ле­ба­ний ма­ят­ни­ка не из­ме­нит­ся.

Механическая энергия

Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.

Она представляет собой совокупность кинетической и потенциальной энергии. Кинетическая энергия — это энергия действия. Потенциальная — ожидания действия.

Представьте, что вы взяли в руки канцелярскую резинку, растянули ее и отпустили. Из растянутого положения резинка просто «полетит», как только вы ей позволите это сделать. В этом процессе в момент натяжения резинка обладает потенциальной энергией, а в момент полета — кинетической.

Еще один примерчик: лыжник скатывается с горы. В самом начале — на вершине — у него максимальная потенциальная энергия, потому что он в режиме ожидания действия (ждущий режим ), а внизу горы он уже явно двигается, а не ждет, когда с ним это случится — получается, внизу горы кинетическая энергия.

Кинетическая энергия

Еще разок: кинетическая энергия — это энергия действия. Величина, которая очевиднее всего характеризует действие — это скорость. Соответственно, в формуле кинетической энергии точно должна присутствовать скорость.

Кинетическая энергия Ек = (m*v^2)/2 Ек — кинетическая энергия m — масса тела v — скорость [м/с]

Чем быстрее движется тело, тем больше его кинетическая энергия. И наоборот — чем медленнее, тем меньше кинетическая энергия.

Задачка раз

Определить кинетическую энергию собаченьки массой 10 килограмм, если она бежала за мячом с постоянной скоростью 2 м/с.

Решение:

Формула кинетической энергии Ек = (m*v^2)/2

Подставляем значения

Ек = (10*2^2)/2 = 20 Дж

Ответ: кинетическая энергия пёсы равна 20 Дж.

Задачка два

Найти скорость бегущего по опушке гнома, если его масса равна 20 килограммам, а его кинетическая энергия — 40 Дж

Решение:

Формула кинетической энергии Ек = (m*v^2)/2

Выразим скорость:

v^2 = (2*Eк)/m

Подставляем значения

Ответ: гном бежал со скоростью 2 м/с.

Потенциальная энергия

В отличие от кинетической энергии, потенциальная чаще всего тем меньше, чем скорость больше. Потенциальная энергия — это энергия ожидания действия.

Например, потенциальная энергия у сжатой пружины будет очень велика, потому что такая конструкция может привести к действию, а следовательно — к увеличению кинетической энергии. То же самое происходит, если тело поднять на высоту. Чем выше мы поднимаем тело, тем больше его потенциальная энергия.

Потенциальная энергия деформированной пружины Еп = (k*x^2)/2 Еп — потенциальная энергия k — жесткость [Н/м] x — удлинение пружины

Потенциальная энергия Еп = mgh Еп — потенциальная энергия m — масса тела g — ускорение свободного падения [м/с^2] h — высота На планете Земля g ≃ 9,8 м/с^2

Задачка раз

Найти потенциальную энергию рака массой 0,1 кг, который свистит на горе высотой 2500 метров. Ускорение свободного падения считать равным 9,8 м/с^2.

Решение:

Формула потенциальной энергии Еп = mgh

Подставляем значения

Eп = 0,1 * 9,8 * 2500=2450 Дж

Ответ: потенциальная энергия рака, свистящего на горе, равна 2450 Дж.

Задачка два

Найти высоту горки, с которой собирается скатиться лыжник массой 65 килограмм, если его потенциальная энергия равна 637 кДж. Ускорение свободного падения считать равным 9,8 м/с^2.

Решение:

Формула потенциальной энергии Еп = mgh

Выразим высоту:

h = Eп/mg

Переведем 637 кДж в Джоули.

637 кДж = 637000 Дж

Подставляем значения

h = 637 000/(65 * 9,8) = 1000 м

Ответ: высота горы равна 1000 метров.

Задачка три

Два шара разной массы подняты на разную высоту относительно поверхности стола (см. рисунок). Сравните значения потенциальной энергии шаров E1 и E2. Считать, что потенциальная энергия отсчитывается от уровня крышки стола.

Решение:

Потенциальная энергия вычисляется по формуле: E = mgh

По условию задачи

m1 = m

h1 = 2h

m2 = 2m

h2 = h

Таким образом, получим, что

E1 = m*g*2h = 2 mgh,

а E2 = 2mgh,

то есть E1 = E2.

Ответ: E1 = E2.

Средняя кинетическая энергия

В большинстве случаев проводится высчитывание среднего значения. Этот показатель не учитывает то, в каких положениях сила упругости высокая и низкая. Для расчета применяется формула: F=kl/2.

В данном случае достаточно знать лишь удлинение, которое измеряется при использовании обычного инструмента. Что касается коэффициента, то он может варьировать в достаточно большом диапазоне, зависит от следующих моментов:

1. Диаметра витков. С увеличением этого показателя существенно повышается коэффициент жесткости, изделие часто используется для выполнения большой работы.
2. Толщины применяемой проволоки. Рассматриваемое изделие представлено проволокой, которая накручивается вокруг установленной оси.
3. Расстояния между отдельными витками. Как правило, они расположены относительно друг друга на определенном расстоянии, которое одинаковое. По этому признаку выделяют варианты исполнения, предназначенные для сжатия и растяжения.
4. Типа применяемого материала при изготовлении. Некоторые сплавы характеризуются достаточно высокой жесткостью, могут переносить незначительную деформацию.

Коэффициент самостоятельно рассчитать не нужно, он берется с определенных таблиц. Среднее значение часто высчитывается в случае решения математических задач, при проектировании применяются другие формулы.

Работа и потенциальная энергия тела, поднятого над Землей

Величина потенциальной энергии зависит от выбора нулевого уровня энергии. В поле тяготения Земли нулевым уровнем энергии обладает тело, находящееся на поверхности планеты.

Работа силы тяжести

Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком:

A = – ∆E_p = –(mgh – mgh) = mg(h – h)

Если тело поднимается, сила тяжести совершает отрицательную работу. Если тело падает, сила тяжести совершает положительную работу.

Пример №3. Шарик массой 100 г скатился с горки длиной 2 м, составляющей с горизонталью угол 30о. Определить работу, совершенную силой тяжести.

Сначала переведем единицы измерения в СИ: 100 г = 0,1 кг. Под действием силы тяжести положение тела относительно Земли изменилось на величину, равную высоте горки. Высоту горки мы можем найти, умножим ее длину на синус угла наклона. Начальная высота равна высоте горки, конечная — нулю. Отсюда:

A = mg(h – h) = 0,1∙10(2∙sin30o – 0) =2∙0,5 = 1 (Дж)

Потенциальная энергия протяженного тела

Работа силы тяжести

Потенциальная энергия протяженного тела выражается через его центр масс. К примеру, чтобы поднять лом длиной l и массой m, нужно совершить работу равную:

A = mgh

где h — высота центра массы лома над поверхностью Земли. Так как лом однородный по всей длине, его центр масс будет находиться посередине между его концами, или:

Отсюда работа, которую необходимо совершить, чтобы поднять этот лом, будет равна:

Лежавшую на столе линейку длиной 0,5 м ученик поднял за один конец так, что она оказалась в вертикальном положении. Какую минимальную работу совершил ученик, если масса линейки 40 г?

Переведем единицы измерения в СИ: 40 г = 0,04 кг. Минимальная работа, необходимая для поднятия линейки за один конец, равна:

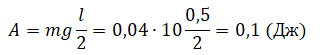
Работа и изменение потенциальной энергии упруго деформированного тела

Вспомним, что работа определяется формулой:

A = Fs cosα

Когда мы сжимаем пружину, шарик перемещается в ту же сторону, в которую направлена сила тяги. Если мы растягиваем ее, шарик перемещается так же в сторону направления силы тяги. Поэтому вектор силы упругости и вектор перемещения сонаправлены, следовательно, угол между ними равен нулю, а его косинус — единице:

Модуль силы тяги равен по модулю силе упругости, поэтому:

Перемещение определяется формулой:

s = x – x

Следовательно, работа силы тяги по сжатию или растяжению пружины равна:

Но известно, что потенциальная энергия упруго деформированного тела равна:

Следовательно, работа силы, под действием которой растягивается или сжимается пружина, равна изменению ее потенциальной энергии:

Энергия пружинного маятника

При рассмотрении колебания тел учитывают, что груз движется прямолинейно. Полная механическая энергия тела в каждой точке траектории является константой и равняется сумме его потенциальной энергии и кинетической энергии.

Потенциальная энергия:

Кинетическая энергия:

Полная энергия:

Расчет имеет особенности. При его проведении нужно учитывать несколько условий:

1. Колебания проходят в двух плоскостях: вертикальной и горизонтальной.
2. В качестве равновесного положения выбирается ноль потенциальной энергии. Находясь в этом положении пружина сохраняет свою форму.
3. Влияние силы трения при расчете не учитывают.

Формула определения жесткости

Изучаемая современными школьниками формула, как найти коэффициент жесткости пружины, представляет собой соотношение силы и величины, показывающей изменение длины пружины в зависимости от величины данного воздействия (или

равной ему по модулю силы упругости). Выглядит эта формула так: F = –kx. Из этой формулы коэффициент жесткости упругого элемента равен отношению силы упругости к изменению его длины. В международной системе единиц физических величин СИ он измеряется в ньютонах на метр (Н/м).

Другой вариант записи формулы: коэффициент Юнга

Деформация растяжения/сжатия в физике также может описываться несколько видоизмененным законом Гука. Формула включает значения относительной деформации (отношения изменения длины к ее начальному значению) и напряжения (отношения силы к площади поперечного сечения детали). Относительная деформация и напряжение по этой формуле пропорциональны, а коэффициент пропорциональности – величина, обратная модулю Юнга.

Модуль Юнга интересен тем, что определяется исключительно свойствами материала, и никак не зависит ни от формы детали, ни от ее размеров.

К примеру, модуль Юнга для ста

ли примерно равен единице с одиннадцатью нулями (единица измерения – Н/кв. м).

Смысл понятия коэффициент жесткости

Коэффициент жесткости – коэффициент пропорциональности из закона Гука. Еще он с полным правом называется коэффициентом упругости.

Фактически он показывает величину силы, которая должна быть приложена к упругому элементу, чтобы изменить его длину на единицу (в используемой системе измерений).

Значение этого параметра зависит от нескольких факторов, которыми характеризуется пружина:

• Материала, используемого при ее изготовлении.
• Формы и конструктивных особенностей.
• Геометрических размеров.

По этому показателю можно сд

елать вывод, насколько изделие устойчиво к воздействию нагрузок, то есть каким будет его сопротивление при приложении внешнего воздействия.

Особенности расчета пружин

Показывающая, как найти жесткость пружины, формула, наверное, одна из наиболее используемых современными конструкторами. Ведь применение эти упругие детали находят практически везде, то есть требуется просчитывать их поведение и выбирать те из них, которые будут идеально справляться с возложенными обязанностями.

Закон Гука весьма упрощенно показывает зависимость деформации упругой детали от прилагаемого усилия, инженерами используются более точные формулы расчета коэффициента жесткости, учитывающие все особенности происходящего процесса.

Например:

• Цилиндрическую витую пружину современная инженерия рассматривает как спираль из проволоки с круглым сечением, а ее деформация под воздействием существующих в системе сил представляется совокупностью элементарных сдвигов.
• При деформации изгиба в качестве деформации рассматривается прогиб стержня, расположенного концами на опорах.