Деформация кручения

Внутренний крутящий момент

Внутренние скручивающие моменты появляются под действием внешних крутящих моментов mi, расположенных в плоскостях, перпендикулярных к продольной оси бруса.

Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.

Величина крутящего момента в любом сечении вала определяется методом сечений: т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов mi, расположенных по одну сторону от рассматриваемого сечения.

Правило знаков внутренних скручивающих моментов: Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.

В технике наиболее широко используются валы круглого поперечного сечения.

Теория кручения круглых валов основана на следующих гипотезах:

1. поперечное сечение, плоское до деформации вала, остается плоским и после деформации;
2. радиусы, проведенные мысленно в любом поперечном сечении, в процессе деформации вала не искривляются.

Деформация кручения

Напряжения и деформации при кручении

Исследование отдельных участков и слоев цилиндрического бруса, нагруженного скручивающим (вращающим) моментом, дает основание полагать, что в поперечных сечениях этого бруса нормальные напряжения (направленные вдоль оси) отсутствуют, а возникают только касательные напряжения, модули которых расположены в плоскости исследуемого сечения. Этот вывод опирается и на гипотезу о не надавливании волокон, предполагающую, что если брус представить в виде многочисленных цилиндрических продольных волокон, то при деформациях разного рода эти волокна не оказывают друг на друга силового воздействия (не давят друг на друга). Как показали многочисленные опыты и исследования, эта гипотеза справедлива в определенном интервале деформаций, и погрешностями в расчетах, связанными с ее применением, можно пренебречь.

На рис. 1 видно, что абсолютный сдвиг сечения волокна а равен дуге аа1 , а сечения волокна b — дуге bb1 . Этот сдвиг (т. е. длины дуг) можно определить, зная угол φ закручивания исследуемого сечения относительно центральной оси: дуга аа1 = rφ ; дуга bb1 = Rφ , где: r — расстояние от волокна а до оси кручения, R — радиус сечения круглого бруса, φ — полный угол закручивания бруса.

Так как радиусы сечений при кручении бруса остаются прямыми (принятое предположение), то величина абсолютного сдвига сечения волокон прямо пропорциональна их расстоянию от оси кручения, т. е. чем дальше от оси расположено продольное волокно, тем сильнее сдвинется его сечение относительно центральной оси.

Чистый косой изгиб

Чистый косой изгиб в свою очередь сводится к двум чистым прямым изгибам во взаимно перпендикулярных плоскостях.
 

Чистый косой изгиб, в свою очередь, сводится к двум чистым прямым изгибам во взаимно перпендикулярных плоскостях.
 

При чистом косом изгибе поперечные силы отсутствуют. Для расчетов на прочность и жесткость практически безразлично, будет ли изгиб чистым или поперечным, так как влияние поперечных сил, как правило, не учитывают.
 

Рассмотрим случай чистого косого изгиба.
 

Что называется чистым косым изгибом и поперечным косым изгибом.
 

Косой изгиб В случае чистого косого изгиба в поперечном сечении возникают два внутренних силовых фактора: изгибающие моменты Mz и Му. При поперечном косом изгибе в поперечных сечениях бруса одновременно с изгибающими моментами возникают поперечные силы Qy и Qz. Однако влиянием касательных напряжений от поперечных сил Q в расчетах на прочность и жесткость обычно пренебрегают.
 

Определим предельные нагрузки при чистом косом изгибе и при внецентренном сжатии ( растяжении) на основе теории жестко-пластического тела.
 

Таким образом, внецентренное сжатие представляет собой совокупность чистого косого изгиба и осевого сжатия.
 

Таким образом, в общем случае внецентренного растяжения ( сжатия) получается сочетание чистого косого изгиба с центральным растяжением или сжатием.
 

Таким образом, в общем случае внецентрсшюго растяжения ( сжатия) получается сочетание чистого косого изгиба с центральным растяжением или сжатием.
 

В общем случае вне-цемтренного нагружения призматический стержень испытывает одновременную деформацию растяжения или сжатия и чистого косого изгиба.
 

В общем случае внецентренного нагру-жения призматический стержень испытывает одновременную деформацию растяжения или сжатия и чистого косого изгиба. Внутренние усилия в каждом поперечном сечении стержня приводятся к осевому продольному усилию NX P и двум изгибающим моментам My Pzp и Мг Рур, возникающим в главных центральных плоскостях инерции xz и ху стержня.
 

В общем случае внецентренного на-гружения призматический стержень испытывает одновременную деформацию растяжения или сжатия и чистого косого изгиба. Внутренние усилия в каждом поперечном сечении стержня приводятся к осевой продольной силе NX P и двум изгибающим моментам MU Pzp и Mz Рур, возникающим в главных центральных плоскостях инерции хг и ху стержня.
 

В общем случае вне-центренного нагружения призматический стержень испытывает одновременную деформацию растяжения или сжатия и чистого косого изгиба.
 

Случай косого изгиба, при котором в поперечном сечении бруса возникает лишь изгибающий момент, называется чистым косым изгибом. Если же в сечении действует, кроме того, поперечная сила, то имеется поперечный косой изгиб.
 

Основные понятия

Под изгибом детали понимают естественное или искусственное изменение формы. Этот процесс разделяется на две категории – плоский или косой. В первом случае ось детали сохраняет своё первоначальное положение, во втором происходит её изменение в горизонтальной или вертикальной плоскости.

Основным теоретическим положением, определяющим физические процессы, протекающие в результате изгиба, является закон Гука. Согласно ему величина деформации (изгиба), пропорциональна приложенной к этому телу силе. Для каждого из видов деформации разработан индивидуальный расчёт действующих характеристик.

Оценка степени влияния действующих факторов на деформацию осуществляется с помощью следующих показателей:

• площади поверхности подверженной деформации;
• длины детали;
• силы, воздействующие на конструкцию;
• модуль упругости (его абсолютный показатель);
• величина и характер изменения модуля длины в результате упругой деформации.

Одним из важных параметров считается потенциальная энергия деформации при изгибе. На основании этих параметров производят определение модуля Юнга. С его помощью рассчитывают скорость распространения продольной волны. Величина механического напряжения, при которой деформация тела всё ещё будет упругой, а сам объект способен восстановить первоначальную форму после снятия нагрузки, называется пределом упругости. При превышении допустимого значения этого параметра тело начнёт разрушаться. Этот предел называется прочностью. При оценке прочностных показателей применяют следующие предположения:

1. О постоянстве нормальных напряжений. Она определяет постоянство расстояний при возникновении напряжений изгиба.
2. Плоскости сечений. Оно называется гипотезой Бернулли. Сечения детали в спокойном положении находятся в плоском состоянии. После деформации они сохраняют первоначальную форму, но разворачиваются относительно некоторой линии. Она называется нейтральной осью.
3. Отсутствие давлений на боковые поверхности. Считается, что соседние волокна не оказывают давления друг на друга.

Перечисленные гипотезы позволяют оценить деформации сдвига и характер изгиба каждого слоя исследуемой детали. Это происходит в результате воздействия различных сил. Нагрузки вызывают деформацию изгиба в различных плоскостях. Они подразделяются на две категории:

• характеру воздействия (статические или динамические);
• степени воздействия (массовые или объёмные);
• поверхности (сосредоточенные, воздействуют на отдельные элементы поверхности и распределёнными – на всю поверхность).

К статическим относятся нагрузки, у которых место приложения и направления сил не меняется или изменяются медленно в течение определённого промежутка времени. К таким нагрузкам относится сила тяжести. В этом случае можно принять утверждение, что элементы физического объекта находятся в состоянии равновесия. У динамических нагрузок эти параметры меняются достаточно быстро или носят импульсивный характер. К ним относятся ударные нагрузки при забивании свай, обработке металла ковкой, воздействие неровностей дороги на колесо.

При сосредоточенной статической нагрузке на отдельный участок поверхности бруса происходит его деформация в сторону по направлению сил взаимодействия. Для расчёта параметров характеризующих основные показатели состояния деформированного тела применяют дифференциальные уравнения, которые позволяют выявить существующие функциональные связи. По деформации изгиба с помощью модуля Юнга можно вычислить прочность исследуемого элемента конструкции (балки, бруса, подвесной опоры и т. д.). На основании полученных областей решения можно построить графическое изображение силы упругости, которое наглядно показывает, что происходит с различными участками деформированной детали. Для каждой детали в зависимости от её геометрических размеров, материала изготовления и величины приложенных сил выведена своя формула.

Для наглядности восприятия характера протекающих процессов использует метод нанесения эпюр на поверхность объекта. Эта операция называется топология. Основной идеей является проецирование линий нагрузки на соответствующую плоскость (горизонтальную, фронтальную или профильную). В современных методах топологии применяют фрактальную геометрию.

Изгибающий момент и поперечная сила

Для оценки параметров деформационных процессов, протекающих в различных конструкциях, применяют изгибающий момент и воздействующую поперечную силу. Их рассчитывают на основании уравнений равновесия. Каждое позволяет найти параметры каждого слоя балки при изгибе.

При проектировании конструкции для расчёта этих параметров учитывают следующие правилами:

• воздействие внешнего фактора, способного повернуть балку по часовой стрелке относительно проведенного сечения;
• создаётся изгибающий момент, способный привести к сжатию каждого из волокон балки (в уравнении его учитывают со знаком плюс);

Полученные результаты позволяют построить графическое изображение распределения сил и моментов на различных уровнях. Такие изображения называют эпюрами. С их помощью определяют прочность создаваемой конструкции.

Эпюры для двухопорных балок

Рассматривая расчетные схемы такого типа, как двухопорная балка (рис. 5),

Рис. 5

необходимо вначале найти опорные реакции и только потом строить эпюры.

Определим реакции в обеих опорах, для этого используем два независимых уравнения статики, т.к. у нас плоская система параллельных сил.

Обычно, рекомендуется использовать суммы моментов вокруг опорных точек, например: ∑M_A=0 и ∑M_B=0.

Записываем уравнения и находим значения реакций:

_YС

Проверим через сумму сил, приложенных к балке (включая найденные опорные реакции). Она должна равняться нулю (при округлении значений, может появиться погрешность).
Для построения эпюр рассмотрим два силовых участка:

Рис. 6

I участок (AC): 0 ≥ z₁ ≥2a (рис. 6, а, г)
Q(z₁)=R_A-qz₁ — прямая, которую строим по двум граничным точкам:
M(z₁)=R_Az₁-qz₁(z₁/2)= R_Az₁-qz₁2/2 – парабола.

Строим эту кривую по трем точкам: по двум граничным (0 и 2a) и z*, которая соответствует M_max(z*), и дифференциальной зависимости:Определяем экстремум эпюры M на участке:

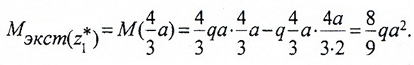_22B2B2221111

II силовой участок: 0 ≥ z₂ ≥ a.
следовательно, q=0.
функция M(z) – убывающая.
Все проверки выполнены, следовательно, эпюры построены верно.
По эпюрам видно, что опасных сечений два (рис. 6):
По моменту при z₁*=4/3a
По силе в сечении «A»
После построения и проверки эпюр можно приступать к расчетам балки на прочность и жесткость.

Подробные примеры построения эпюр >Лекции по сопромату >Примеры решения задач >

Расчёты на прочность при изгибе

Особую важность при проектировании конструкций и их отдельных элементов играют предварительные расчёты на прочность при возникающих изгибах. По результатам проведенных расчётов устанавливают фактические (реальные) и допустимые напряжения, которые способны выдержать элементы и вся конструкция в целом. Это позволит определить реальный срок службы разработать рекомендации по правильной эксплуатации разработанного объекта

Это позволит определить реальный срок службы разработать рекомендации по правильной эксплуатации разработанного объекта.

Условие прочности выводится в результате сравнения двух показателей. Наибольшего напряжения, которое возникает в поперечном сечении при эксплуатации и допустимого напряжения для конкретного элемента. Прочность зависит от применённого материала, размера детали, способа обработки и его физико-механических и химических свойств.

Для решения поставленной задачи применяются методы и математический аппарат, разработанный в дисциплинах техническая механика, материаловедение и сопротивление материалов. В этом случае применяются:

• дифференциальные зависимости Журавского (семейство дифференциальных уравнений связывающие основные параметры при деформации и их производные);
• способы определения перемещения (наиболее эффективными считаются метод Мора и правило Верещагина);
• семейство принятых гипотез;
• разработанные правила построения графических изображений (построение эпюр).

Расчёт параметров производится в три этапа:

• при проверочном расчёте (вычисляют величину максимального напряжения);
• на этапе проектирования (производится выбор толщины и параметров сечения бруса);
• во время вычисления допустимой нагрузки.

Полученные знаки величин напряжений определяются на основании оценки протекающих физических процессов и направления проекций векторов сил и моментов.

Наиболее наглядными результатами расчёта являются построенные эпюры на поверхности разрабатываемого изделия. Они отражают влияние всех силовых факторов на различные слои деталей. При чистом изгибе эпюры имеют следующие особенности:

• на участке исследуемой балки с отсутствием нагрузки, которая носит распределённый характер, эпюра изображается прямой линией;
• на участке приложения так называемых сосредоточенных сил на эпюре наблюдается изменение направления в форме скачка в том месте к которому приложен вектор силы;
• в точке появления приложенного момента, скачок равен величине этого параметра;
• на участке с распределённой нагрузкой интенсивность воздействия изменяется по линейному закону, а поперечные нагрузки носят степенной характер изменения (чаще всего по параболической кривой, с направлением выпуклости в сторону приложенной нагрузке);
• в границах исследуемого участка функция изгибающего момента приобретает экстремум (на основании методов исследования функций с помощью дифференциального исчисления можно установить характер экстремума – максимум или минимум).

На практике решение систем дифференциальных уравнений может вызвать определённые трудности. Поэтому при расчётах допускаются некоторые прощения, которые не влияют на точность определяемых параметров. К этим упрощениям относятся:

• расчёт производят с учётом нормальных напряжений;
• в качестве основного предположения принимают гипотезу о плоских сечениях;
• продольные волокна не производят дополнительного давления между собой (это позволяет считать, что процессы изгиба носят линейный характер);
• деформация волокон не зависит от их ширины (значения нормальных напряжений постоянные по всей ширине);
• для расчётной балки задают одну плоскость симметрии (все внешние силы лежат в этой плоскости);
• физико-механические характеристики материала подчиняются закону Гука (модуль упругости имеет постоянную величину);
• процессы в балке подчиняются законам плоского изгиба (это допущение вытекает из соотношений геометрических размеров изделия).

Современные методы исследования воздействия внешних сил, внутренних напряжений и моментов позволяют с высокой степенью точности рассчитать прочность каждой детали и всей конструкции в целом. Применение компьютерных методов расчёта, фрактальной геометрии и 3D графики позволяет получить подробную картину происходящих процессов.

Определение и общие сведения о деформации сдвига

Основным признаком, характеризующим деформацию сдвига, является сохранение постоянства объёма. Не зависимо от того, в каком направлении действуют силовые факторы этот параметр остаётся неизменным.

Примеры проявления деформации сдвига можно обнаружить при проведении различного рода работ. К таким случаям относятся:

• при распиловке бруса;
• отрезание или рубка металла;
• в результате нарушения целостности крепления металлических или деревянных деталей, соединённых метизами;
• балки в местах крепления опор;
• места скрепления мостовых пролётов;
• крепёж на перемычках соединения железнодорожных рельс;
• разрезания листа бумаги ножницами.

При определённых условиях наблюдается чистый сдвиг. Он определяется как сдвиг, при котором на все четыре грани (например, прямоугольной детали) оказывают воздействие только напряжения, направленные по касательной к поверхности. В этом случае произойдёт плавный сдвиг всех слоёв детали от верхних к нижним слоям. Тогда внешняя сила изменяет форму детали, а объём сохраняется.

Для оценки величины сдвига и надёжности конструкции используют следующие параметры:

• величина, направление и точка приложения воздействующей силы;
• модуль сдвига;
• угол изменения внешних граней изделия;
• тангенциальное напряжение;
• модуль кручения (зависит от физико-механических характеристик материала);

Расчёт и практическое измерение этих параметров необходимы для оценки устойчивости и целостности конструкции. Формула, позволяющая вычислить допустимые изменения, учитывает все воздействия на конкретные слои детали и всю конструкции в целом.

В случае воздействия деформации величина угла считается пропорциональной внешней силе. Увеличение степени воздействия может превратить деформацию сдвига в срез. Это приведёт к разрушению не только элементов крепления (болтов, шпилек, заклёпок), но и всей детали.

Для наглядности изменения формы детали при деформации сдвига динамика процесса обозначается с помощью величины угла смещения и векторов возникающих напряжений. Действующая сила направлена в сторону смещения слоёв рассматриваемой детали.

В современных условиях угол сдвига измеряется различными техническими приборами. Основным прибором для измерения параметров смещения является тензомер. Эти приборы работают на различных физических принципах:

• оптические (в том числе лазерные);
• акустические;
• рентгеновские; электрические;
• пневматические.

В этих приборах относительная деформация сдвига обрабатывается на современных вычислительных средствах с применением соответствующего программного обеспечения. Каждый метод обладает своими достоинствами и недостатками. Их применение зависит от поставленной задачи, технической и финансовой возможности.

Сжатие и растяжение

Деформация растяжения связана с относительным либо абсолютным удлинением тела. В качестве примера можно привести однородный стержень, который закреплен с одного конца. При приложении вдоль оси силы, действующей в противоположном направлении, наблюдается растягивание стержня.

Сила же, прикладываемая по направлению к закрепленному концу стержня, приводит к сжатию тела. В процессе сжатия либо растяжения происходит изменение площади сечения тела.

Деформация растяжения – это изменения состояния объекта, сопровождающиеся смещением его слоев. Данный вид можно проанализировать на модели твердого тела, состоящего из параллельных пластин, которые между собой соединены пружинками. За счет горизонтальной силы осуществляется сдвиг пластин на какой-то угол, объем тела при этом не меняется. В случае упругих деформаций между силой, приложенной к телу, и углом сдвига выявлена прямо пропорциональная зависимость.

Подведём итоги

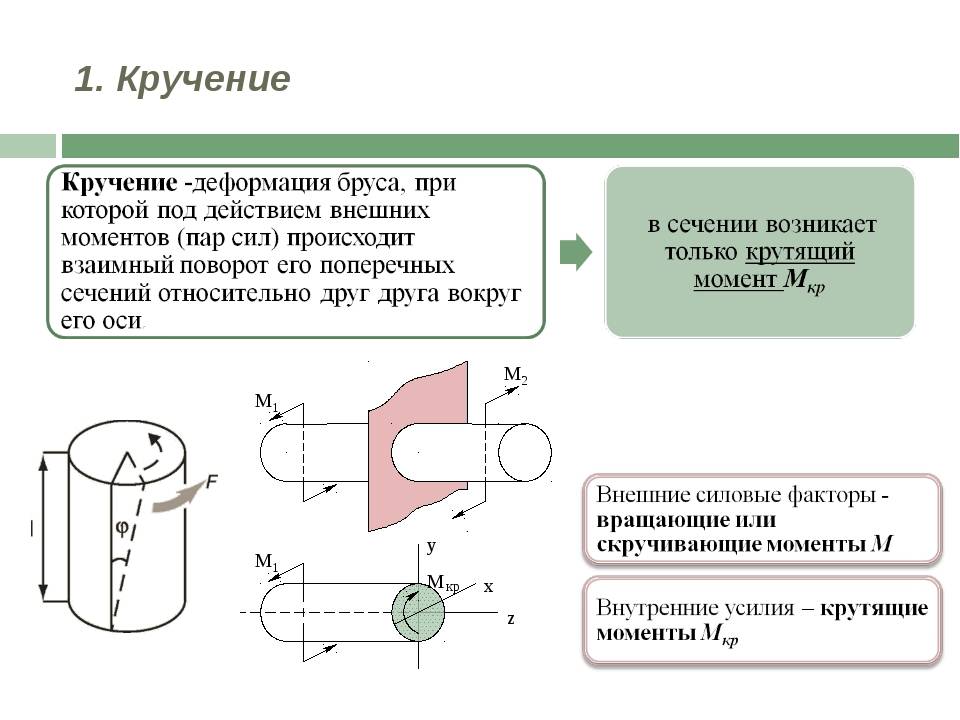
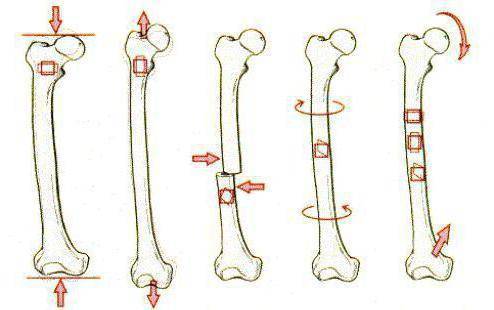
Кручение — такой вид деформации стержня, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент.

Стержни, испытывающие кручение, принято называть валами.

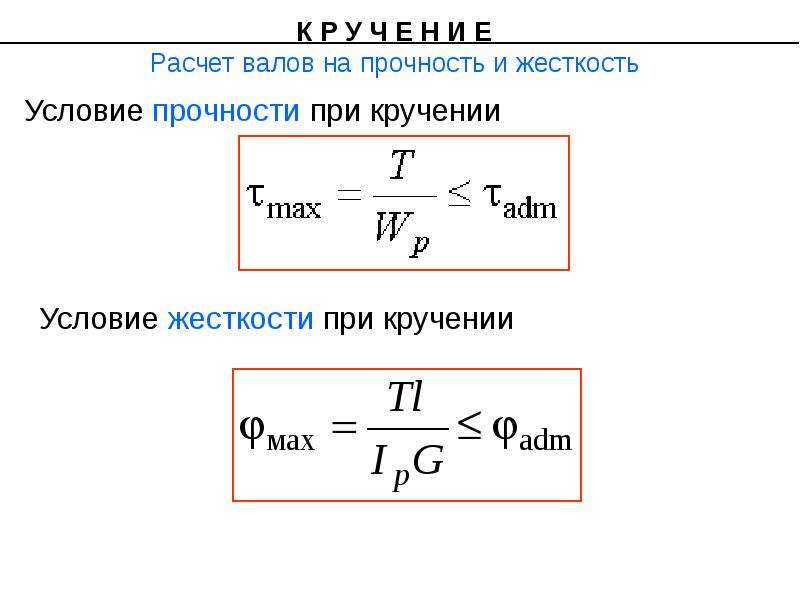
При чистом кручении (которое почти не встречается в реальной жизни) стрежень испытывает только касательные напряжения. Они достигают максимума у краёв сечения и равны:

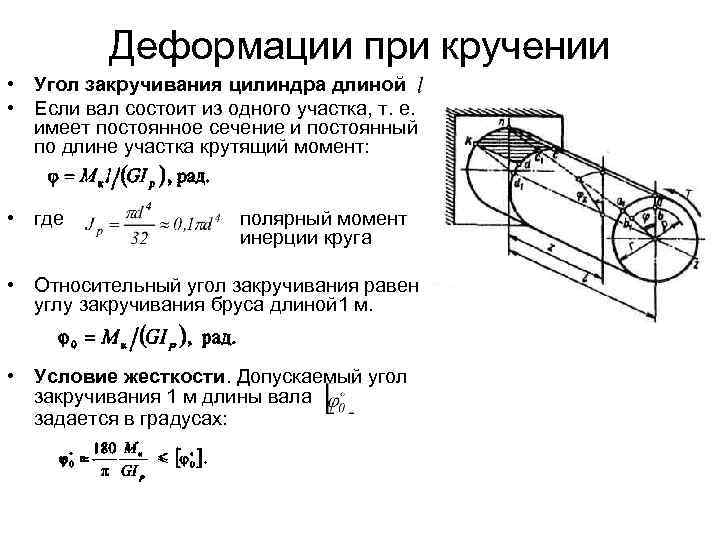
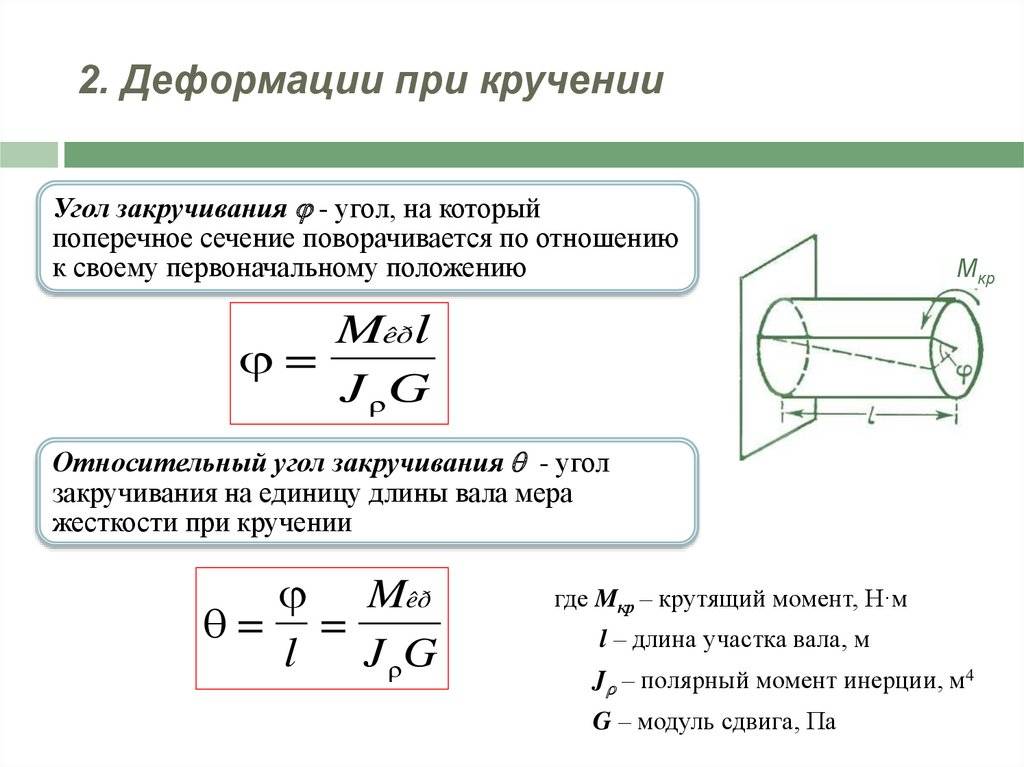
Под действием нагрузки стержень деформируется. Деформация при чистом кручении – угол поворота. Абсолютный угол поворота (для всего стержня) определяется по формуле:

Расчёт стержней проводится для двух предельных состояний – потери прочности (разрушения) и слишком высоких деформаций.

Напоследок – спойлер к следующим статьям. Как, по мнению читателя, рассчитать балку, если на неё действует вертикальная распределённая нагрузка, но ВНЕЦЕНТРЕННО? Как учесть кручение от поперечного сечения от такой нагрузки? Поговорим в следующих статьях!

Библиографический список

1. Александров, А.В. Сопротивление материалов: учебник/А.В. Александров, В.Д. Потапов, Б.П. Державин.– 3-е изд., испр. – М.: Высшая шк., 2003. – 560 с.

2. Андреев, В.И. Техническая механика (для учащихся строительных вузов и факультетов): учебник/ В.И. Андреев, А.Г. Паушкин, А.Н. Леонтьев. – М.: Издательство АСВ, 2012. – 251с.

3. Варданян, Г.С. Сопротивление материалов (с основами строительной механики): учебник/ Г.С. Варданян, Н.М. Атаров, А.А. Горшков. – М.: ИНФА-М, 2003. – 480 с. 

4. Сопротивление материалов: учебник / А. Ф. Смирнов, А. В. Александров, Н. И. Монахов и др. – 3-е изд., перераб. и доп. – М.: Высшая шк., 1975. – 480 c.

5. Беляев, Н.М. Сопротивление материалов: учебник/ Н.М. Беляев. – М.: Наука, 1976. – 608 с. 6. Рудицын, М.Н. Справочное пособие по сопротивлению материалов/ М.Н. Рудицын, П.Я. Артемов, М.И. Любошиц. – 3-е изд., перераб. и доп. – Минск, Вышэйшая шк., 1970. – 630 с.

6. Лекции ВГТУ, лекция №9 – Простые виды сопротивления. Кручение: . URL:http://sopromat.vstu.ru/metod/lek/lek_09.pdf (Дата обращения — 15.06.2022)

3 982