9.2. Последовательность выполнения чертежей деталей
Чертёж детали – это документ, содержащий изображение детали и другие данные, необходимые для её изготовления и контроля.Перед выполнением чертежа необходимо выяснить назначение детали, конструктивные особенности, найти сопрягаемые поверхности. На учебном чертеже детали достаточно показать изображение, размеры и марку материала.При выполнении чертежа детали рекомендуется следующая последовательность:
- Выбрать главное изображение (см. ).
- Установить количество изображений – видов, разрезов, сечений, выносных элементов, которые однозначно дают представление о форме и размерах детали, и дополняющих какой-либо информацией главное изображение, помня о том, что количество изображений на чертеже должно быть минимальным и достаточным.
- Выбрать масштаб изображений по ГОСТ 2.302-68. Для изображений на рабочих чертежах предпочтительным является масштаб 1:1. Масштаб на чертеже детали не всегда должен совпадать с масштабом сборочного чертежа. Крупные и не сложные детали можно вычерчивать в масштабе уменьшения (1:2; 1:2,5; 1:4; 1:5 и т.д.), мелкие элементы лучше изображать в масштабе увеличения (2:1; 2,5:1; 4:1; 5:1; 10:1; и т.д.).
- Выбрать формат чертежа. Формат выбирается в зависимости от размера детали, числа и масштаба изображений. Изображения и надписи должны занимать примерно 2/3 рабочего поля формата. Рабочее поле формата ограничено рамкой в строгом соответствии с ГОСТ 2.301-68* по оформлению чертежей. Основная надпись располагается в правом нижнем углу (на формате А4 основная надпись располагается только вдоль короткой стороны листа);
- Выполнить компоновку чертежа. Для рационального заполнения поля формата рекомендуется тонкими линиями наметить габаритные прямоугольники выбранных изображений, затем провести оси симметрии. Расстояния между изображениями и рамкой формата должно быть примерно одинаковым. Оно выбирается с учётом последующего нанесения выносных, размерных линий и соответствующих надписей.
- Вычертить деталь. Нанести выносные и размерные линии в соответствии с ГОСТ 2.307-68. Выполнив тонкими линиями чертёж детали, удалить лишние линии. Выбрав толщину основной линии, обвести изображения, соблюдая соотношения линий по ГОСТ 3.303-68. Обводка должна быть чёткой. После обводки выполнить необходимые надписи и проставить числовые значения размеров над размерными линиями (предпочтительно размером шрифта 5 по ГОСТ 2.304-68).
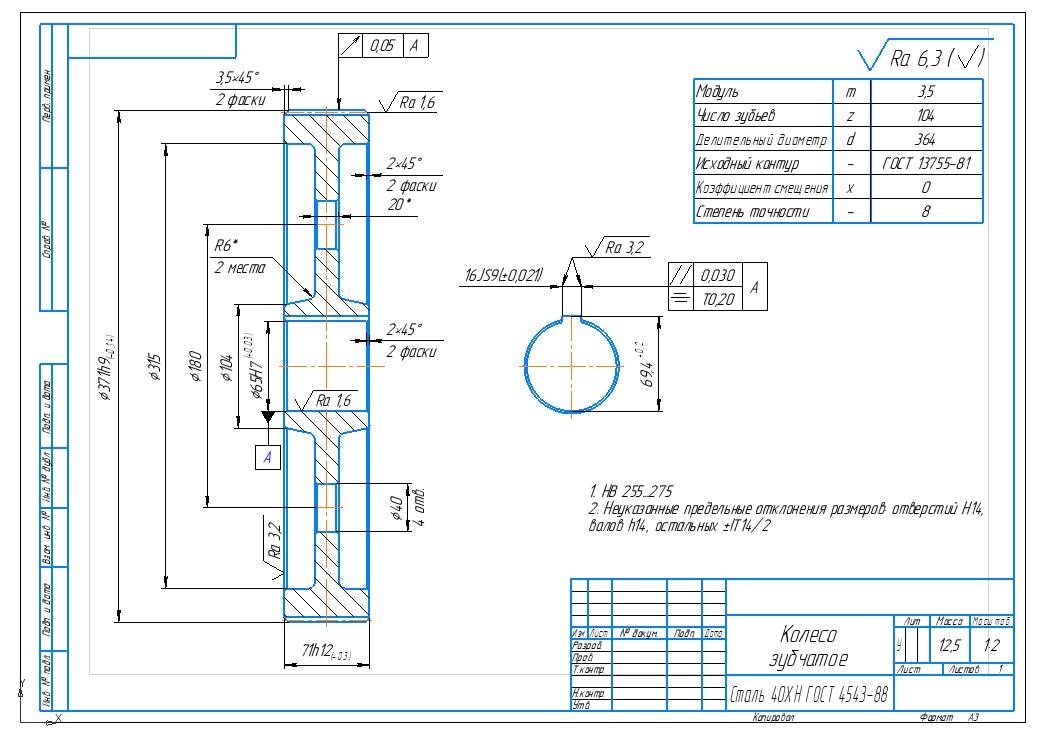
- Заполнить основную надпись. При этом указать: наименование детали (сборочной единицы), материал детали, её код и номер, кем и когда был выполнен чертёж и т.д. (Рисунок 9.1)
Ребра жесткости, спицы при продольных разрезах показывают не заштрихованными.Рисунок 9.1 – Рабочий чертеж детали «Корпус»
Конические зубчатые колеса (шестерни):
Конические зубчатые колеса используются в передачах, где оси валов пересекаются либо перекрещиваются. Данный тип колес так же широко применяется в машиностроении. Конические зубчатые колеса позволяют решать многие конструкторские задачи, часто встречающиеся в разработке сложных механизмов.

Рис. 2. Конические зубчатые колеса
Различают множество видов конических зубчатых колес.
Колесо с прямыми зубьями. Данная деталь имеет зубья прямой формы, теоретические линии которых проходят через конусную вершину. Данный вид является наиболее простым по технологии изготовления. Прямозубые конические колёса используют при низких окружных скоростях. Передача с такими колесами обеспечивает передаточное отношение до 3.
Колесо с тангенциальными зубьями. Такое колесо имеет прямые зубья, теоретические линии которых расположены касательно к окружности. У данного вида колеса угол спирали различен для различных точек линии зуба. Угол спирали в средней точке зубчатого венца выступает в качестве величины, которая характеризует наклон зубьев.
Колесо с криволинейными зубьями. Такой вид колес имеет ряд преимуществ, среди которых выделяются: мягкий вход, наименьший шум при работе, наибольшая нагрузка и большие окружные скорости. Данный вид передачи встречается среди видов, перечисленных ниже.
Колесо с круговыми зубьями. В данном виде шестерни зубья нарезаны в виде дуги по окружности с определенным углом наклона, который называют углом спирали. Такие шестерни мягко входят в зацепление, вследствие чего издают минимум шума. Они отличаются большей прочностью и допустимостью больших отклонений при установке.
Колесо с нулевым углом наклона зубьев. Такое изделие представляет собой колесо с круговыми зубьями, угол наклона зубьев которого в одной из точек делительной средней линии зуба равняется нулю. Колеса с нулевым наклоном зубьев еще называют «Зерол». Данный вид колес в своей работе дает минимальные осевые нагрузки и широко применяется в передачах с большими скоростями, в том числе в авиастроении, поскольку скорость у них может достигать более 7 метров в секунду. Колеса с нулевым наклоном зубьев могут заменять передачи, в которых были установлены прямозубые шестерни.
Колесо с эвольвентной линией зубьев. В данном типе шестерни при развертке конической основы зубья будут иметь тип эвольвенты основной окружности. Передача зубьев дает непрерывный крутящий переход, который исключает возможность проскальзывания.
Колесо с прямыми зубьями кругового профиля. Данный вид колес имеет профиль зубьев приблизительно круглой формы, у которых поверхность боковин выполнена огибанием рабочей части инструмента, и совершает движение в плоскости по кругу оси инструмента, а также производит поступательное движение мимо зубьев данного типа колеса. Колеса с прямыми зубьями кругового профиля также называют колесом Ривасайкл.
Колесо с круговыми зубьями, образованными сферой. Данное колесо имеет форму зуба, образованную при помощи зацепления на станке поверхностью сферической формы. Колесо также отличается повышенной бесшумностью, плавностью хода и более высокой окружной скоростью.
Плоское колесо. У данного вида колес угол делительного конуса является 90 градусов.
Примечание: Фото https://www.pexels.com, https://pixabay.com
Найти что-нибудь еще?
карта сайта
Коэффициент востребованности 1 367
Основные параметры зубчатого колеса
Создавать рассматриваемую конструкцию следует исключительно при заблаговременном создании чертежа, на котором отображаются основные параметры зубчатого колеса. Стоит отметить, что по создаваемой схеме некоторых механизмов также можно определить неправильный выбор основных параметров. В большинстве случае также делается упрощенный чертеж вала, за счет чего можно сразу определить принцип действия механизма.
Основными параметры, которые относятся к зубчатым колесам, являются:
- Делительная окружность пары зубчатых колес. Данный показатель применяется в случае проектирования зубчатой пары самого различного типа. Она определяется соприкасающимися окружностями, которые катаются одна по другой без скольжения. Применяется для обозначения момента зацепления и сопряжения. Для обозначения на чертеже применяется буква d. Стоит учитывать, что само обозначение зачастую не проставляется, а только указывается соответствующий размер.
- Окружный шаг зубьев. Этот параметр применяется для определения расстояния между отдельными профильными поверхностями соседних зубьев. Подобный показатель вычисляется путем разделения значения делительной окружности на число зубьев.
- Число зубьев. Достаточно важным моментом назовем то, что на чертеже не проводится отображение всех зубьев. В некоторых случаях проводится создание эскиза нескольких зубьев. За счет этого существенно упрощается поставленная задача по созданию рассматриваемого документа.
- В создаваемой таблице в обязательном порядке указывается число зубьев. Подобная информация позволяет проводить расчеты и определение других наиболее важных параметров.
- Длина делительной окружности.
- Основные геометрические параметры зуба. Основной частью зубчатых колес является именно зуб. Он применяется
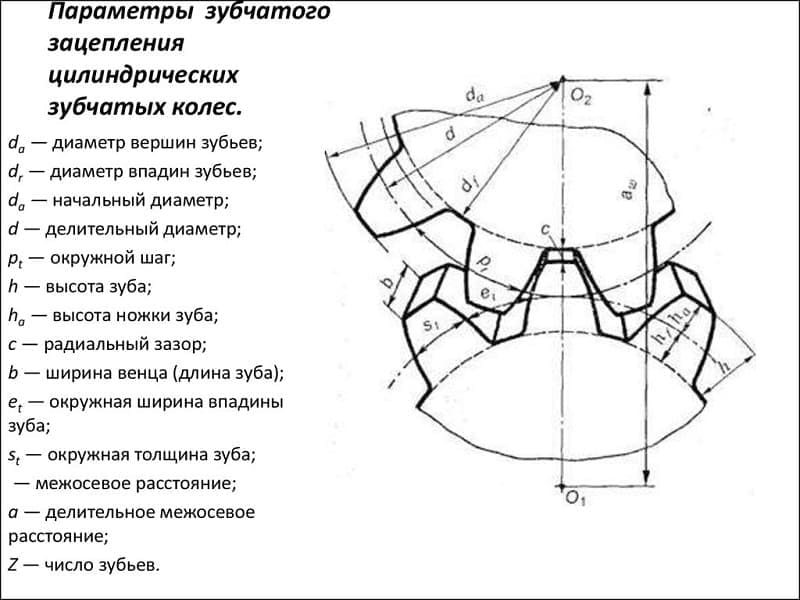
Если не учитывать основные параметры, то есть вероятность быстрого износа поверхности и появления многих других проблем.
Конструирование червячных колес и червяков.
Червяк. В большинстве случаев червяк делают за одно целое с валом; витки червяка могут быть получены фрезерованием, если do> df (рис. 1, а) или нарезаны на токарном станке, если do< df, т. е. имеется свободный выход резца (рис. 1, б).
Глобоидные червяки отличаются от цилиндрических формой участка нарезки (рис. 1, в); остальные элементы червяков этого типа конструируют так же, как и цилиндрические.
Червячное колесо. Для экономии цветных металлов червячное колесо выполняют составным: венец — из антифрикционного сплава (бронзы, латуни), центр — из стали или чугуна. Венец соединяется с центром по диаметру do посадкой с гарантированным натягом при dам2< 300 мм (рис. 2, а и б), болтами, поставленными без зазора, при dам2≥ 300 мм (рис. 2, в) или заливается центробежным способом (рис. 3). В первом случае для соединения обода и центра применяют посадки: Н7/p6, H7/r6 H7/s6 H7/s7 Н8/s7
Чтобы предотвратить взаимное окружное и осевое смещение венца и ступицы, по поверхностям разъема устанавливают винты (см. рис. 2, а). Иногда используют стандартные болты с шестигранной головкой (рис. 2, д), которые затягивают до упора.Рис. 1. Конструкция червяков: а — с фрезерованными витками; б — с витками, нарезанными на токарном станке; в — глобоидный Рис. 2. Конструкция червячных колес: а и б — с прессованным венцом; в — с привернутым венцом; г — цельное червячное колесо из чугуна; д — фиксация напрессованного венца болтом; δ 1= δ 2= 2m, но не менее 10 мм; dст= 1,6dв — для стальной ступицы; dст= 1,8dв — для чугунной ступицы; lст= (1,2…1,8)dв; диаметр винта dвнт= (1,2…1,5)m; длина винта lвнт= (0,3…0,4)b2; h = (0,15…0,2)b2; h = (0,15…0,2)b2; t = 0,1b2 Рис. 3. Венец, отлитый на чугунном колесном центре: а — с боковыми скосами; б — с прорезями; δ 1= δ 2= 2m, но не менее 10 мм; h = (0,3…0,5)b2; t = (0,3…0,4)h После затяжки лишнюю часть винтов (болтов) срезают, а оставшуюся во избежание отвинчивания закернивают в нескольких точках.
Посадочную поверхность выполняют с упорным буртиком или без него. Во избежание центрирования по двум поверхностям диаметр расточки в венце под буртик должен быть на 0,5… 1 мм больше диаметра центра колеса по буртику. Рекомендуемые размеры буртика: h = (0,15…0,2)b2, t = 0,1b2. В соединении без буртика винты ставят с двух сторон в шахматном порядке. Число винтов от трех до восьми с каждой стороны венца. Рекомендуемая толщина венца приведена ниже:
| Модуль m, мм Толщина венца δ 1 | 1,5 3,5m | 2,0 3,2m | 2,5 3m | 3,0 2,8m | 4,0 2,5m | 5,0 2,4m | ≥ 6,0 2,1m |
Диаметр винтов с dвнт= (1,2..1,5)m округляют по ГОСТ. Длина винтов lвнт= (2…3)dвнт. Толщину диска с принимают, как для цилиндрических колес.
Соединение по рис. 2 а, д ,проверяют на смятие по материалу венца при стальном колесном центре и по материалу колесного центра, если он выполнен из чугуна. Допустимое напряжение смятия см = 0,3σ т для бронзы и см = 0,4σ в.и для чугуна. При соединении, показанном на рис. 2, в, проверяют болты на срез ср = 0,25σ т и стенки отверстий на смятие см = 0,3σ т для бронзы, а при чугунном колесном центре см = 0,4σ в.и
При соединении венца с центром колеса отливкой в литейную форму заранее устанавливают центр колеса (см. рис. 3, a и б). Для гарантии против проворота венца на боковых поверхностях центра делают пазы, заполняемые металлом венца при его отливке. Форма обода для червячного колеса, выполняемого из чугуна без насадного венца, показана на рис. 2, г.
Технические характеристики
Редуктора отличаются внешне по размерам и форме. Внутреннее строение разнообразное. Объединяет их всех перечень технических характеристик, по которым они подбираются на различные машины и станки. К основным параметрам редуктора относятся:
- передаточное число;
- передаточное отношение;
- значение крутящего момента редуктора;
- расположение;
- количество ступеней;
- крутящий момент.
Передаточное число берется общее, всех передач, и одновременно указывается таблица передаточных чисел, если узел имеет 2 и более ступени. По нему подбирают узел, который преобразует вращение электродвигателя или мотора с нужное количество оборотов.

При этом важно знать величину крутящего момента на выходном валу редуктора, чтобы определить, будет ли достаточной мощность, чтобы привести в движение агрегат
Передаточное число
Основная характеристика зубчатого зацепления, по которой определяются все остальные параметры. Показывает, на сколько оборотов меньше делает колесо относительно шестерни. Формула передаточного отношения:
U = Z2/Z1;
где U – передаточное число;
Z1 число зубьев шестерни;
Z2 число зубьев зубчатого колеса.
Модуль зубьев шестерни и колеса одинаковый. Их количество напрямую зависит от диаметра. Поэтому можно использовать формулу:
U = D2/D1;
Где D2 и D1 диаметры колеса и шестерни соответственно.
Расчет общего передаточного момента определяется как произведение передаточных чисел всех пар:
Uр = U1× U2× … × Un;
Где Uр передаточное число;
U1, U2, Un передаточные числа зубчатых пар.
При расчете передаточного числа берется отношение количества зубьев колеса и заходов червяка.
В цепных передачах расчет передаточного числа делается аналогично, по количеству зубьев на звездочках и по диаметрам деталей.
При определении передаточного числа ременной пары количество зубьев заменяется диаметрами шкивов и все умножается на коэффициент скольжения. В отличие от зубчатой передачи, линейная скорость движения крайних точек на шкивах не равна друг другу. Зацепление не жесткое, ремень проскальзывает. КПД передачи ниже, чем у зубчатой и цепной передачи.
Передаточное отношение
При проектировании нового узла с заранее заданными характеристиками, за основу берется мощность будущего редуктора. Она определяется по величине крутящего момента:
где U12 – передаточное отношение;
W1 и W2 – угловые скорости;
n1 и n2 – частота вращения.
Знак «–» указывает на обратное направление вращения колеса и вала, на котором оно находится. При нечетном количестве передач ведомое колесо крутится в противоположном направлении по отношению к ведущему, навстречу ему. При четном количестве зацеплений конических колес вращение обоих валов происходит в одном направлении. Заставить его крутится в нужную сторону можно установкой промежуточной детали – паразитки. У нее количество зубьев как у шестерни. Паразитка изменяет только направление вращения. Все остальные характеристики остаются прежними.
Крутящий момент
Определение крутящего момента на валу необходимо, оно позволяет узнать мощность на выходе редуктора, величины связаны прямо пропорциональным соотношением.

Крутящий момент входного двигателя на входе, умножается на передаточное число. Для получения более точного фактического значения надо умножить на значение КПД. Коэффициент зависит от количества ступеней и типа зацепления. Для прямозубой конической пары он равен 98%.
Создаем 3D модель шестерни в программе Fusion 360.
Сейчас можно создать 3D модель для печати, на основании полученного эскиза. Для этого в программе Fusion 360 нажимаем на Sketch.
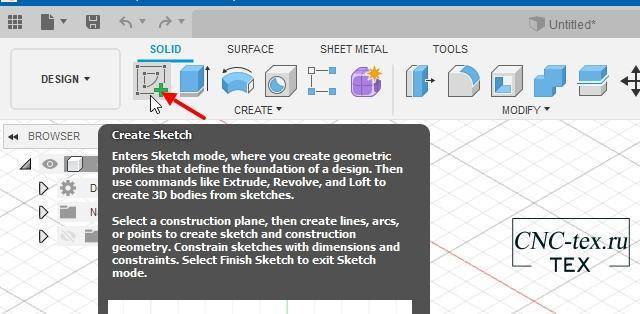
Выбираем плоскость, на которой будем создавать эскиз.
Затем в меню выбираем «Insert -> Insert SVG».

Нажимаем на кнопку загрузить с компьютера.

Выбираем файл, созданный в программе Inkscape.

Внимание, важный момент!!!! При загрузке создастся эскиз, но гораздо меньше. Необходимо рассчитать коэффициент увеличения. Иначе вы получите вот такой результат, оранжевые детали сделаны без коэффициента увеличения
Иначе вы получите вот такой результат, оранжевые детали сделаны без коэффициента увеличения.

Для расчета коэффициента, рисуем квадрат 100 на 100 мм. Загружаем в программу Fusion 360. Замеряем размер и 100 делим на полученное значение. У меня получился вот такой коэффициент: «3,795498538733063». Полностью значение можно не вводить. Но чем точнее значение, тем меньше будет отклонение в размере изделия. Я указал 3,795498.

Затем выделяем деталь и нажимаем кнопку экстрадировать. Выдавливаем деталь на 5 мм.

Вторую шестерёнку выдавливаем по аналогии.

Реечная передача в программе Fusion 360.
Если вы помните, мы не дорисовали реечную передачу в программе Inkscape. Поэтому нам нужно нарисовать её, для этого выбираем прямоугольник.
И рисуем по длине нашей рейки, нужной высоты.

Удаляем сторону прямоугольника, где у нас нарисованы зубцы рейки.

Затем экстрадируем полученную деталь.

В итоге получаем вот такой результат.

Как видим, все детали соединены точно так же, как и мы их нарисовали в программе Inkscape.
Чертеж – коническое зубчатое колесо
Чертеж – коническое зубчатое колесо
Чертежи конических зубчатых колес с прямолинейным профилем исходного контура выполняются по ГОСТ 2.405 – 75 в части указания параметров зубчатого венца и по другим стандартам ЕСКД.
Чертеж конического зубчатого колеса ( см. рис. 21) начинают тонкими линиями с проведения горизонтальной оси.
На чертежах конических зубчатых колес кроме размеров, определяющих форму и габариты детали, приводят размеры венца ( рис. 22.26, а, б): внешние диаметры dae и dae; угол 8а конуса вершин зубьев; угол 8 делительного конуса; угол ( 90 – 5) внешнего дополнительного конуса. Звездочкой обозначены размеры для справок.
На чертеже конического зубчатого колеса обозначают внешний диаметр вершин зубьев до притупления кромки dae и внешний диалгетр вершин зубьев после притупления кромки d ae, поскольку конус вершин зубьев и внешний делительный дополнительный конус на поверхности колеса не пересекаются. Наличие этой поверхности обусловлено тем, что часть цилиндрической поверхности заготовки длиной 1 х сохраняется при обработке по конусу вершин зубьев и внешнему делительному дополнительному конусу. Величину 1 х для мелкомодульных конических зубчатых колес принимают равной 0 1 мм.
На чертеже конического зубчатого колеса помещают таблицу параметров зубчатого венца, которая должна состоять из трех частей, отделенных друг от друга сплошными основными линиями: первая часть – основные данные; вторая – данные для контроля; третья – справочные данные.
На чертеже конического зубчатого колеса на изображении или в технических требованиях допускается приводить данные о форме, расположении и поведении зоны касания.
В какой последовательности выполняется чертеж конического зубчатого колеса.
В какой последовательности выполняют чертеж конического зубчатого колеса. Какие данные указывают на изображении конического зубчатого колеса.
Примеры простановки размеров на чертежах конических зубчатых колес приведены на фиг. Кроме основных значений, в штампе нужно указать еще и межосевой угол.
Пример указания параметров зубчатого венца на чертеже прямозубого конического зубчатого колеса со стандартным исходным контуром приведен на рис. 5.5. На чертеже помещается таблица параметров зубчатого венца, состоящая из трех частей, отделяемых сплошными основными линиями.
На рис. 16.44 приведен в качестве примера чертеж конического зубчатого колеса, из которого видно также и содержание таблицы для нарезания зубьев.
На рис. 268, в, г, д показана последовательность построения чертежа конического зубчатого колеса. Начинают с вычерчивания двух делительных конусов, имеющих общую образующую, нижний конус принадлежит колесу, верхний – сопряженной с ним шестерне.
Размеры толщины зуба s и высоты его головки hx по зубомеру ( рис. 149, а) определяют, зная модуль и число зубьев, используя соответствующие справочники, и проставляют в таблице параметров, обычно на чертежах конических зубчатых колес.
Страницы:
1
2
Как обозначается точность изготовления зубчатых колес
При изготовлении любые их виды имеют ряд погрешностей, среди которых выделяют четыре основные:
- кинематическую погрешность, связанную в основном с радиальным биением зубчатых венцов;
- погрешность плавности работы, вызываемую отклонениями шага и профиля зубьев;
- погрешность контакта зубьев в передаче, которая характеризует полноту прилегания их поверхностей в зацеплении;
- боковой зазор между неработающими поверхностями зубьев.
Для контроля первых трех погрешностей стандартами установлены специальные показатели – степени точности от 1 до 12, причем точность изготовления увеличивается с уменьшением показателя. Для контроля четвертой погрешности изготовления имеются два показателя:
- вид сопряжения зубчатых колес – обозначается литерами A, B, C, D, E, H;
- допуск на боковой зазор – обозначается литерами x, y, z, a, b, c, d, e, h.
Для обоих показателей бокового зазора обозначения даны в порядке убывания его величины и допуска на него.
Условно точность зубчатых колес обозначается двумя способами. Если степень точности по первым трем погрешностям одинакова, то ставится один общий для них численный показатель степени точности, за которыми стоят литеры обозначения вида сопряжения и допуска на боковой зазор. Например:
8-Ас ГОСТ 1643 – 81.
Если точности по первым трем погрешностям разные, то в обозначении ставятся три численных показателя последовательно. Например:
5-4-3-Са ГОСТ 1643 – 81.
Режем зубья любой формы
В реальных механизмах применяются шестеренки с различной формой поперечного сечения зуба: треугольной, эвольвентной, круговой и т.д. Далее мы рассмотрим способ, позволяющий создать контур шестеренки с зубьями любой формы.
Базовым элементом таких изображений является окружность. При помощи инструмента Эллипс (F7) создайте окружность нужного диаметра (рис. 17), удерживая нажатой клавишу Ctrl.

Рис. 17. Окружность — базовый элемент для создания изображения шестеренки
Рис. 18. Пиктограмма выбора режима Закругленный угол на панели свойств
Рис. 19. Скругление углов прямоугольника путем ввода числовых значений радиусов в поля на панели свойств
Теперь создайте заготовку зуба. В рассматриваемом примере он имеет форму трапеции со скругленными углами. При помощи инструмента Прямоугольник создайте прямоугольник. Скруглите верхние углы, выбрав режим Закругленный угол (рис. 18) и введя числовые значения радиуса в соответствующие поля на панели свойств (рис. 19). Для того чтобы нижние углы остались в исходном состоянии, отключите режим Изменить углы совместно (рис. 20).
Преобразуйте прямоугольник в кривую, нажав сочетание клавиш CtrlQ. При помощи инструмента Форма переместите правую и левую нижние узловые точки кривой на равные расстояния по горизонтальной оси по направлению от центра объекта, чтобы придать ему форму трапеции (рис. 21 и 22).
Рис. 20. Пиктограмма включения и отключения режима Изменить углы совместно на панели свойств
Рис. 21. Перемещение узловой точки кривой при помощи инструмента Форма
Рис. 22. Заготовка зуба готова
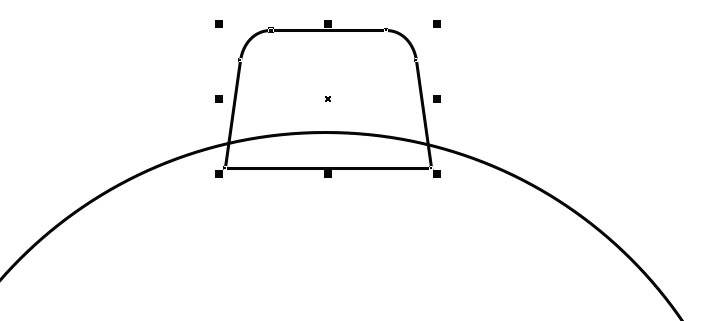
Рис. 23. Расположение заготовки зуба относительно окружности
Переключитесь на инструмент выделения и переместите модифицированный объект, как показано на рис. 23. Добавьте к выделению окружность и выровняйте объекты по вертикальной оси, выбрав в меню Объект -> Выровнять и распределить -> Выровнять центры по вертикали или нажав клавишу С
Обратите внимание на то, что оба нижних угла заготовки зуба должны находиться внутри окружности
Снимите выделение с группы, затем выделите заготовку зуба и щелкните по ней еще раз, чтобы перейти в режим вращения. Наведите курсор на маркер оси вращения и переместите его в центр окружности, ориентируясь по надписи «по центру» (рис. 24).

Рис. 24. Перемещение маркера оси вращения заготовки зуба в центр окружности

Рис. 25. Настройки раздела Вращение палитры Преобразования

Рис. 26. Заготовки зубьев равномерно распределены по окружности
Откройте раздел Вращение палитры Преобразования, выбрав в меню Окно -> Окна настройки -> Преобразования -> Повернуть или нажав сочетание клавиш AltF8. Чтобы рассчитать угол поворота, нужно разделить 360 на их количество. В приведенном примере оно равно 9. Соответственно, угол поворота составляет 40° (360/9=40). Количество копий должно быть на единицу меньше количества зубьев (в данном случае — 8).
Введите числовые значения угла поворота и количества копий в соответствующие поля палитры (рис. 25) и нажмите кнопку Применить. Заготовки зубьев равномерно распределены по окружности (рис. 26).
Выделите окружность и все заготовки зубьев. Объедините их в один объект, нажав кнопку Объединение на панели свойств (рис. 27). Выберите для созданного объекта заливку черного цвета и режим «без абриса». Контур шестеренки готов (рис. 28).

Рис. 27. Объединение группы выделенных объектов в один нажатием кнопки Объединение на панели свойств

Рис. 28. Контур шестеренки готов
В качестве тренировки попробуйте самостоятельно создать изображения шестеренок с зубьями другой формы.
Чертеж шестерни
Чертеж шестерни должен выполняться в соответствии с требованиями ЕСКД, содержать главный вид и всю необходимую информацию:
- диаметр вершин зубьев (внешний) до притупления кромки
- диаметр вершин зубьев (внешний) после притупления кромки
- расстояние от базовой до внешней плоскости окружности верхней кромки зубьев
- угол конусности зубьев
- угол дополнительного конуса
- ширина венца
- расстояние базовое
- радиусы кривизны и размеры фасок
- положение сечения
В правом углу чертежа, размещают таблицу, состоящую из трех частей, в которой указывают основные параметры:
- основные данные – верхняя часть
- контрольные данные – центральная часть
- справочные данные – нижняя часть
Справка:
Неиспользуемые строки в таблице исключаются или ставится прочерк.Подробнее о каждой величине прописано в ГОСТ 2.405-75.
Чертеж червячного колеса.
Шестерня.
Чертеж шестерни.
Конструктивное отличие зубчатых колес определяется:
- по геометрии зуба в поперечном сечении (форма) и способов контакта между собой: прямой – контактирует по точке; вогнутый – контактирует по линии; роликовый – контактирует с гребневым роликом.
- по типам колес: полное – когда оно постоянно вращается; сектор – когда оно поворачивается на определенный угол; сектор с роликом – когда рабочая длина контактируемого ролика уменьшена, по сравнению с контактируемой поверхностью глобоидального червяка.
Заказать чертеж
Документы
Шестерня m=4, Z=30
| Дата добавления: | 15.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 42.22 Кбайт |
| Скачиваний: | 974 |
Шестерня используется в станке 16А812.
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Шестерня m=4, Z=22
| Дата добавления: | 02.11.2010 |
| Дата изменения: | 02.11.2010 |
| Размер файла: | 36.1 Кбайт |
| Скачиваний: | 878 |
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Шестерня m=4, Z=21
| Дата добавления: | 28.05.2010 |
| Дата изменения: | 26.10.2010 |
| Размер файла: | 58.19 Кбайт |
| Скачиваний: | 911 |
Шестерня цилиндрическая прямозубая, m=4, Z=21, с посадкой на шлицы, зуб имеет затыловку, на ступице наружная резьба. Применяется в токарно – винторезном станке 1А64.
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Шестерня m=4, Z=17
| Дата добавления: | 03.11.2010 |
| Дата изменения: | 03.11.2010 |
| Размер файла: | 41.51 Кбайт |
| Скачиваний: | 842 |
Шестерня используется в станке ГФ2171
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Шестерня m=3.5, Z=16
| Дата добавления: | 09.06.2010 |
| Дата изменения: | 19.08.2010 |
| Размер файла: | 51.59 Кбайт |
| Скачиваний: | 860 |
Чертеж шестерни. Используется в станке 2Н57.
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Шестерня m=3, Z=60
| Дата добавления: | 01.11.2010 |
| Дата изменения: | 01.11.2010 |
| Размер файла: | 37.58 Кбайт |
| Скачиваний: | 883 |
Шестерня применяется в станке 2С163
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Шестерня m=3, Z=50
| Дата добавления: | 20.08.2010 |
| Дата изменения: | 20.08.2010 |
| Размер файла: | 42.49 Кбайт |
| Скачиваний: | 938 |
Шестерня m=3, Z=50 используется в станке 2С550
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Шестерня m=3, Z=50
| Дата добавления: | 01.11.2010 |
| Дата изменения: | 01.11.2010 |
| Размер файла: | 40.79 Кбайт |
| Скачиваний: | 876 |
Шестерня применяется в станке 2С163
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Шестерня m=3, Z=42
| Дата добавления: | 03.06.2010 |
| Дата изменения: | 22.06.2010 |
| Размер файла: | 50.13 Кбайт |
| Скачиваний: | 870 |
Чертеж шестерни цилиндрической с посадкой на шпонку. Применяется в станке 1М63ДФ101.
Чертежи выполнены в двух форматахcdw – Компас 9 СП2dwg – Autocad 2000
Спироидные зубчатые передачи

Спироидные зубчатые передачи
Спироидные зубчатые передачи — это гипоидные зубчатые передачи, в которых начальные поверхности зубчатых колёс конические, шестерни имеют винтовые зубья, а зубчатые колеса имеют сопряженные поверхности зубьев с линейным контактом, если производящая поверхность для одного из них совпадает с главной поверхностью зубьев первого зубчатого колеса. По форме поверхности вершин витков червяка и способу его расположения относительно межосевой линии их разделяют на три вида: цилиндрические спироидные передачи, традиционно конусные наружного зацепления, обратноконусные внутреннего зацепления (рис. 8).
Выполнение чертежа конической зубчатой передачи
Два конических зубчатых колеса, находящиеся в зацеплении, должны иметь одинаковый модуль зацепления. Как уже было сказано выше, большинство конических зубчатых передач, применяемых в современных машинах и станках, имеют оси валов, пересекающиеся под углом 90°, и общую вершину начальных конусов.
Ниже (фиг. 539) разобрано выполнение чертежа такой передачи. Для его выполнения необходимо знать диаметры начальных окружностей, количество и длину зубьев колес, конструкцию колес и их размеры. При выполнении чертежа по заданным модулю m и числу z1 зубьев первого колеса и числу z2 второго колеса определяем диаметры начальных окружностей:1) для первого колеса d 1 = mz12) для второго колеса d2 = mz2
Зная диаметры d1 и d2, приступаем к выполнению чертежа.
Построение конической зубчатой передачи
Построение (фиг. 539). Дано: модуль зацепления m, числа зубьев z1 первого колеса и z2 второго колеса. Требуется вычертить коническую зубчатую передачу.
1. Определяем необходимые данные, затем строим проекции начальных конусов:а) в плоскости П2 строим штрих – пунктирными линиями прямой угол и от вершины его А откладываем влево диаметр d1 а вверх диаметр d2, через их середины проводим перпендикулярные к ним линии – оси колес, точку пересечения осей, которая явится вершиной начальных конусов, обозначим S и соединим ее штрих – пунктирными линиями с концами диаметров начальных окружностей.б) переносим все характерные точки построения на плоскость П
3 и изображаем штрих-пунктирными линиями начальные конусы.
2. Приняв за основу диаметр d2 вычерчиваем большое зубчатое коническое колесо, в данном случае согласно указаниям к фигуре №536.
3. Приняв за основу диаметр d1 вычерчиваем малое зубчатое колесо. На данном чертеже его конструктивная форма несколько отличается от формы первого колеса, но основы построения остаются такими же, как и для первого.
4. Для выявления на чертеже ведущего колеса очертание его зуба в месте зацепления следует обвести сплошными линиями, а внешнюю линию очертания зуба большого колеса – штриховой линией. Удаляем вспомогательные линии; заштриховываем изображения разрезанных поверхностей обоих колес: первого в одну сторону, а второго – в другую. Наносим все необходимые размеры.
Зубчатые передачи….
Коническая зубчатая передача….
Чертеж цилиндрической зубчатой передачи…..
Машиностроительное черчение детали…..
Червячная передача…..
Конструкция и параметры зубчатого колеса
Оно содержит венец с зубьями, диск и ступицу. Имеется три наиболее важных его параметра: модуль, диаметр делительной окружности и количество зубьев. Какую же делительную окружность имеет зубчатое колесо? Чертеж цилиндрического колеса с типовыми эвольвентными зубьями показан ниже.

pmd m = d/z= p/3,14, мм.
Например, зубчатое колесо с 22 зубьями и диаметром 44 мм имеет модуль m = 2 мм. Сцепленные шестерни должны обе иметь один модуль. Значения их стандартизованы, и как раз на делительной окружности модуль данного колеса принимает свое стандартное значение.
Высота головки зуба одного колеса меньше высоты ножки зуба второго, зацепляющегося с ним, благодаря чему образуется радиальный зазор c.
Для обеспечения бокового зазора δ между двумя сцепленными зубьями сумма их толщин принимается меньше их окружного шага p. Радиальный и боковой зазоры предусматриваются для создания необходимых условий смазки, нормальной работы передачи при неизбежных неточностях изготовления и сборки, тепловом увеличении размеров передачи и т. п.
9.7. Выполнение чертежа детали, изготовленной литьем, с последующей механической обработкой
Формообразование литьем позволяет получить достаточно сложную форму детали, практически без потерь материала. Но после литья поверхность получается достаточно грубая, поэтому, рабочие поверхности требуют дополнительной механической обработки.
Таким образом получаем две группы поверхностей — литейные (черные) и обработанные после литья (чистые).Процесс литья: в литейную форму заливается расплавленный материал, после остывания заготовка вынимается из формы, для чего, большинство поверхностей заготовки имеют литейные уклоны, а сопряжения поверхностей — литейные радиусы скруглений.
Литейные уклоны можно не изображать, а литейные радиусы должны быть изображены обязательно. Размеры литейных радиусов скруглений указывают в технических требованиях чертежа записью, например: Неуказанные литейные радиусы 1,5 мм.
Основная особенность нанесения размеров: так как есть две группы поверхностей, то есть и две группы размеров, одна связывает все черные поверхности, другая — все чистые, и по каждому координатному направлению допускается проставлять только один размер, связывающий между собой эти две группы размеров.
На рисунке 9.12 такими размерами являются: на главном изображении — размер высоты крышки — 70, на виде сверху — размер 10 (от нижнего торца детали) (выделены синим цветом).
При литье применяют литейный материал (буква Л в обозначении), обладающий повышенной текучестью, например:
- стали по ГОСТ 977-88 (Сталь 15Л ГОСТ 977-88)
- серые чугуны по ГОСТ 1412-85 (СЧ 15 ГОСТ 1412-85)
- литейные латуни по ГОСТ 17711-93 (ЛЦ40Мц1,5 ГОСТ 17711-93)
- алюминиевые сплавы по ГОСТ 2685-75 (АЛ2 ГОСТ 2685-75)
Рисунок 9.12 — Чертеж литейной детали
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
Для более крупных потребуются измерения и вычисления.
Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
m=De/(z+2)
Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.
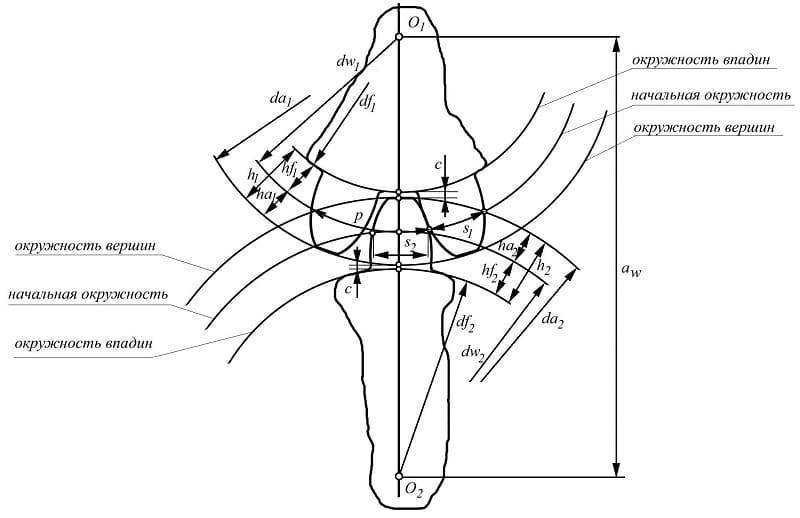
Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.